 |
#1 - 19-02-2012 18:16:01
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3534
- Lieu: 94110
Fromage u dessert ?
Finalement, ce sera fromage.
Je suis allé chez mon pâtissier, mais comme il n'avait pas de gâteau à mon goût, je me suis rendu chez mon fromager.
Là, j'ai aperçu un magnifique Brie de Meaux parfaitement circulaire et de hauteur constante (de 2,8 kg pour un diamètre d de 36 cm).
Voyant mon intérêt, mon fromager voulait me le vendre en entier ! Mais je lui dis :
" - Vas-y molo ! Je me contenterai d'un quart  . .
- Pas de problème."
Et en deux coups de couteaux rectilignes bien placés, il m'en a découpé une part d'exactement 700 g, mais dont la forme m'a un peu étonné car les deux traits de coupe ne se rejoignaient pas au centre du fromage.
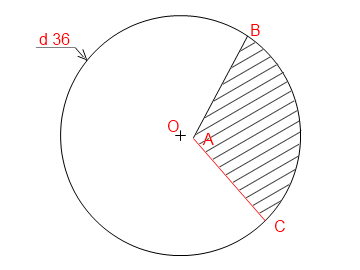
Comme je lui demandais la raison de cette découpe un peu particulière, il m'a expliqué qu'il tenait à ce que, pour des raisons de conservation, la surface de la découpe sur la partie non encore vendue, soit la plus petite possible.
Pourriez-vous préciser les formes et dimensions en fonction de rayon r de ce fromage entamé ?
La case réponse valide le rapport entre la longueur de découpe et le diamètre d, arrondi au plus proche avec un "0", un point décimal et 4 chiffres derrière la virgule.
#2 - 19-02-2012 20:10:26
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
Fomage ou dessert ?
Je ne trouve pas pareil que la case réponse 
Je trouve en effet que pour minimiser la longueur des 2 segments de découpe (que j'ai supposés égaux), il faut qu'ils soient alignés.
Du coup, la valeur de l'angle BOC est la racine de l'équation :
x−sinx=π2
Et le rapport demandé vaut : sinx2
Et je trouve la valeur approchée : 0,9147710175730....
J'ai également à ma dispo le rapport en fonction de cet angle BOC, mais la formule est vraiment horrible !
#3 - 19-02-2012 22:08:58
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3534
- Lieu: 94110
fromzge ou dessert ?
LOOping : C'est mieux que la découpe classique  , mais on peut faire nettement mieux que cette configuration , mais on peut faire nettement mieux que cette configuration  . .
#4 - 19-02-2012 23:44:21
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Fromag ou dessert ?
0.8874 en partant du principe que les deux coupes ont même longueur.
Merci à toi pour l'énigme et à WA pour m'avoir permis d'arriver au bout 
#5 - 20-02-2012 09:38:22
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Fromaage ou dessert ?
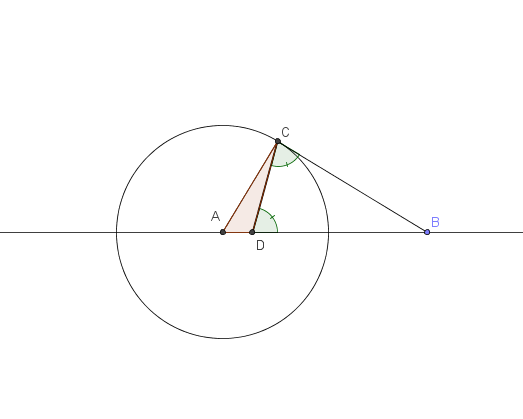
Pour réduire la longueur de la coupe, il faut que les deux angles soient égaux.
La surface découpée est égale à 2 fois (secteur moins triangle hachuré).
L'équation peut se résoudre par WolframAlpha ou graphiquement avec Geogebra.
Cela conduit à un rapport de 0.887438...
On peut encore réduire ce rapport avec une autre méthode de coupe.
#6 - 20-02-2012 13:39:00
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Fromage ou dessert
Est-ce le fromage est bombé au milieu, ou est-il parfaitement cylindrique?
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#7 - 20-02-2012 13:41:42
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3236
- Lieu: Luxembourg
fromage ou dessery ?
Bonjour,
J'ai d'abord cru que Jackv voulait se lancer dans la pâtisserie, mais son clin d'oeil à Vasimolo m'a rassuré: dans la bande P2T, nous avons maintenant un pâtissier et un fromager: 
Je considère (sans être capable de le prouver rigoureusement) que la découpe est symétrique (c'est à dire que la droite OA est aussi la bissectrice de l'angle BC).
On cherche à avoir un quart du cercle total ou, ce qui revient au même, à couper un quart de cercle en deux parties de surfaces égales.
Mon segment de découpe (en fait de demi-découpe) part d'un point de l'axe des abscisses (d'abscisse x) et arrive à un point du quart de cercle (d'angle a avec Ox).
On aura: a/2 - x sina/2 = pi/8, d'où: x = (a-pi/4)/sina
Je cherche donc à optimiser le carré (plus facile) de la distance entre ces deux points:
f(a) = sin²a + [cosa - (a-pi/4)/sina]²
f'(a) = [(a-pi/4)cosa - sina - sin²a].[(a-pi/4)cosa - sina + sin²a].sin³a/cosa
(c'est la version simplifiée: je vous ai fait grâce des détails de calcul).
Je cherche alors à annuler cette dérivée, soit: (a-pi/4)cosa - sina + sin²a = 0
J'ai utilisé un tableur, qui me donne: a=1,02471 puis x=0,28004 et enfin la valeur cherchée [f(a)]^(1/2) = 0,8874 validée par la case réponse.
J'ai conscience que ma solution est peu élégante, mais je n'en ai pas trouvé d'autre. Attendons voir comment ce problème a été appréhendé.
Bonne journée à tous.
Frank
#8 - 20-02-2012 13:59:20
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
fromage ou drssert ?
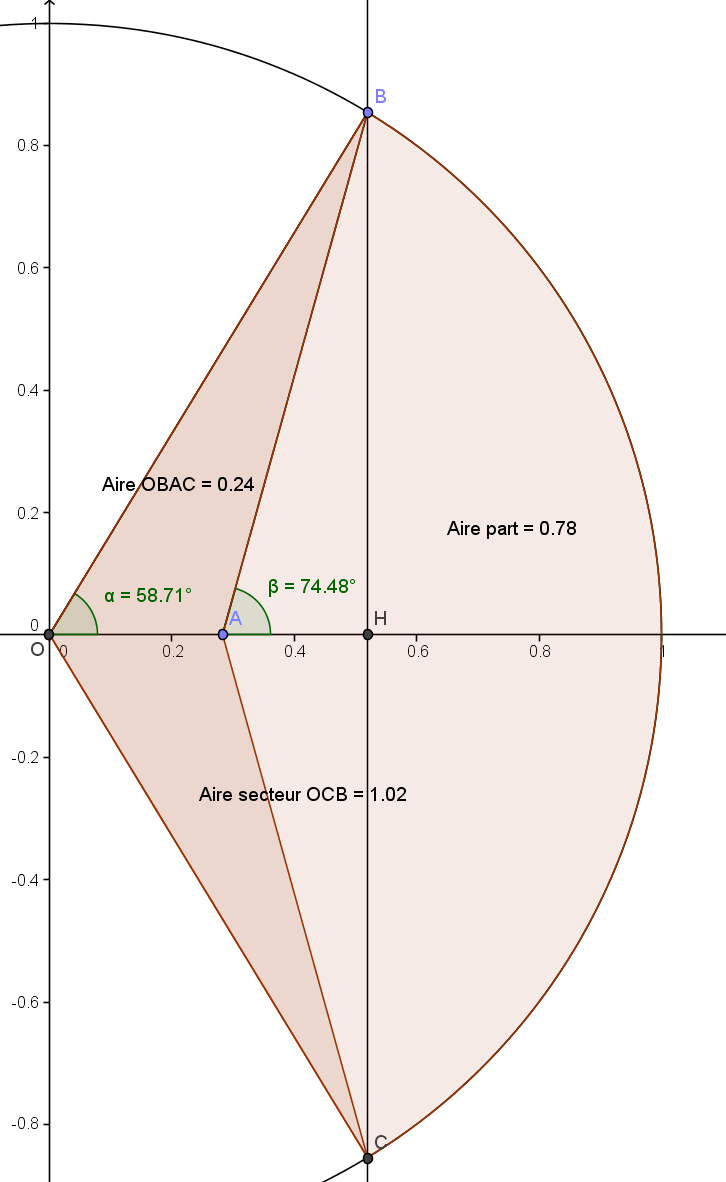
Notons H le milieu du segment [BC]. La droite (OH) est la médiatrice du segment [BC].
Tout d'abord, voyons pourquoi A doit se situer sur cette médiatrice (OH) pour optimiser la longueur de coupe AB+AC, une fois que B et C sont fixés :
On considère la droite d parallèle à la droite (BC) et passant par le point A.
On appelle C' le symétrique orthogonal du point C par rapport à cette droite d.
En se restreignant à optimiser sur cette droite d, on constate que l'on cherche à optimiser BA+AC', or le plus court chemin entre deux points étant la ligne droite, le minimum sera atteint lorsque A est aligné avec B et C', c'est-à-dire lorsque A est le milieu de [BC']. On considère donc pour la suite que A se situe sur la droite (OH).
On note α l'angle HOB, β l'angle HAB.
Pour une coupe optimisée, A doit se situer entre O et H.
Pour simplifier, on prend le rayon du cercle égal à 1.
L'aire de la surface hachurée peut se calculer en soustrayant l'aire des triangles OAB et OAC (de base OA et hauteur BH) à l'aire du secteur circulaire BOC (d'angle 2α).
Elle est égale à : α−OA×BH
Cette surface doit faire le quart du disque, ce qui donne la contrainte :
\frac{\pi}{4}=\alpha - OA \times BH[/latex]. Notre but est de minimiser la longueur de coupe AB sous cette contrainte. Un peu de trigonométrie : [latex]sin\alpha = BH
cos\alpha = OH
sin\beta = BH/AB
cos\beta = AH/AB
On en tire que AB=\frac{sin\alpha}{sin\beta}
AH = AB cos\beta
OA = OH - AH = cos\alpha - AB cos\beta = cos\alpha - \frac{sin\alpha}{sin\beta}cos\beta = cos\alpha - \frac{sin\alpha}{tan\beta}
La contrainte peut s'écrire \frac{\pi}{4}=\alpha - \left(cos\alpha - \frac{sin\alpha}{tan\beta}\right) sin\alpha.
On en tire que tan\beta = \frac{sin^2\alpha}{sin\alpha cos\alpha - \alpha +\pi/4}
et finalement :
AB = \frac{sin\alpha}{sin\left(arctan\left(\frac{sin^2\alpha}{sin\alpha cos\alpha - \alpha +\pi/4}\right)\right)}
Un coup de Wolfram Alpha nous dit que le minimum pour AB est \simeq 0.8874, atteint lorsque \alpha \simeq 58°71
#9 - 20-02-2012 15:34:36
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3534
- Lieu: 94110
#10 - 20-02-2012 18:50:46
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3834
fromage oi dessert ?
Petite observation: si on voulait obtenir une longueur min de découpe, ce ne serait sans doute pas des segments de droite, mais une courbe.
#11 - 21-02-2012 17:05:50
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
frpmage ou dessert ?
Petite précision : La découpe doit se faire par 2 coups de couteau rectilignes ou pas forcément ?
#12 - 21-02-2012 18:14:07
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3534
- Lieu: 94110
fromage iu dessert ?
Une petite précision complémentaire : les découpes au couteau sont rectilignes.
#13 - 21-02-2012 21:30:15
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3236
- Lieu: Luxembourg
fromage ou fessert ?
Une découpe lenticulaire (hors sujet ici) sera effectivement plus optimale qu'une découpe rectiligne. Proposons la à ton fromager. 
#14 - 22-02-2012 13:34:44
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
fromagr ou dessert ?
Je trouve une distance OA de 4.9741383cm
un angle BOC de 117 degrés exactement
un rapport entre la longueur de découpe et le diamètre D de 0.887462
Egalement, B & C sont symmetriques par rapport a la ligne qui passe par O et A.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#15 - 22-02-2012 14:36:24
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3534
- Lieu: 94110
Fromage ou desset ?
dhrm : Bravo ! le rapport que tu obtiens est très proche de mon résultat  (bien que ta valeur de OA s'éloigne de plus de 1 % de ma valeur, confirmée par ailleurs) (bien que ta valeur de OA s'éloigne de plus de 1 % de ma valeur, confirmée par ailleurs)  . .
nodgim et Franky : Sous la pression, je me résouts à mettre en ligne le second épisode de mes aventures fromagères :
http://www.prise2tete.fr/forum/viewtopi … 32#p140754
#16 - 22-02-2012 19:40:56
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
Fromagee ou dessert ?
J'ai refait mes calculs, et je trouve une équation complètement différente ... mais qui tombe juste cette fois !
En appelant \alpha la moitié de l'angle BOC, j'exprime le rapport cherché en fonction de \alpha, et ensuite c'est Wolfram qui fait le reste !
r(\alpha)=\sqrt{\sin ^2\alpha+\left(\frac{\frac{\pi}4-\alpha+\frac{\sin(2\alpha)}2}{\sin \alpha}\right)^2}
Et Wolfram me dit que le minimum atteint vaut r_{min} \approx 0.8874, avec \alpha_{min} \approx 58,7^{\circ}
Pour obtenir cette formule, je passe par les aires : du triangle ABC, du triangle ABC, et du cornet de glace OBC. J'ai également supposé AB=AC. Sinon, cela rajoute une variable supplémentaire, mais la recherche du minimum impose ensuite l'égalité des 2 longueurs.
#17 - 23-02-2012 12:22:27
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Fromage ou desseert ?
J'avais fait une petite erreur. J'ai recalculé, et maintenant:
Je trouve une distance OA de 5.0406857cm
un angle BOC de 117.422919 degrés
un rapport entre la longueur de découpe et le diamètre D de 0.8874383
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#18 - 23-02-2012 17:14:26
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3534
- Lieu: 94110
Fromage ou edssert ?
LOOping et dhrm : on est maintenant parfaitement d'accord  ! !
#19 - 24-02-2012 00:56:04
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Fromage ou dssert ?
Une petite réponse ne serait-ce que pour remercier Jackv pour le clin d’œil à mon pâtissier 
J'ai fait tout les calculs et je suis arrivé au même résultat que vous . Après il fallait sortir la grosse l'artillerie et là le pâtissier il aime pas trop . Il préfère malaxer et ciseler la pâte à la main .
Ceci dit ces problèmes qui culbutent les pseudos-évidences sont toujours très intéressants .
Vasimolo
#20 - 24-02-2012 01:21:16
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Fromage o dessert ?
halloduda, tu peux expliquer un peu ?
#21 - 24-02-2012 11:04:09
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3534
- Lieu: 94110
Fromagee ou dessert ?
Tout d'abord, merci à Vasimolo et à son pâtissier  pour l'inspiration du style de cette énigme ! pour l'inspiration du style de cette énigme !
La découpe doit elle être nécessairement symétrique ? Si j'ai fait l'optimisation pour le quart d'un demi-fromage, il me parait évident que si je recommence ensuite la même opération pour l'autre moitié, j'obtiendrai un résultat comparable ; la découpe doit donc être symétrique.
J'ai donc choisi de m'intéresser à un demi-fromage et de paramétrer les dimensions de la découpe en fonction de l'angle DOB = \alpha, en considérant que le rayon est de longueur unité.
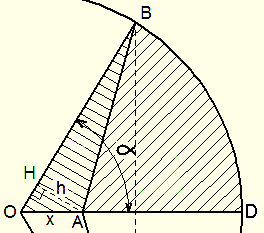
L'aire du secteur ODB a comme valeur \alpha/2.
On souhaite que ADBA ait une aire égale à \pi/8.
Le triangle OAB a donc une aire de \alpha/2 - \pi/8
et sa hauteur AH = h = 2*(\alpha/2 - \pi/8),
soit h = \alpha - \pi/4
La distance OA = x = h/sin (\alpha)
et la longueur AB = \sqrt (1+x² - 2*x*cos(\alpha)) ,
valeur qu'il reste à minimiser.
Personnellement, je n'ai même pas développé l'écriture de cette fonction, et encore moins cherché à la dériver.
N'étant pas adepte de Wolfram Alpha, je me suis contenter d'utiliser un tableur et j'obtiens :
AB = 0.887438320
pour a = 58.7115 ° = 1.024709 rd
avec h= 0.23931
et x = 0.280039
Je ne sais pas si ma solution est la plus élégante, mais j’apprécie la diversité de toutes celles proposées.
Bravo  et merci à tous ceux qui ont planché sur ce problème. et merci à tous ceux qui ont planché sur ce problème.
Je suis bien conscient que l'on peut faire mieux pour optimiser cette longueur si on ne s'en tient pas à une découpe rectiligne.
C'est pourquoi j'invite ceux qui ne l'auraient pas encore fait à rendre une nouvelle visite à mon fromager :
http://www.prise2tete.fr/forum/viewtopi … 32#p140754
halloduda : ta remarque sur l'égalité des angles est très judicieuse  , mais il est vrai que le développement de l'ensemble est une peu succinct ... , mais il est vrai que le développement de l'ensemble est une peu succinct ...
#22 - 24-02-2012 14:51:15
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Fromage ou dessret ?
Jackv, selon moi, tu ne démontres en rien que la découpe optimale est symétrique.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum










