Je sèche...

Le principe pourrait être, comme dans l'énigme à laquelle tu fais référence Vasimolo, de

(A) grouper d'un côté les fils dans des groupes de tailles différentes. A_1,...,A_n

(B) grouper de l'autre côté les fils dans des groupes de tailles différentes contenant au plus un fil de chacun des groupes de l'étape A. (B_1...B_n)

(C) revenir et identifier les fils (l'intersection de A_j et B_i contient au plus un fil)

Ça marche pour N=n(n+1)/2 (n groupes de n tailles différentes)

Par contre, pour N=5, par exemple, je ne vois pas comment faire les groupements. (d'abord deux groupes 3-2 puis trois groupes 1-2-2 ? Mais comment distinguer les deux groupes de 2 ?)

Il le branche a un fil, il attend, puis il le branche a un autre fil. Après il va a l'extrimité et il verra quel fil est chaud, et ou il se prend 1 decharge.

Pour n fils avec n = k(k+1)/2
Il fait 1 paquet de 1, 1 paquet de 2, ... un paquet de k fils notés P1, P2, ... Pk
De l'autre côté, il peut identifier les fils par paquets: Q1 = A1, Q2 = P2 (sans pouvoir distinguer les deux fils pour l'instant), ... Qk = PK (sans pouvoir distinguer les k fils pour l'instant)
Il regroupe ensuite les fils en paquets P': P'1 avec un fil de Qk, P'2 avec un fil de Qk et un fil de Qk-1, ... P'k avec un fil de Qk, un fil de Qk-1, ... un fil de Q1
De l'autre côté, il peut identifier les fils par paquets: Q'1 = P'1, Q'2 = P'2 ...
Un fil dans un groupe Px et dans un autre groupe Q'y correspond de l'autre côté au fil de Qx qu'on a mis dans le groupe P'y.

Ca c'est pour n=k(k+1)/2

Pour n != k(k+1)/2, on a quoi ?
- 4 fils: notés A1, B1, B2 et C1; B1 et B2 reliés
De l'autre côté, on identifie le groupe B ainsi que deux fils "A ou C".
On laisse le 1er "A ou C" tout seul, on relier un des fils de B à l'autre "A ou C", et on laisse l'autre B seul.
De l'autre côté, on peut identifier un B seul, ainsi que A seul ou C seul, ce qui permet de savoir lequel seul de l'autre côté, le B qui reste et le A ou C qui restent sont normalement regroupés (mais bon on s'en fout)

- 5 fils:
A1, B1, B2, C1 et C2 (la première lettre indique le groupe)
De l'autre côté, on identifie A1, ainsi que P1, P2 et Q1, Q2 (P peut correspondre à B ou à C, et inversement pour Q)
On laisse P1 seul, on relie P2 et Q1, on relie A1 et Q2
De l'autre côté, on cherche quel fil fait groupe avec A1. Il correspond à Q2 de l'autre côté. Si c'est un B, alors Q = B, sinon Q = C. L'autre groupe de 2 nous permet de distinguer Q1 et P2 (et on sait déjà si Q=B ou Q=C) et le dernier fils seul correspond à P1.

- 7 fils
A1, B1, B2, C1, C2, C3, D1
De l'autre côté, on identifie 2 fils seuls (A1 ou D1) notés P1 et Q1, ainsi que B'1, B'2 et C'1, C'2, C'3
On relie P1, B'1 et C'1; on relie B'2 et C'2; on laisse C'3 et Q1 seuls
De l'autre côté, A ou D doit être seul, ce qui permet d'identifier Q1 (celui qui est seul) et donc P1 (l'autre). Un autre fil est seul dans le groupe C: C'3. Le groupe de 3 contient P1 (identifié), un fil de B (B'1) et un fil de C (C'1). Le B restant est relié à B'2 et le C restant à C'2

- 8 fils
A1, B1, B2, C1, C2, C3, D1, D2
De l'autre côté: on trouve A1, on trouve C'1, C'2 et C'3; on trouve aussi P1, P2 et Q1, Q2 sans savoir si P=B ou si P=D
On laisse C'3 seul, on groupe C'2 et P1, on groupe C'1, Q2 et A1, on groupe P2 et Q1
De l'autre côté: le groupe de 3 nous donne un fil dans C (C'1), A1 et un fil dans D ou dans B (Q2) qui nous permet en plus d'identifier P et Q par rapport à B et D. Du coup les deux fils de B et D reliés nous donnent P2 et Q1, et l'autre groupe de 2 nous donne C'2 et P1, le dernier fil est le C'3 seul

- pour 9 fils:
A1, B1, B2, C1, C2, C3, D1, D2, D3
De l'autre côté, on identifie A1 (seul), B'1, B'2, P1, P2, P3, Q1, Q2 et Q3 avec P=C ou D et inversement pour Q
On laisse Q3 seul, on relie Q2 et P3, on relie Q1, P2 et B'2, on relie P1, B'1 et A1
De l'autre côté, le fil seul correspond à Q3 et permet d'identifier P et Q, le groupe de 2 fils permet d'identifier Q2 et P3, le groupe de 3 qui ne contient pas A1 permet d'identifier Q1, P2 et B'2, 1 des fils restants est A1, l'autre est dans B et donc lié à B'1, le dernier à P1.

Je sais pas si j'arriverai à généraliser formellement, mais bon par rapport au cas (k)(k+1)/2, on a deux groupes avec le même nombre de fils. En laissant un seul de ceux là seul de l'autre côté, on peut identifier et distinguer ces deux groupes.

Une bonne réponse de scarta qui n'a pas utilisé la même méthode que moi

Pour ceux qui doutent ou qui cherchent encore , un exemple avec 4 fils :



On numérote les fils  1 , 2 , 3 et 4 et on lie ensemble 3 et 4 . On passe de l'autre côté et on repère facilement les fils rouges et bleus ( mais sans distinguer le 1 du 2 ou le 3 du 4 ) . On numérote A et B les deux fils rouges et C et D les bleus avant de nouer B et C et de revenir au point de départ :

Si 1 est relié à quelqu'un alors 1 est B sinon 1 est A .
Si 1 est A alors 2 est B et si 1 est B alors 2 est A .
Si 3 est relié à quelqu'un alors 3 est C sinon 3 est D
Si 3 est C alors 4 est D et 3 est D alors 4 est C .

Ca fait un peu mal à la tête mais on finit par si faire .

Bonne continuation .

Vasimolo

Considérons une entier [latex]n[/latex] plus grand que 2.
On pourra toujours l'écrire de la façon suivante:
[TeX]n=1+2+...+(p-1)+p+k[/latex] avec [latex](p,k)\in\mathbb{N}^2\backslash p\ge 2, k\le p[/TeX]
Pour [latex]k=0[/latex], le problème a déjà été traité dans ton autre énigme, on sait qu'il y a une solution. Dans la suite, on supposera [latex]k>0[/latex] pour simplifier.

Je propose alors de repérer les fils dès la première étape avec [latex]p[/latex] couleurs et de les séparer en [latex](p+1)[/latex] groupes de façon à ce qu'il y ait [latex](p-1)[/latex] groupes, parmi lesquels chacun a un une couleur et un nombre de fils différent de celui des autres, et deux groupes de même couleur et de [latex]k[/latex] fils.
Des exemples:
[latex]4 =1+2+1=\overbrace{1+1}+2[/latex], 3 groupes, 2 couleurs
[latex]5 =1+2+2=1+\overbrace{2+2}[/latex], 3 groupes, 2 couleurs
[latex]7 =1+2+3+1=\overbrace{1+1}+2+3[/latex], 4 groupes, 3 couleurs
[latex]8 =1+2+3+2=1+\overbrace{2+2}+3[/latex], 4 groupes, 3 couleurs
[latex]9 =1+2+3+3=1+2+\overbrace{3+3}[/latex], 4 groupes, 3 couleurs
[latex]11=1+2+3+4+1=\overbrace{1+1}+2+3+4[/latex], 5 groupes, 4 couleurs
...

Etape 1: On lie tous les fils de chaque groupe ensemble (on forme [latex](p+1)[/latex] groupes). Puis on assigne à chaque groupe, une couleur suivant le nombre de fils qu'il contient (soit [latex]p[/latex] couleurs au total). Disons que l'on réserve la couleur rouge pour les deux paquets de [latex]k[/latex] fils. On range chaque groupe de gauche à droite par ordre croissant de leur nombre de fils.

Etape 2: De l'autre coté, donc. On est capable de reformer [latex](p-1)[/latex] groupes et de leur assigner leur couleur. Il reste deux groupes de [latex]k[/latex] fils de couleur rouge. On range également de gauche à droite, tous les groupes par ordre croissant de leur nombre de fils.
L'astuce consiste à faire en sorte qu'à l'étape suivante, on puisse faire la distinction entre ces deux paquets. Pour cela, on prend un fil du paquets rouge le plus à gauche que l'on lie avec un fil du paquet discernable qui en compte le plus si [latex]k<p[/latex] ou qui en compte le moins si [latex]k=p[/latex] (lien en pointillés sur le schéma du dessous). On choisit de garder la couleur rouge pour ce paquet indiscernable. On réserve le vert pour l'autre paquet indiscernable.
Enfin, on prend le paquet qui a le plus de fils, et on lie chacun d'eux avec un fil des paquets qui le précèdent (qui ont au fur et à mesure, de moins en moins de fils), tout en gardant à l'esprit que si [latex]k<p[/latex], aucun fil vert ne doit être relié au plus grand paquet discernable. On s'arrête quand il reste un fil, si c'est possible. Puis, on procède de la même façon pour tous les paquets qui le précèdent (à sa gauche).

Etape 3: Au point de départ donc. On commence par enlever les liens de l'étape 1, puis on fait la distinction entre les deux paquets rouges. Celui qu'on a gardé rouge, sera celui qui sera connecté à un fil du plus grand paquet discernable (lien en pointillés). L'autre, sera donc le vert. Puis le reste suit en lisant le diagramme que l'on aura pris soin de noté au cours des étapes précédentes et dont voici quelques exemples...


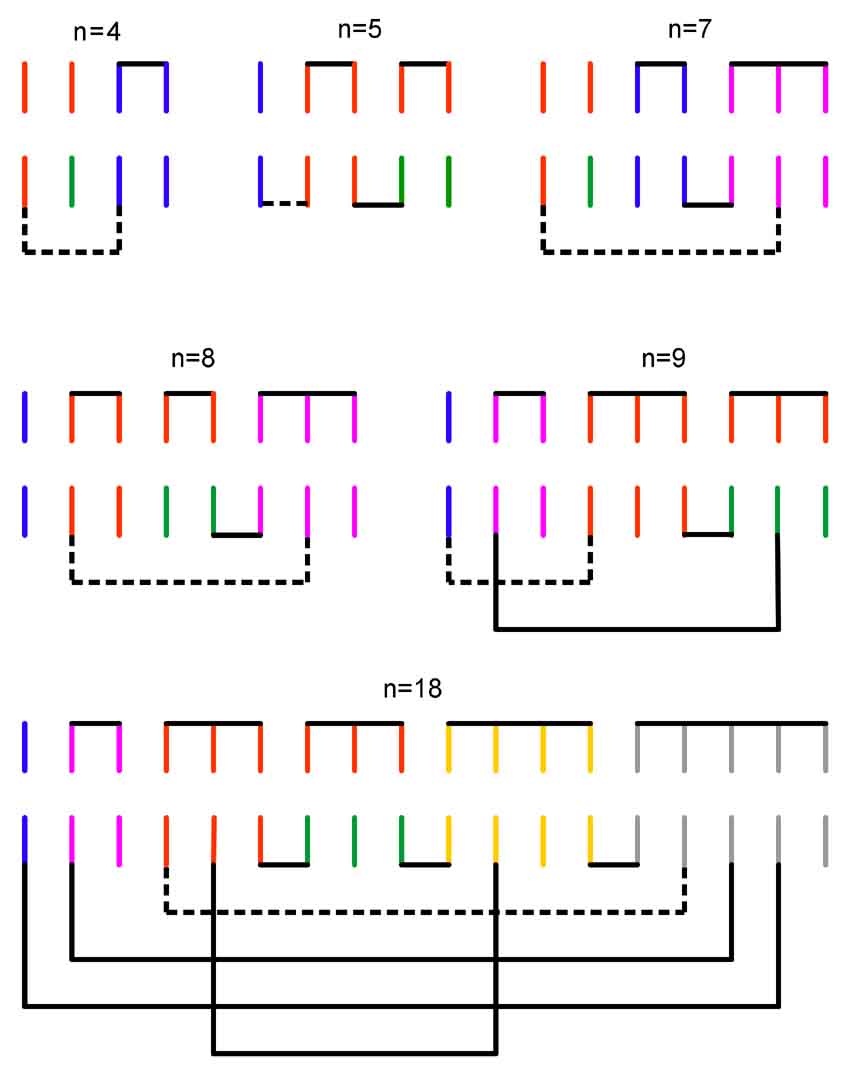
Aucun croisement de liens (en noir) ne correspond à un contact.
La partie du haut représente la première étape et celle du bas, la deuxième.
La troisième partie consiste à lire ce diagramme, en quelque sorte.

A noter que cette méthode reste valide pour [latex]k=0[/latex]. Il y a alors [latex]p[/latex] couleurs et autant de groupes discernables dès l'étape 2. Je donne pour exemple le cas de dix fils, il me semble qu'il s'agit d'une solution non-proposée. Elle me parait intéressante puisque je fais des économies de liens...


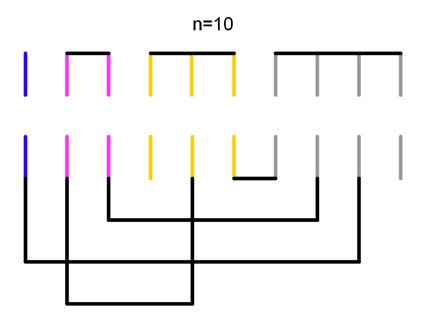
Ce fut bien laborieux, j'ai fait un nombre impressionnant de changements, mais je pense avoir trouvé une solution correcte (qui marche tout le temps).
J'y ai pris beaucoup de plaisir. Excellente énigme, merci.

Un petit message pour dire que je suis toujours là et pour applaudir les nouvelles interventions de Luthin et Dylasse qui proposent en fin de compte des solutions assez proches de celle de Scarta .

Je ne voudrais pas trop influencer les cerveaux en ébullition mais il y a une méthode radicalement différente et ( à mon sens ) plus jolie si on veut bien faire une croix sur les 1+2+3+...

Bon courage

Vasimolo

Bon je donne une autre solution bizarrement très simple

Il y a deux cas qui fonctionnent à peu près de la même façon , je détaille le cas où le nombre de fil est impair et je vous donne juste le schéma pour le cas pair .

Cas impair :



On branche les fils 2 par 2 , on laisse seul le fil rouge que l'on repère par un A .
On passe de l'autre côté et on repère facilement les paires de fil et le fil rouge . On ne peut bien sûr pas distinguer la paire 2-3 de la paire 4-5 mais ce n'est pas très important .
On branche le rouge A avec un deuxième fil disons jaune B puis le deuxième jaune C avec un violet D puis le deuxième violet E avec un premier marron F ...
On revient au point de départ et on défait les contacts mais en laissant les fils par paires .
Le fil en contact avec le A est B , le deuxième fil de la paire contenant B est C , le fil en contact avec C est D , ...

Cas pair :



Merci encore pour la participation et les belles illustrations ( je ne parle pas du dernier message )

Vasimolo