Bonjour!

Soit G un niveau de gris. On cherche les triplets (R,V,B) tels que R+V+B = 3G.
La valeur de B est ainsi fixée par celles de R et de V, il nous suffit donc de dénombrer les couples (R,V) tels que R+V <= 3G.
Choisir un tel couple revient à choisir R, puis à choisir R+V+1 dans [|0,3G+1|]. Il y en a donc 2 parmi 3G+2, ce que je note C(2,3G+2).
Conclusion: Pour un niveau de gris G, il y a C(2,3G+2) couleurs ayant ce gris.

Au temps pour moi! Il faut donc séparer les cas:
Si 3G <= 255, il y a bien C(2,3G+2) couleurs différentes de gris G.
Si 3G >= 2*255, on peut se ramener au cas précedent quitte à remplacer (R,V,B) par (255-R,255-V,255-B). Il y a alors C(2,3*255-3G+2)
Il reste à traiter les cas du milieu.
Supposons donc 3G dans [|256,2*255-1|]. Il y a C(2,3G+2) triplets (R,V,B) d'entiers tels que R+V+B=3G. On veut retirer ceux dont un élément est plus grand que 256. Remarquons que puisque 3G<2*255, il y a au plus un élément du triplet plus grand que 256. Nous allons donc dénombrer les triplets (R,V,B) tels que R+V+B=3G et R >= 256. En remplacant R par R-256, on est ramené au problème précédent. Nous disposons de C(2,3G-254) tels triplets. C'est la même chose si V>255 ou si B>255, on multiplie donc par 3.
Le nombre recherché est donc C(2,3G+2)-3*C(2,3G-254).
Je vérifie que la somme fait bien 256^3 et... c'est le cas

Coucou Sydre, un petit message pour te dire que j'ai presque fini mes équations. il y a un petit bug, mais je devrais bientôt en venir à bout.

== c) entre les deux N dans [255, 2x255] ==
ca se gâte. soit a tel que N=255+a
on va compter le plan complet moins les deux triangles A et B.



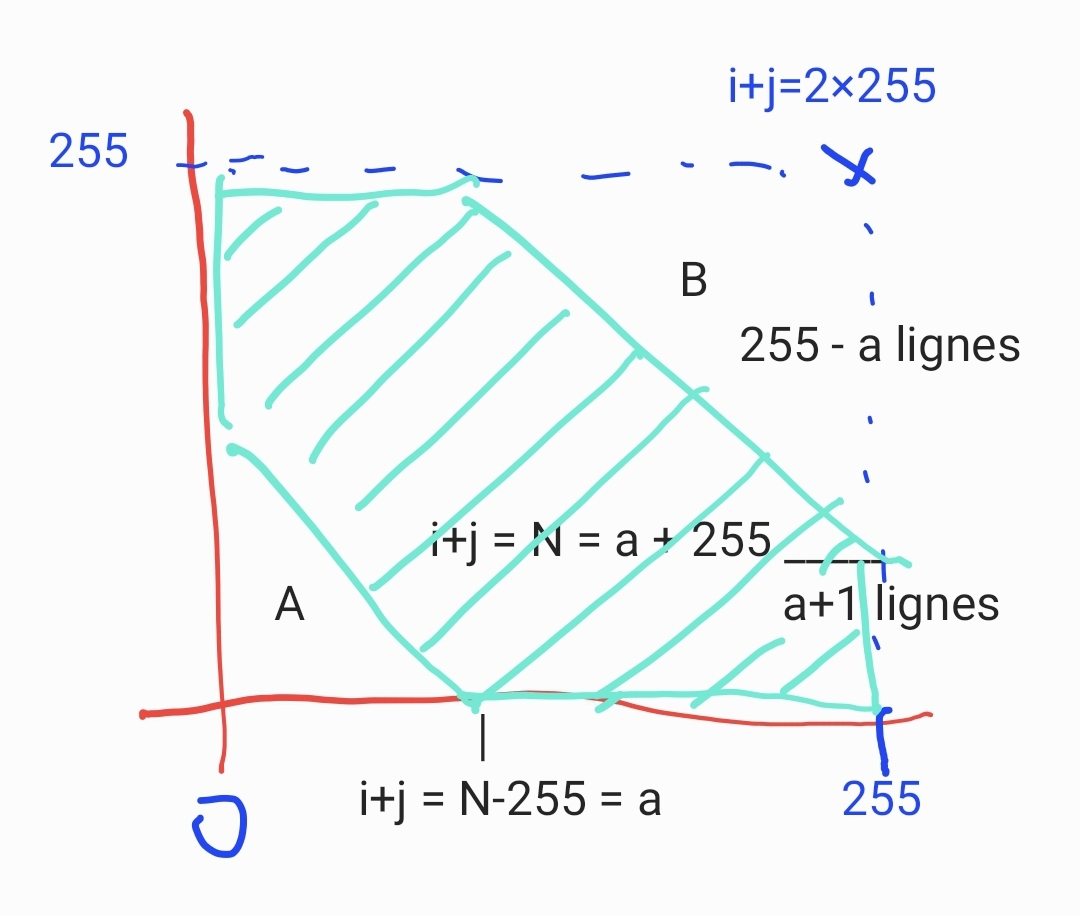
zone A : la plus grande ligne est composée de a valeurs (les colonnes de 0 à a-1)

d'où nb_A = 1 + 2 + ... + N-255 = (N-255)(N-255+1)/2

zone B : la plus grande colonne

somme des colonnes de 1 à 255-a
= 1 + 2 + ... + (2.255 - N) = (2.255-N)(2.255-N+1)/2

Reste à compter la zone centrale qui vaut f(N) = 256² - (N-255)(N-255+1)/2 - (2.255-N)(2.255-N+1)/2

je n'ai pas eu le temps de finir, mais ca fait une courbe parabolique en -N²

f(N) = -N² + 765N - 97154
 
je suis allé jeter un oeil au post de Sydre avec la courbe pointue. Ce qui est sûr c'est qu'on n'a pas la même chose. A creuser.

Petite vérification, mes trois tronçons de fonction f sont bien continus en 255 et en 2.255

f(255) = 32896 avec la formule  de la section (a) et celle de la section (c)

f(2×255) = 32896 également, autant avec la fonction (c) qu'avec la fonction (b)

Donc je suis plutôt bon sur ce point.

Bonjour à tous les trois

Je n'ai pas lu vos messages en détail mais j'ai aussi trouvé une fonction continue avec 3 branches de parabole et c'est complètement naturel car on tombe sur des sommes de [latex]C_k^2[/latex] . Une première chose est d'oublier la division par 3 dans la définition de G car elle nous sort inutilement du domaine des entiers . G évolue alors dans [[0;765]] . Je note N(k) le nombre de triplets de [[0;255]] de niveau de gris k/3 .

Dans la première zone : [latex]k \in [[0;255]] : N(k)=C_{k+2}^2[/latex] .

Dans la deuxième : [latex]k\in [[256;509]] : N(k)=2^{16}-C_{k-254}^2-C_{511-k}^2 [/latex] .

Dans la troisième [latex]k\in [[510;765]] : N(k)=C_{767-k}^2[/latex] .

Vasimolo

@Vasimolo C'est tout bon

@Spirou

Simple erreur de recopie lors du tracé. La courbe pointue correspond à [latex]C^2_{3G+2}-C^2_{3G-254}[/latex] (oubli du coefficient [latex]3[/latex])

Ce qui revient à ne pas eliminer tous les triplets avec un élément [latex]>255[/latex]