Enigme Lieu de points @ Prise2Tete

shadock · #1

Je reconnais ne pas avoir la réponse (ça fait 2 mois que je cherche ^^) mais je trouve le problème intéressant, avis aux amateurs :

Déterminer l'ensemble des points de coordonnées polaires : [latex](\frac{1}{cos(\theta)+sin(\theta)} , \theta)[/latex] avec [latex]\theta \in [0; \frac{\pi}{2}][/latex]

Amusez vous bien.

NB : Je précise qu'à la fin de ce chapitre, je ne connaissais que les formules suivantes
[TeX]r=sqrt{x^2+y^2}[/TeX]
[TeX]x=r.cos(\theta)[/TeX]
[TeX]y=r.sin(\theta)[/TeX]
Shadock

L00ping007 · #2

C'est en fait tout simple !

Les coordonnées cartésiennes des points de cette courbe sont les suivantes :
[TeX]x(\theta)=r(\theta)cos(\theta)
y(\theta)=r(\theta)sin(\theta)[/TeX]
où [latex]r(\theta)=\frac1{cos(\theta)+sin(\theta)}[/latex]

Si on somme [latex]x(\theta)[/latex] et [latex]y(\theta)[/latex], on trouve ...
[TeX]x(\theta)+y(\theta)=1[/TeX]
La "courbe" est donc incluse dans la droite d'équation [latex]y=1-x[/latex]

En remarquant que pour [latex]\theta[/latex] dans [latex][0;\frac{\pi}2][/latex] :
[TeX]r(\theta) \ge 0
cos(\theta) \ge 0
sin(\theta) \ge 0[/TeX]
alors x et y sont positifs.

Finalement, ta courbe paramétrée décrit le segment joignant les points (1,0) et (0,1)

mitsuidewi · #3

Il semble qu'il y a une infinité de points.

Tout simplement parce qu'il n'y a pas vraiment de conditions, simplement des points à placer avec thêta de 0 à Pi/2 (et il y a une infinité de points entre 0 et Pi/2)

Les points représentent le segment en gras.

franck9525 · #4

Déterminer l'ensemble des points de coordonnées polaires. C'est quoi ce type de question ?? quelle sorte de réponse peut-on bien donner ? Descriptive : un morceau d’ellipsoïde ou la lettre C ? Numérique : voir question ? un ensemble de valeurs ?

SHTF47 · #5

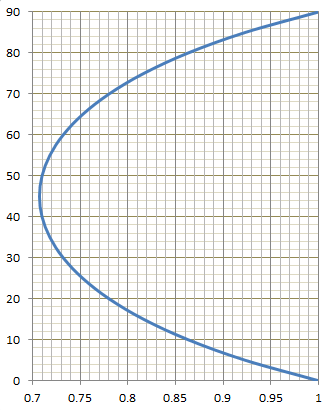
Un petit graphe sur Maple montre que l'ensemble cherché est le segment d'extremités [1,0] et [0,1]

Tromaril · #6

Bonjour,

Tu utilises les formules de calcul de x et y
tu les sommes
et ça te donnera la réponse

halloduda · #7

Ne serait-ce pas tout simplement le segment de droite qui relie les points (0, 1) et (1, 0) ?
En remarquant que :[latex]\rho.\cos\theta+\rho.\sin\theta=x+y=1[/latex] avec [latex]0\leq\theta\leq\frac\pi2[/latex].

Plus rigolo serait cet autre problème :
[TeX]\rho=\sin\theta+\cos\theta[/TeX]
La solution par inversion de pôle O : l'arc de cercle (0, 1), (1, 1), (1, 0)

Yanyan · #8

Soit la similitude directe [latex]f(z)=(1-i)z-1+i[/latex].

Les points considérés sont d'affixes [latex]\frac{cos \theta + isin \theta}{cos \theta+ sin \theta}[/latex]

La similitude les transforme en [latex]sin(2 \theta) i[/latex]

C'est-à-dire en le segment d'extrémités 0 et i, l'ensemble de points cherchés est aussi un segment: l'image de [0,i] par la transformation inverse [latex]g(z)=\frac{1+i}{2}z-1[/latex]

L'idée me semble bonne mais les calculs sont peut-être faux.

Les calculs sont bien faux (une erreur dans un signe,désolé) et la réponse des autres est plus simple, bravo!

shadock · #9

Merci à tous, je pense avoir compris

mitsuidewi · #10

On devrait établir les votes pour la meilleur explication, en l'occurrence je vote pour Looping qui a été très pédagogique. Par contre avec un dessin ca aurait été encore mieux !

L00ping007 · #11

Merci, mais c'est vrai que je suis pas toujours doué pour les dessins au propre, et mes brouillons sont pas beaux D'autres le font parfaitement, travail d'équipe :-)

shadock · #12

Même si la version de L00ping007 est très bien je ne comprends pas la somme de [latex]x(\theta)+y(\theta)[/latex] Je ne sais pas si c'est grave mais c'est le cas.

L00ping007 · #13

[TeX]x(\theta)=r(\theta)cos(\theta)<br />y(\theta)=r(\theta)sin(\theta)[/TeX][TeX]r(\theta)=\frac1{cos(\theta)+sin(\theta)}[/TeX]
Tout est là, pourtant, il suffit d'additionner et de simplifier

shadock · #14

Bah j'ai bien essayé mais je n'y arrive pas.
[TeX]x(\theta)+y(\theta)=r(\theta)\left(cos(\theta)+sin(\theta)\right) [/TeX]
Comme [latex]r(\theta)=\frac{1}{cos(\theta)+sin(\theta)}[/latex] alors [latex]x(\theta)+y(\theta)=1[/latex] a oui c'est bon c'est tellement tard.

Excuse pour le dérangement et merci

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 19-03-2011 00:53:41

Lieu ed points

#0 Pub

#2 - 19-03-2011 01:36:23

iLeu de points

#3 - 19-03-2011 02:24:42

Lieu d points

#4 - 19-03-2011 09:21:48

Lieu de pooints

#5 - 19-03-2011 10:33:57

lieu de pointq

#6 - 19-03-2011 10:48:46

Lieu de ponts

#7 - 19-03-2011 12:47:13

lieu de poinys

#8 - 21-03-2011 19:54:31

Lieu de poitns

#9 - 22-03-2011 21:03:06

Lieu e points

#10 - 22-03-2011 22:46:01

lieu fe points

#11 - 22-03-2011 23:36:27

Lieu de poinnts

#12 - 29-07-2011 03:59:01

lieu de ppints

#13 - 29-07-2011 04:33:35

Lieu d epoints

#14 - 29-07-2011 04:54:04

lieu de ppints

Réponse rapide

Sujets similaires

Mots clés des moteurs de recherche

Pied de page des forums