Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 30-08-2011 22:23:48
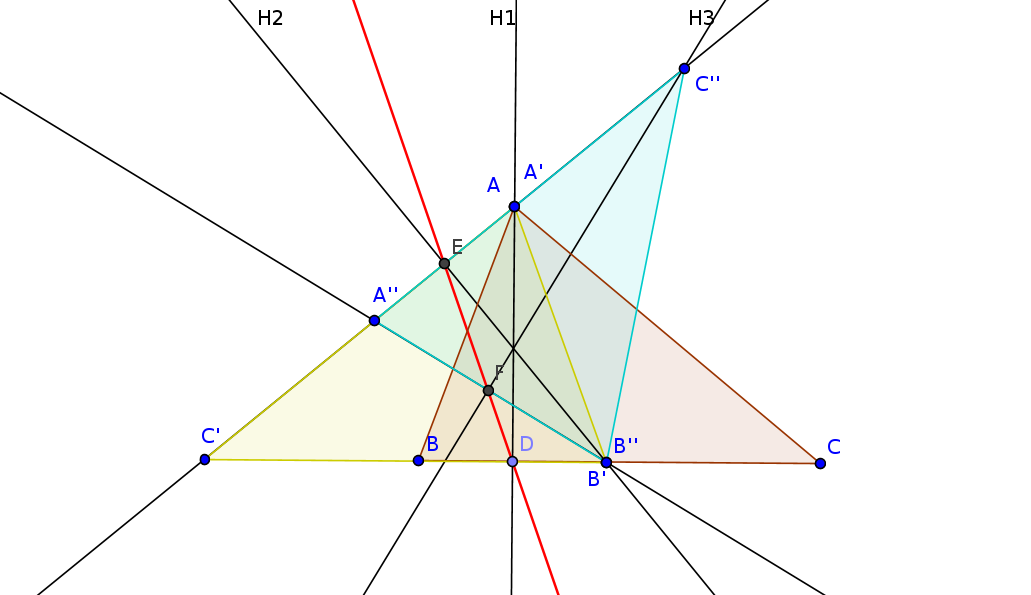
Symétries et alignement de ponitsVoici un problème de géométrie un peu plus compliqué que les énigmes que j'ai proposé précédemment.
#0 Pub#2 - 31-08-2011 00:24:27
syméteies et alignement de pointsBonsoir, #3 - 31-08-2011 08:16:24
symétries rt alignement de points@esereth : #4 - 31-08-2011 14:59:14
Symétries et alignement de pointssBonjour, #5 - 31-08-2011 15:14:59
dymétries et alignement de pointsBonjour, #6 - 31-08-2011 16:45:21
symétries et alignement de poinys@esereth : Pour joindre une figure, tu cliques sur Upload au dessus de ton cadre où tu tapes ta réponse. Ensuite tu cliques sur Parcourir, tu sélectionnes ton image et tu complètes le dernier cadre avec le code inscrit sur le pictogramme. Tu appuies sur "Uploader ce fichier". La page suivante te donne l'adresse vers l'image, tu n'as qu'à la copier coller sur ta réponse Réponse rapideSujets similaires
Mots clés des moteurs de recherche |
 | |||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.