En fait, pour t'aider, fait le dessin sur une feuille a plat et dessine le maximum de liaisons possibles... quelque soit ton dessin ca sera equivalent, il en manquera une...
Hé bien si tu pouvais faire le tour du monde, en faisant le tour du cylindre (ou de la sphere, ca revient au meme), ca ne t'aiderait en rien a resoudre le probleme, parce que la croix et le carré restant à relier sont séparés par une boucle fermée constituée des autres liaisons, qui entoure et isole soit un carré soit une croix (la boucle, c'est la fameuse courbe de jourdan qui coupe l'espace en deux parties distinctes, contenant une la croix et l'autre le carré...)
La démonstration que c'est impossible passe par là : en voilà une ébauche simpliste qui devrait te convaincre.
j'appelle x1 x2 et x3 les croix à relier à o1 o2 et o3 chacune... Si je peux tout relier je peux faire le tour de ces liaisons selon la boucle
x1 -> o1 -> x2 -> o2 -> x3 -> o3 -> x1 (j'utilise 6 liaisons sur 9)
Cette boucle est fermée sur elle-même et je ne peux plus la couper...
Donc les autres liaisons sont soit dedans, soit dehors, et il en reste 3.
Or que ce soit dedans ou dehors, on ne peut y dessiner qu'une seule liaison : ce dessin devrait suffire à le comprendre pour le dedans (en patés rouges les croix et patés verts les carrés, on a jamais vraiment eu besoin des numéros...) :
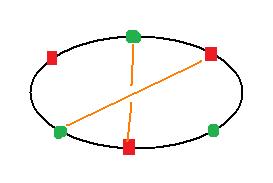
et pour le dehors c'est pareil (par exemple sur la sphere, dedans et dehors n'ont pas vraiment de sens... les deux sont pareil, et donc si c'est pas possible sur la sphere, c'est pas possible sur le ruban ou le papier plat)... On a donc 8 liaisons possibles, mais la neuvième ne l'est pas, d'ou l'impossibilité de résoudre cette énigme.
Et quand on a fait 8 liaisons, on a quelquechose d'équivalent à l'image dessous, ou les 8 liaisons sont en noir. Le bleu qui dédouble les liaisons est la fameuse courbe de Jourdan qui sépare distinctement les deux derniers points à lier, et qui sert mathématiquement à dire que c'est impossible :
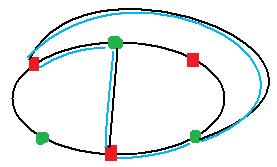
Enfin, pour revenir a la relation entre dessin plat, sur cylindre ou sur la sphere, il suffit de te dire que tu peux représenter la sphere et le cylindre à plat (la sphere sauf un point pour etre precis; mais le cylindre en entier, qui donnerait comme CD avec un trou au milieu)... vu comme ca, cela montre que c'est en fait encore plus dur sur le cylindre qu'à plat (parce que le cylindre est comme une feuille de papier privée d'un trou au milieu; et ce que tu pouvais concevoir comme un gain de liberté et de possibilités de faire le tour du cylindre revient a faire des tours en rond à plat autour d'un trou en réalité, ce qui sert pas à grand chose).
Fiou, j'espère avoir été clair,
cheers

 Accueil
Accueil
 Forum
Forum








