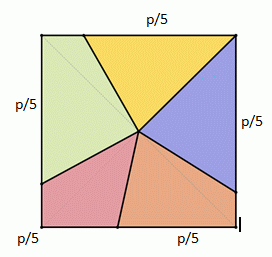
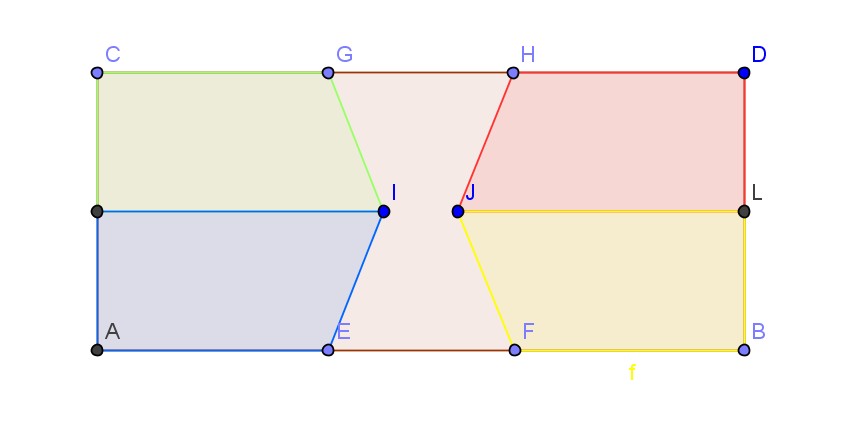
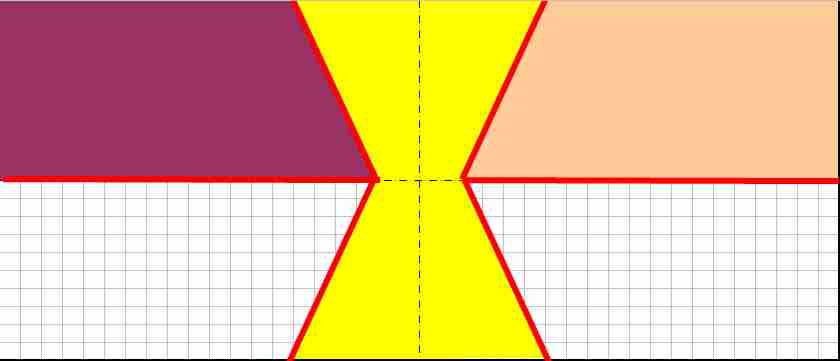
Je pense à un découpage comme ci-dessous, dessin fait à la va-vite :
Les obliques situées sur la longueur sont centrées en 0,4*L et 0,6*L. Il me reste à trouver la bonne inclinaison...
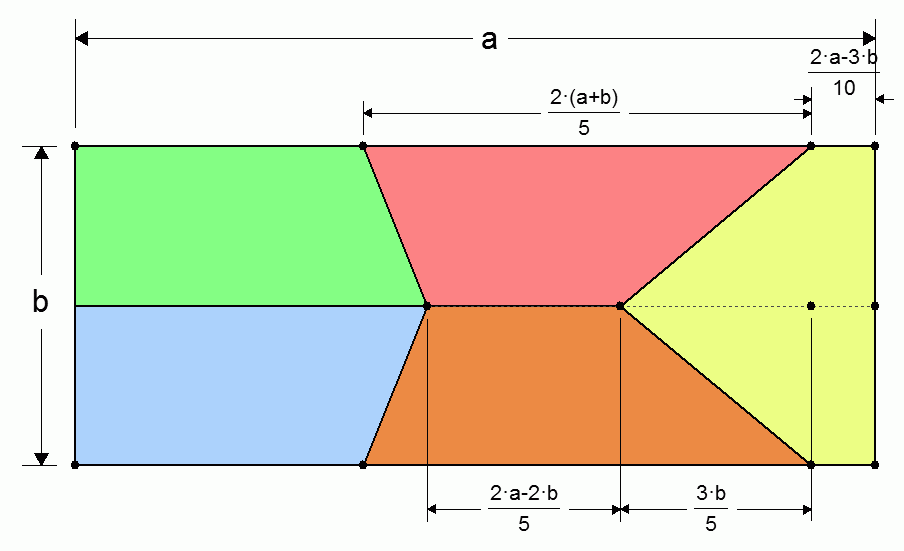
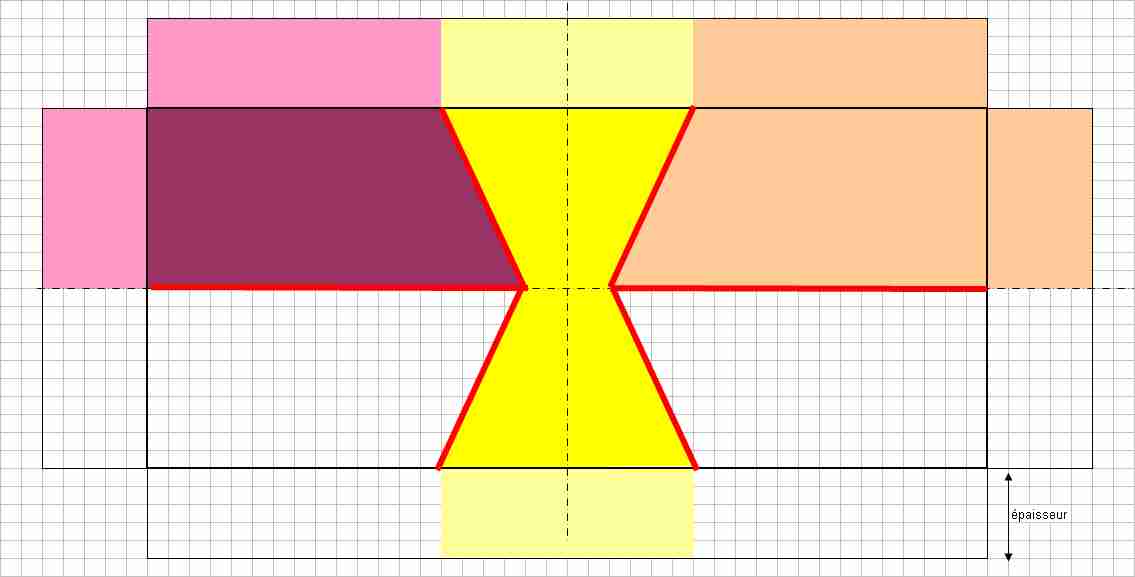
La surface latérale brune compense celles des autres parts qui lui sont parallèles.
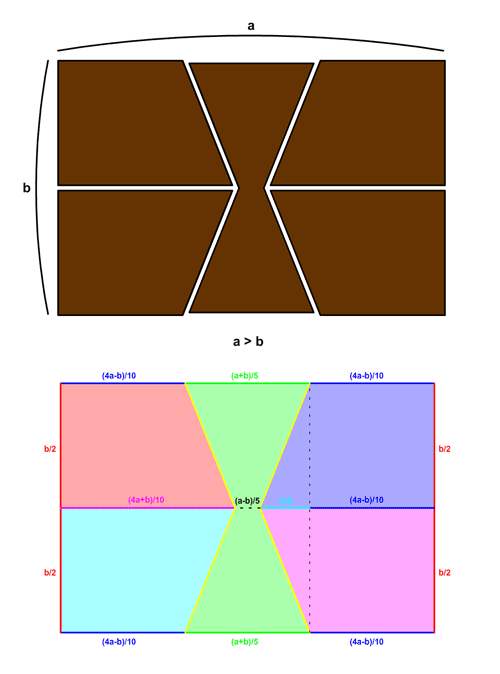
Il reste à placer les coups de couteau supérieurs, entre kL et (1-k)L par symétrie pour le brun. Je dois avoir (1-2k)L*l=kL*0,5l+h*0,5l donc 2-4k=k+(h/L).
On en tire k=0,2*(2-(h/L))
Cette méthode ne convient que si k est supérieur ou égal à 0,3 sinon les deux coupes obliques se rejoignent avant la fin...
La méthode décrite ci-dessus ne vaut que si la hauteur n'excède pas la moitié de la longueur. Mais elle se fait en quatre coups de couteau 
Deuxième cas : h>0,5L
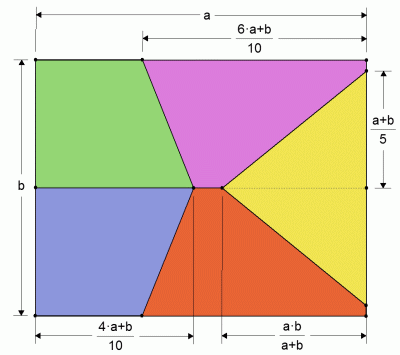
Je propose également, par deux coups de couteau obliques, de faire une part en forme de prisme, puis de partager le reste en deux coups de couteau selon les médianes du rectangle de base. Les calculs restent à faire pour la hauteur du prisme et ses limites sur la face supérieure...
Mes calculs donnent pour le prisme une hauteur d valant [latex]d=\frac{2hL}{L+2h}[/latex] et la même formule pour k que dans le premier cas : [latex]k=\frac{2L-h}{5L}[/latex]
_______________________________________________________
Horreur ! Je viens de voir que ça ne marche plus si h>2L...
Troisième cas : h>2L
Je décrète qu'il est interdit de faire un gâteau dont la hauteur dépasse le double de la longueur. Non mais !...
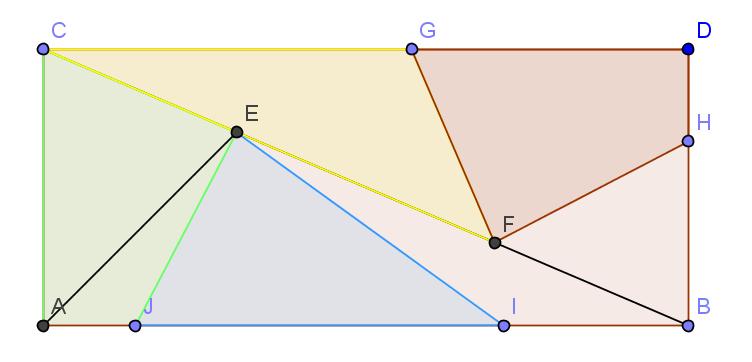
On place le couteau à une distance (h-2L)/5 du haut. On découpe sur la face avant un pentagone dont l'aire vaut 1/5 du total de cette face.
That's all, folks!
Accueil
)
non je sais personne n'a de laser assez puissant chez lui pour faire ce genre de chose! 
