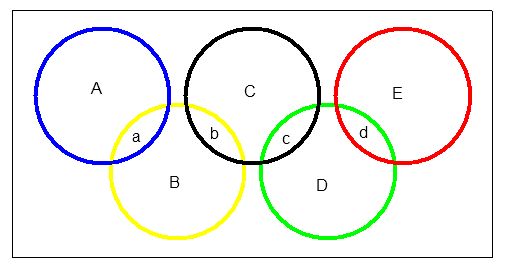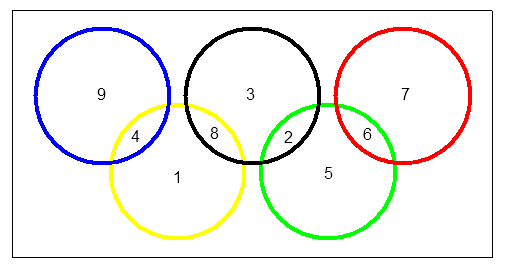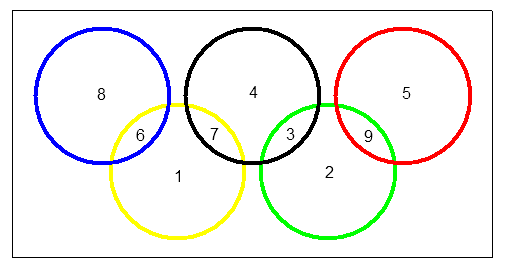|
#1 - 06-08-2016 00:19:13
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gââteau 125
Pour l'ouverture des jeux olympique mon pâtissier a reçu une curieuse commande :
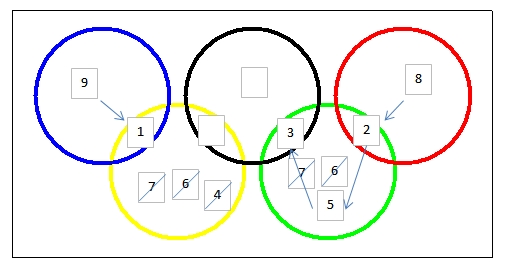
Il doit disposer 45 médailles dorées dans les 9 zones délimités par les 5 cercles . Chacune des zones doit contenir au moins une médaille et deux zones ne doivent jamais contenir le même nombre de médailles . Il faudrait en plus que chaque disque ait le même nombre de médailles et que celui-ci soit le plus grand possible .
Comment va-t-il s'y prendre ???
Amusez-vous bien
Vasimolo
#2 - 06-08-2016 07:18:14
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,002E+3
GGâteau 125
Pour les deux extrêmes, pas possible de faire 2 sommes à 17, ni à 16.
On peut faire 2 sommes à 15 (9-6 et 7-8) mais le cercle central donnera 12 au maximum.
Reste à tenter 14 :
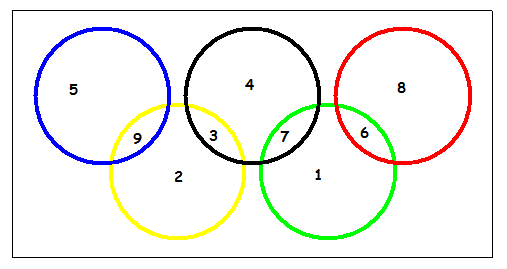
#3 - 06-08-2016 09:37:08
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
gâyeau 125
Toujours aussi rapide Gwen 
Ceux qui ont fini peuvent essayer de montrer qu'à une symétrie près la solution est unique .
Vasimolo
#4 - 06-08-2016 10:52:43
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Gâtaeu 125
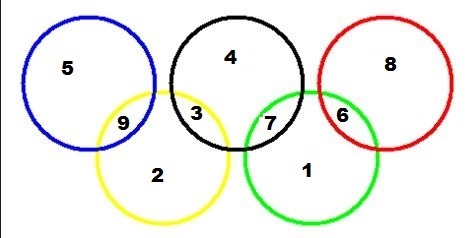
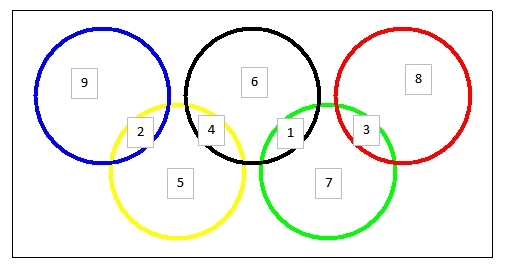
Pour trouver le nombre maximal de médailles par disque, j'ai considéré qu'il faudra remplir les 3 disques (bleu, noir, rouge) qui n'ont pas de zone commune et voir le max qu'ils peuvent recevoir. Comme chaque zone doit avoir au moins 1 médaille, j'ai rempli les zones "propres" aux disques vert et jaune avec 1 et 2 médailles. Il reste 42 médailles, ce nombre divisé sur les 3 disques "distincts": 42/3=14. Il ne reste plus qu'à bien les placer!
Le disque bleu doit avoir 14 médailles sur 2 zones: 9 et 5 sont les seuls chiffres disponibles qui peuvent satisfaire cela.
Le disque rouge doit avoir 14 médailles sur 2 zones: 9+5 ou 8+6 or 9+5 est déja utilisé donc il ne reste que le 8+6.
Le disque jaune a déja 2 et 9, il faut 3 pour dans la zone noir/jaune
Le disque vert a déja 1 et 6, il faut 7 pour dans la zone noir/vert
On vient de remplir le disque noir de 3 et 7, il reste 4 pour atteindre 14.
Si au début, j'avais placé 1 médaille dans le disque jaune et 2 dans le disque vert, le placement sera simplement symétrique au placement actuel.
#5 - 06-08-2016 12:07:10
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Gâteau 152
J'ai trouvé 4 solutions à la main (liste pas forcément exhaustive) :
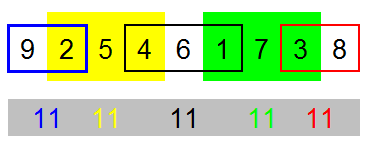
9 2 5 4 6 1 7 3 8 somme 11
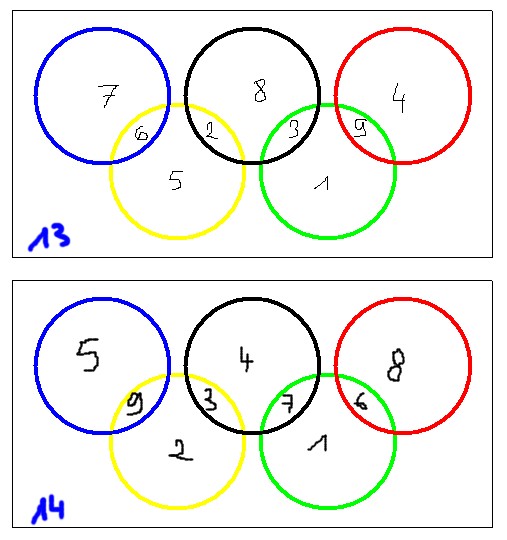
7 6 5 2 8 3 1 9 4 somme 13
7 6 5 2 3 8 1 4 9 somme 13
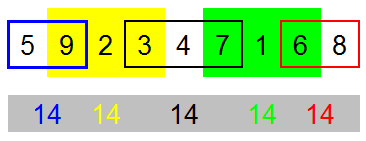
5 9 2 3 4 7 1 6 8 somme 14
En partant du fait que la somme des 4 intersections est un multiple de 5.
#6 - 06-08-2016 12:22:43
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 1255
Bien vu Kossi 
@Nodgim : chaque continent ( ie : disque ) doit récupérer un maximum de médailles .
Vasimolo
#7 - 06-08-2016 12:56:32
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
gâteay 125
Bien sûr, il ne reste donc que la dernière solution:
5 9 2 3 4 7 1 6 8 somme 14.
Comme je le disais, la somme des intersections doit être un multiple de 5, car la somme de 1 à 9 fait 45, à laquelle on ajoute 2 fois la somme des intersections.
Les combis des intersections pour une somme 14 sont :
1 7 8 9
2 6 8 9
3 5 8 9
3 6 7 9
4 5 7 9
4 6 7 8
(A noter que la seule combi des intersections ayant pour somme 15 est 6 7 8 9, et qu'on ne peut en tirer de solution)
On joue alors, entre autre, sur le fait que les valeurs < 5 ne concernent pas les disques d'extrémités. Seule la combi 3 6 7 9 convient.
#8 - 06-08-2016 14:01:03
- Agid1915
- Passionné de Prise2Tete
- Enigmes résolues : 0
- Messages : 50
#9 - 06-08-2016 14:08:37
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1821
Gâetau 125
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#10 - 06-08-2016 14:47:28
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
#11 - 06-08-2016 15:45:04
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
gâteay 125
@Nodgim et Enigmatus : oui 
@NickoGecko : Tu dois pouvoir distribuer un peu plus de médailles à chaque continent .
Vasimolo
#12 - 06-08-2016 18:18:03
- bidipe
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1126
- Lieu: Côte basco-landaise
Gâtea u125
Bonjour
les 9 zones devant contenir des nombres différents dont la somme est 45, les zones sont donc occupées par les chiffres 1,2,3,4,5,6,7,8,9 dont la somme est bien 45
b+c+d=f+g+h donc b+c+d+f+g+h = pair donc a+e+i = impair
c,d,e,f,g !=9
Si b+c+d+f+g+h =22 alors b+c+d=f+g+h = 11 = 2+4+5=1+3+7
Bref, ce n'est pas vraiment une démonstration 
mais je trouve ca 
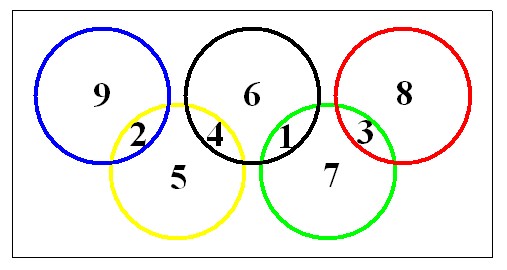
Edit : argh, je crois que j'ai une meilleure solution, je reviens 
Ah ben non, je ne trouve pas, et le soleil m'attend 
#13 - 06-08-2016 19:06:43
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâeau 125
@Bidipe , profites bien du soleil 
S'il te reste un peu d'énergie reprends tes calculs . Je me verrais bien faire ça sur la plage avec des galets ou des coquillages , mais bon ...
Vasimolo
#14 - 06-08-2016 19:21:09
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,002E+3
Gâtea u125
Justifier l'unicité...
14 dans tous les ronds, c'est 4 3 7 au milieu, et donc, 1 et 2 en bas.
Le 1 est avec 9 5 ou 8 7 ... Dans une des hypothèses, le 4 doit être des deux côtés à la fois, impossible. Dans l'autre, il n'y a pas le choix, on aboutit à la solution.
#15 - 06-08-2016 19:38:58
- bidipe
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1126
- Lieu: Côte basco-landaise
#16 - 06-08-2016 19:58:01
- elpafio
- Elite de Prise2Tete
- Enigmes résolues : 43
- Messages : 1017
#17 - 06-08-2016 21:05:08
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
gâteai 125
Bravo à tous sauf à Elpafio .
Vasimolo
#18 - 07-08-2016 18:29:25
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Gâteua 125
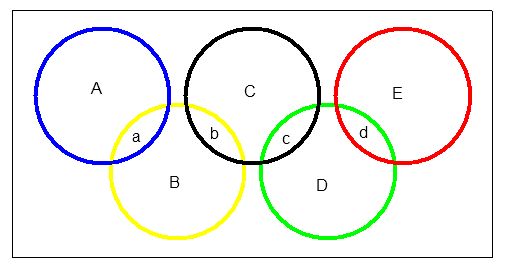
A = 9+(-4a+b+c+d)/5 => b+c+d =< 4a
B = 9+(-4a-4b+c+d)/5 => c+d =< 4a+4b
C = 9+(a-4b-4c+d)/5 => a+d =< 4b+4c
D = 9+(a+b-4c-4d)/5 => a+b =< 4c+4d
E = 9+(a+b+c-4d)/5 => a+b+c =< 4d
On voit que: a+b+c+d doit être multiple de 5.
On voit aussi que a et d ne peuvent pas valoir 1.
Après quelques tests, on trouve deux solutions:
A=9 / a=2 / B=5 / b=4 / C=6 / c=1 / D=7 / d=3 / E=8
A=9 / a=4 / B=1 / b=8 / C=3 / c=2 / D=5 / d=6 / E=7
la seconde maximisant chaque disque.
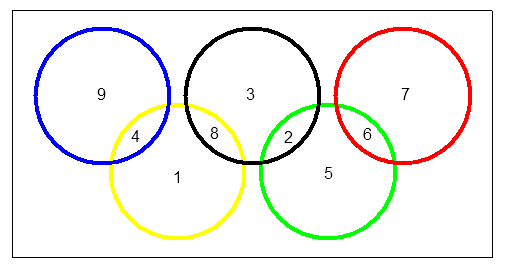
#19 - 07-08-2016 18:59:44
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 25
Tu dois pouvoir être un peu plus généreux Franky 
Vasimolo
#20 - 07-08-2016 21:19:45
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
gâtezu 125
Avec des disques de 15, je ne trouve rien, mais avec 14, c'est surement celui-ci (ou son symétrique).
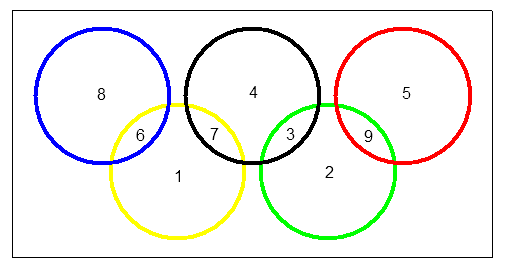
#21 - 07-08-2016 22:39:59
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
gâtzau 125
Et pourquoi pas plus ?
Vasimolo
#22 - 08-08-2016 08:47:59
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
gâtzau 125
Si on veut plus, c'est-à-dire des disques de 15, alors on doit à la fois placer 6, 7, 8 et 9 sur les zones centrales et placer 2 de ces nombres sur les disques extrêmes pour faire une somme de 15, ce qui est impossible. Des disques de 14 constituent donc un maximum. Merci pour ce divertissement olympique.
#23 - 08-08-2016 18:37:13
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâtau 125
Bravo et merci 
Vasimolo
#24 - 09-08-2016 19:08:05
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâetau 125
Merci à tous ceux qui se sont amusés à cette petite récréation olympique : l’essentiel est de participer 
Vasimolo
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum