shadock : juste pour savoir c'est quoi ton record?
Personnelement si le but est d'arriver à 25 carrés au total je dis que c'est impossible et qu'il faudrait rajouter au moins 1 ou 2 carré supplémentaire pour y arriver. smile

Je ne pense pas avoir dépassé 16 carrés.

C'est vrai que quelques règles de base de topologie interdisent d'aller loin (les noeuds sur les bords étant connectés au réseau par un nombre impair de segments possibles, seuls deux d'entre eux (l'origine et la fin du trajet) peuvent être totalement connectés à leur voisins.

J'ai l'intuition que ça pourrait limiter le maximum possible à 17 carrés.

le truc : a ton le droit de sortir du " grand carre "
par la je veut dire peut on deborder et revenir en suite ( voir la resolution de l'enigme ou il faut relier 9 point

.    .    .
.    .    .
.    .    .

à dhrm77 : Le périmètre de la grille est déjà tracé au départ. Il ne peux donc pas y exister une ouverture comme sur ton dessin.

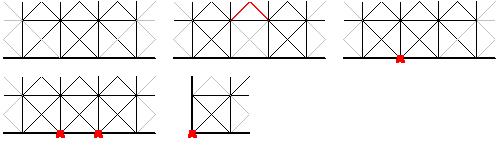
Sans lever le crayon et en revenant à son point de départ, on peut déjà faire un truc dans ce genre

,---,---,---,---,---,
|   | X |   | X |   |
|---|---|---|---|---|
| X |   | X |   | X |
|---|---|---|---|---|
|   | X |   | X |   |
|---|---|---|---|---|
| X |   | X |   | X |
|---|---|---|---|---|
|   | X |   | X |   |
'---'---'---'---'---'

On a 12 carrés, on va appeler ça la "grille de base".

Après, il faut voir qu'est-ce qu'on pourrait ajouter à ça en suivant ces règles:
- On ne peut ajouter qu'un seul chemin.
- On le commence et on le finit où l'on veut.
- On ne peut pas repasser sur des traits de la grille de base qui sont sur le périmètre de la grille (déjà tracés à la base)
- On peut repasser sur des traits de la grille de base, à condition d'utiliser, pour chaque sommet, un nombre pair de traits présents sur la grille de base (autrement dit, pour un sommet donné, on peut utiliser deux traits de la grille de base pour ce sommet, voire 4 ou même aucun, mais pas 1 ou 3)
- On peut tracer des traits qui n'existent pas sans condition
- On ne peut pas repasser sur des traits de ce chemin

Ensuite, on enlève de la grille de base les traits qu'on utilise sur notre chemin: a priori, ça reste un graphe dans lequel on peut trouver un cycle eulérien. Et pour finir, on trace notre chemin de bout en bout, avec un petit "détour" à un moment, pour tracer notre cycle eulérien, revenir au point de départ du "détour" et finir le chemin.

Ca c'est pour la théorie. En pratique, j'ai pas de papier crayon sous la main, mais de tête, j'arrive pas à trouver de tels chemins qui pourraient augmenter notre résultat de 12...

Bonjour,

je ne vois pas comment on pourrait faire 17 carrés pleins :
- Soit on a 8 carrés pleins au bord et le carré 3x3 central est plein mais il y a trop de sommets d'où un nombre impair de segments partent...
- Soit on a 9 carrés pleins au bord mais trois des quatre carrés aux coins du carré central devront être plein et il y aura encore trop de sommets d'où un nombre impair de segments partent.
Si il y a plus de carrés au bord, il y a trop de sommets "impairs".

Pour avoir 16 carrés pleins, il en faut au moins sept au bord car seuls neuf carrés ne touchent pas un bord. Voici toutes les configurations possibles sur les bords ou sur les coins :

On remarque que quelque soit la configuration utilisé sur un bord, le nombre de sommets "impairs" (d'où un nombre impair de segments partent) est toujours supérieur ou égal au nombre de carrés pleins plus un. Le deuxième cas est une exception car il ne contient pas de sommet "impair" mais ce n'est vrai que si les trois carrés au-dessus ne sont pas tous les trois pleins et donc il faut ajouter un carré plein de plus sur le bord. Il est donc équivalent au premier cas.
Un coin plein crée un sommet "impair" de plus.
Donc dans tous les cas, pour chaque carré plein sur un bord exceptés les quatre premiers (un pour chaque côté), on a au moins un sommet "impair" de plus.
Or, la théorie des graphes nous interdit d'avoir plus de deux sommets "impairs", on peut donc avoir au maximum six carrés pleins sur les bords ce qui ne suffit pas pour avoir 16 carrés pleins en tout.