|
#1 - 20-06-2011 10:04:14
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
construvtion avec 12 murs perpendiculaires
Salut à tous!
Cette semaine une énigme qui va bien se prêter à un classement que je tenterais de mettre à jour régulièrement!
Vous avez 12 murs, d'épaisseur négligeable, de longueur 1 à 12.
Vous devez tous les utiliser pour former un polygone.
D'un mur au suivant il doit y avoir systématiquement un angle droit.
(Ce qui interdit donc de mettre 2 murs bout à bout sans changer de direction)
(Si vous avez bien compris vous devez voir qu'il n'y a que deux directions possibles).
Il est interdit de croiser le polygone.
Il est interdit de superposer 2 murs même partiellement.
Il est interdit de superposer 2 coins.(vous finirez par comprendre cette phrase.)
1)Quelle est l'aire maximale que l'on peut obtenir?
2)Quelle est l'aire minimale que l'on peut obtenir?
C'est parti!
Je ferais 2 classements séparés mis à jour au moins 1 fois par jour. 
CLASSEMENT:
(Maintenant que j'affiche les valeurs de chacun je ne le mettrais plus à jour)
Aire maximale:
1 ex-aequo) golgot59, w9Lyl6n, gwen27, SHTF47 319
5 ex-aequo) NickoGecko, nodgim, dylasse 317
8) looozer 314
9) Bamby2 307
10) socato314 305
11) franck9525 293
Aire minimale:
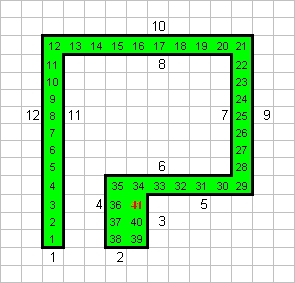
1 ex-aequo) golgot59, NickoGecko, w9Lyl6n, SHTF47, gwen27, looozer, Bamby2, nodgim 41
9) dylasse
10) franck9525 58
Je ne donne volontairement pas les valeurs obtenues par chacun pour le moment.
#2 - 21-06-2011 09:12:39
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1821
Construction aec 12 murs perpendiculaires
Bonjour
J'ai une première proposition pour l'aire minimale à 42 :
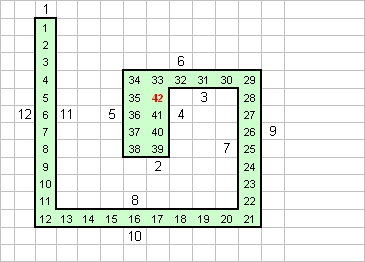
A améliorer !
Je cherche + l'aire maximale !
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#3 - 21-06-2011 09:24:05
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
construction abec 12 murs perpendiculaires
Te voila donc premier du classement pour l'aire minimale :p
#4 - 21-06-2011 09:45:28
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Construciton avec 12 murs perpendiculaires
Bonjour,
J'obtiens 319 pour l'aire maxi et 41 pour l'aire mini... J'ai bon ? 
#5 - 21-06-2011 10:00:40
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Construction avec 12 murs perpeendiculaires
Tu es donc ajouté au classement, pour le moment je ne donne pas d'indication, suffit de regarder si quelqu'un arrive à te battre 
#6 - 21-06-2011 10:43:17
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1821
Coonstruction avec 12 murs perpendiculaires
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#7 - 21-06-2011 13:14:18
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Construction avec 12 murs perpendiculairres
Pour info, pour l'aire mini, je place 12, puis 10 en tournant à droite, puis 9 à droite, puis 5 à D, 3G, 2D, 4D, 6D, 7G, 8G, 11G, 1D.
Pour l'aire maxi 12, 3D, 7G, 11D, 4D, 5G, 10D, 2D, 6G, 9D, 1D, 8G.
#8 - 21-06-2011 14:52:03
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Construction avec 12 murs perpendiculares
@NickoGecko: il y a une erreur si tu regardes ton segment de 12 dans l'aire mini. Je me suis permis de corriger donc le calcul car c'est trivial.
@golgot59: Calcul vérifiés et validés classement mis à jour.
#9 - 21-06-2011 15:48:27
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
construction avec 12 murq perpendiculaires
Bonjour à tous,
alors voilà c'est mon premier message sur ce forum, que je suis depuis quelques mois mais comme je suis flemmard je n'ai jamais donné mes solutions aux énigmes jusqu'à maintenant.
Tout d'abord la somme des longueur des cotés vaux 1+2+...+12 = 12*13/2 = 78 , donc d'après le théorème de Pick (déjà vu ici: http://www.prise2tete.fr/forum/viewtopic.php?id=5425) l'aire des polygones est minorée par 0+78/2-1 = 38 (cas où il n'y aurait aucun point à l'intérieur) et très grossièrement est majoré par (78/4)² donc par 380.
Bon tout ça on s'en fou un peu. Plus intéressent, puisque les cotés "verticaux" alternent avec les cotés "horizontaux" il y a exactement 6 cotés horizontaux et 6 verticaux. De plus si on tient compte du sens de parcours la somme des longueurs "signées" est nulle dans chaque direction (on revient au point de départ du polygone).
Une fois qu'on a partagé les entier de 1 à 12 en deux groupe de 6 et qu'on a trouvé une manière de les signer pour obtenir une somme nulle, il reste environ 5! * 6! = 86400 combinaisons à tester (en fixant le premier coté)
Comme je l'ai dis, je suis flemmard, mais aussi un peu perfectionniste, j'ai donc essayé d'expliquer mon problème au grand Ordix dans le langage caml (langage inintelligible pour le commun des mortelles et pour les autres aussi, bref parfait pour une prise de tête).
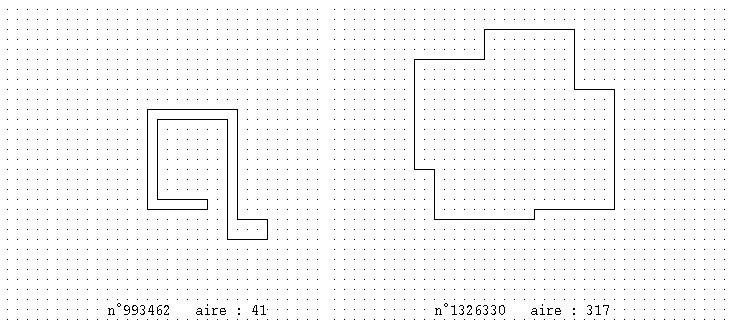
Après beaucoup d'effort, notamment pour éliminer les polygones semblables, le grand Ordix me dit qu'il y a 2200928 polygones distincts dont 11 ont une aire minimale de 41 (tous en forme de serpent), et 8 une aire maximale de 317.
Les deux derniers trouvés:
#10 - 21-06-2011 16:02:19
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
cpnstruction avec 12 murs perpendiculaires
#11 - 21-06-2011 16:53:54
- SHTF47
- Imprnnçbl de Prs2Tt
- Enigmes résolues : 39
- Messages : 1629
- Lieu: Autre nom du colin
Construction avec 12 mrus perpendiculaires


Je ne suis pas sûr que ce soient les extrema... J'ai juste constaté que le périmètre faisait 78 dans tous les cas, et donc que pour le maximum il fallait que la figure fasse comme dimensions 20 par 19, et 12 par 11 pour le minimum...
La musique est une mathématique sonore, la mathématique une musique silencieuse. [Edouard HERRIOT]
#12 - 21-06-2011 17:43:54
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
construction avec 12 myrs perpendiculaires
L'aire mini devrait être atteinte pour un "serpent" le plus fin possible , autre ment dit de largeur 1 avec une portion de largeur 2 la plus petite possible (soit 3 de longueur)
Je ne me vois pas faire moins.
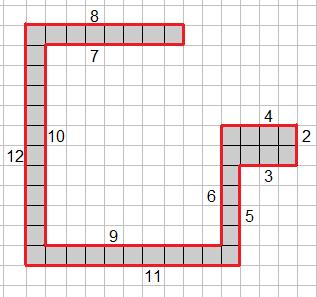
Aire mini 41 , désolé si tu as du recompter.
La somme de 1 à 12 fait 78 , le polygone sera optimisé s'il s'inscrit dans un rectangle 19 x 20.
En rajoutant la condition sur les angles droits, il faut minimiser la partie tronquée.
8*1 7*2 6*3 5*4 ne marche pas
donc 8*2 7*1 6*3 5*4 semble le minimum.
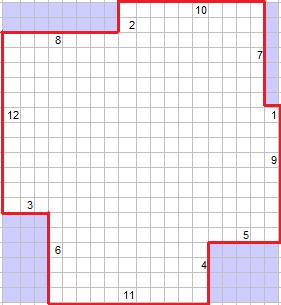
Aire max=319
Un rectangle de base de 18 * 21 = 378 ne permet pas d'améliorer car le minimum troqué serait de 8*1 + 7*2 + 6*3 + 5*4 = 60
#13 - 21-06-2011 19:23:36
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
Construction avec 12 murs peprendiculaires
Arf, je savais bien bien que 5002840/2 ne fait pas 2200928  la dernière "optimisation" de mon programme devait éviter de faire apparaitre des polygones semblable par symétries centrale. En effet en appliquant une symétrie centrale et en inversant le sens de parcours on obtient exactement les mêmes chiffres. Pour résoudre ce problème j'ai bêtement éliminé les solutions dont le deuxième segment part vers le bas au lieu du haut, comme si un parcours qui commence vers le bas ne pouvait se terminer que vers le haut. la dernière "optimisation" de mon programme devait éviter de faire apparaitre des polygones semblable par symétries centrale. En effet en appliquant une symétrie centrale et en inversant le sens de parcours on obtient exactement les mêmes chiffres. Pour résoudre ce problème j'ai bêtement éliminé les solutions dont le deuxième segment part vers le bas au lieu du haut, comme si un parcours qui commence vers le bas ne pouvait se terminer que vers le haut.
Je trouve donc des solutions d'aire 319 (en calculant tout en double  ): ):
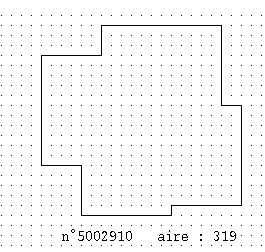
Ce que j'ai dis sur caml était bien entendu une blague, j'aime bien les chameaux, sinon je ne pratiquerais pas 
Le fait est que j'ai toujours eu du mal à déchiffrer les programmes écrits par d'autre donc bon courage à ceux que ça intéresse (J'ai remplacé if m0_2 > 0 par if true dans choix_cote_initial2)
#load "graphics.cma" ;;
open Graphics ;;
open ArrayLabels;;
open List;;
open_graph "1280x1024" ;;
let sgn x = if x>0 then 1 else -1 ;;
let n_trouve = ref 0 ;;
let poubelle _ = () ;;
let rec calcul_air air x y listex listey = match listex,listey with
| (xx::restex) ,(yy::restey) -> let xp = x+xx and yp = y+yy in
calcul_air (air+xp*yy) xp yp restex restey
| _ ,_ -> abs air ;;
let dessine_polygone x0 y0 listex listey =
set_color white ;
fill_rect (x0-250) (y0-250) 500 500 ;
set_color black ;
for i= -20 to 20 do
for j= -20 to 20 do
plot (x0+10*i) (y0+10*j) ;
done ; done ;
moveto (x0-150) (y0-250) ;
draw_string ("n°"^(string_of_int !n_trouve)) ;
draw_string (" aire : "^(string_of_int (calcul_air 0 0 0 listex listey))) ;
moveto x0 y0 ;
let rec dessine x y lx ly = match lx,ly with
| (dx::restex) ,(dy::restey) ->
let xp = x+(dx*10) and yp = y+(dy*10) in
lineto xp y ;
lineto xp yp ;
dessine xp yp restex restey ;
| _, _ -> poubelle ((*wait_next_event [Key_pressed]*)) ; () ;
in dessine x0 y0 listex listey ;;
let polygones_min = ref []
and air_min = ref max_int
and polygones_max = ref []
and air_max = ref 0 ;;
let compare_air listex listey =
incr n_trouve ;
let air = calcul_air 0 0 0 listex listey in
if air <= !air_min
then (if !air_min = air
then polygones_min := (listex,listey):: (!polygones_min)
else (air_min := air ;
polygones_min := [(listex,listey)] ) ;
dessine_polygone 250 500 listex listey )
else ( if air >= !air_max
then (if !air_max = air
then polygones_max := (listex,listey):: (!polygones_max)
else (air_max := air ;
polygones_max := [(listex,listey)] ) ;
dessine_polygone 750 500 listex listey
)
) ;;
let cherche_polygones liste_longeur_cotes =
let moitier = (length liste_longeur_cotes)/2 in
let rec partage cotes1 longeur1 cotes2 longeur2 = function
| a::reste -> if length cotes1 < moitier
then (partage (a::cotes1) (longeur1+a) cotes2 longeur2 reste) ;
if length cotes2 < moitier
then (partage cotes1 longeur1 (a::cotes2) (longeur2+a) reste) ;
| [] -> let rec cherche_signe cotes_prec cotes_signe somme longeur_restante = function
| b::reste ->
if abs somme <= longeur_restante
then (cherche_signe cotes_prec (b::cotes_signe) (somme+b) (longeur_restante-b) reste ;
cherche_signe cotes_prec ((-b)::cotes_signe) (somme-b) (longeur_restante-b) reste )
| [] -> if somme = 0
then if cotes_prec = []
then let prems = hd cotes2 in
cherche_signe cotes_signe [prems] prems (longeur2-prems) (tl cotes2)
else permute_cotes cotes_prec cotes_signe longeur1 longeur2
in let prems = hd cotes1 in
cherche_signe [] [prems] prems (longeur1-prems) (tl cotes1)
and permute_cotes cotes1_signe cotes2_signe longeur1 longeur2 =
let cadrillage = make_matrix (longeur1+1) (longeur2+1) true in
let rec gomme dx dy x y = function
| 0 -> ()
| a_gommer -> cadrillage.(x).(y) <- true ;
gomme dx dy (x-dx) (y-dy) (a_gommer-1)
and trace_cote dx dy x y effectue = function
| 0 -> true
| a_faire ->
if cadrillage.(x).(y) then
(cadrillage.(x).(y) <- false ;
trace_cote dx dy (x+dx) (y+dy) (effectue+1) (a_faire -1))
else (gomme dx dy (x-dx) (y-dy) effectue ;
false )
in
let rec test_permutation deb1 deb2 x y reste1 reste2 = match reste1,reste2 with
| [] ,[] -> compare_air deb2 deb1
| _, _ ->
let rec choix_cote_suivant1 non_choisis1 = function
| [] -> ()
| m1::autre1 ->
let dx = sgn m1 in
if trace_cote dx 0 (x+dx) y 0 (abs m1)
then
(
let rec choix_cote_suivant2 non_choisis2 = function
| [] -> ()
| m2::autre2 ->
let dy = sgn m2 in
if trace_cote 0 dy (x+m1) (y+dy) 0 (abs m2)
then (
test_permutation (m1::deb1) (m2::deb2) (x+m1) (y+m2) (non_choisis1@autre1) (non_choisis2@autre2) ;
gomme 0 dy (x+m1) (y+m2) (abs m2)
) ;
choix_cote_suivant2 (m2::non_choisis2) autre2 ;
in choix_cote_suivant2 [] reste2 ;
gomme dx 0 (x+m1) y (abs m1) ;
) ;
choix_cote_suivant1 (m1::non_choisis1) autre1
in choix_cote_suivant1 [] reste1 ;
in let x0 = (longeur1/2) and y0 =(longeur2/2) and m0 = hd cotes1_signe in
poubelle (trace_cote (sgn m0) 0 (x0+(sgn m0)) y0 0 (abs m0)) ;
let rec choix_cote_initial2 non_choisis2 = function
| [] -> ()
| m0_2::autre2 ->
if true
then (
let dy = sgn m0_2 in
poubelle (trace_cote 0 dy (x0+m0) (y0+dy) 0 (abs m0_2)) ;
test_permutation [m0] [m0_2] (x0+m0) (y0+m0_2) (tl cotes1_signe) (non_choisis2@autre2) ;
gomme 0 dy (x0+m0) (y0+m0_2) (abs m0_2)
) ;
choix_cote_initial2 (m0_2::non_choisis2) autre2 ;
in choix_cote_initial2 [] cotes2_signe ;
in let l0 = hd liste_longeur_cotes in
partage [l0] l0 [] 0 (tl liste_longeur_cotes) ;;
cherche_polygones [1;2;3;4;5;6;7;8;9;10;11;12] ;;
!n_trouve ;;
#14 - 21-06-2011 19:34:29
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Construction avec 122 murs perpendiculaires
298 et 81
306 et 64
308 et 56
309 et 41
314 et 41
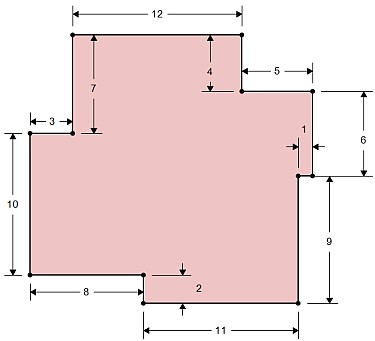
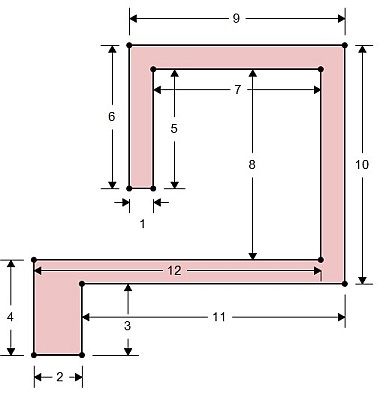
#15 - 21-06-2011 21:24:11
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
Construction avec 12 murs perppendiculaires
Je propose comme aire mini = 58 et maxi = 293 avec les configurations suivantes :
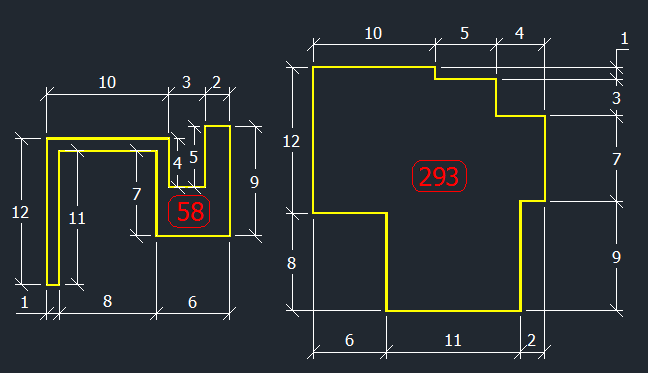
The proof of the pudding is in the eating.
#16 - 22-06-2011 00:35:38
- socato314
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 6
Construtcion avec 12 murs perpendiculaires
L'aire du dodécagone est majorée par 320.
Je n'ai pas mieux que 305...
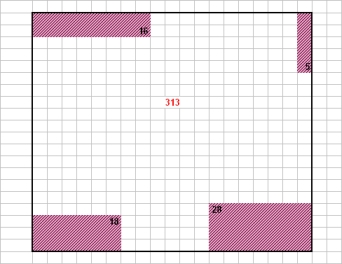
Ébauche de réponse pour la majoration :
Le dodécagone, dont les côtés consécutifs sont deux à deux perpendiculaires, s'inscrit dans un rectangle de même périmètre. Ce rectangle R a donc pour périmètre : 1+2+...+12=78.
Le rectangle d'aire maximale de périmètre 78 et à côtés entiers a pour dimensions 19 et 20.
Si on découpe un coin rectangulaire de R, le polygone restant P1 a 6 côtés. On réitère l'opération avec P1, on obtient 8 côtés, etc..
Il faut donc découper 4 rectangles successifs pour obtenir un dodécagone.
" L'aire du dodécagone est maximale" équivaut à "la somme des aires des 4 rectangles est minimale".
Comme les dimensions de ces rectangles sont 8 des entiers compris entre 1 et 12, l'aire minimale des 4 rectangles est : 1*8+2*7+3*6+4*5=60.
L'aire du dodécagone est donc majorée par 19*20-60=320.
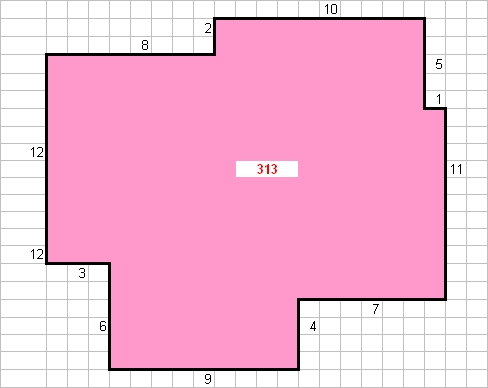
Proposition :
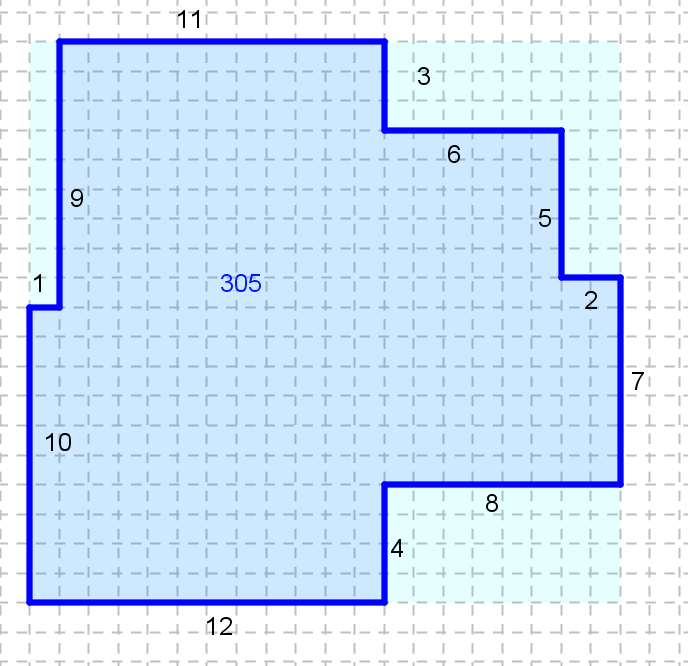
#17 - 22-06-2011 08:25:13
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Construction avec 12 mmurs perpendiculaires
J'ai revu ma copie 
#18 - 22-06-2011 10:19:27
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Construction avec 12 murs perpendiculares
Classement mis à jour à l'heure de ce post, j'espère n'avoir oublié personne difficile de voir les updates 
#19 - 22-06-2011 10:41:45
- SHTF47
- Imprnnçbl de Prs2Tt
- Enigmes résolues : 39
- Messages : 1629
- Lieu: Autre nom du colin
construvtion avec 12 murs perpendiculaires
Je viens de mettre à jour mon aire max. Elle est à 319 maintenant.
J'avoue que c'est plus pratique pour toi si on rajoute un message pour te prévenir de nos changements, plutôt que de modifier notre premier post... 
La musique est une mathématique sonore, la mathématique une musique silencieuse. [Edouard HERRIOT]
#20 - 22-06-2011 11:01:38
- Bamby2
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 152
Constructio avec 12 murs perpendiculaires
bonjour,
je propose 239 pour le grand, et 42 pour le petit:
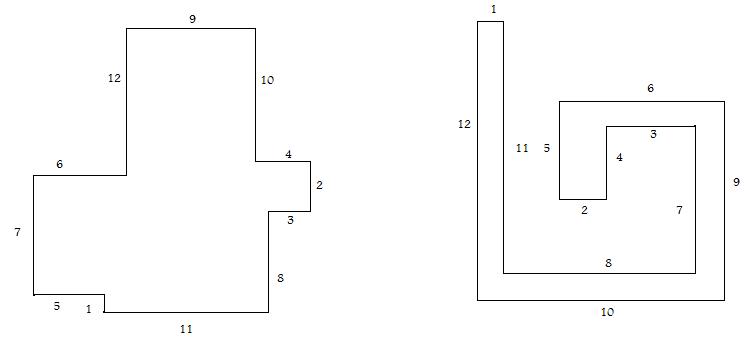
j'ai fait ca au feeling, j'espere que ca sera pas trop nul 
#21 - 22-06-2011 11:07:55
- SHTF47
- Imprnnçbl de Prs2Tt
- Enigmes résolues : 39
- Messages : 1629
- Lieu: Autre nom du colin
Construction avec 12 murs perpendiculaire
Woohooo !! J'suis dans l'top !!

La musique est une mathématique sonore, la mathématique une musique silencieuse. [Edouard HERRIOT]
#22 - 22-06-2011 11:19:29
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1821
construcrion avec 12 murs perpendiculaires
Bonjour !
Optimisation de l'aire maximale à 317 ....
(+4 unités de mieux)
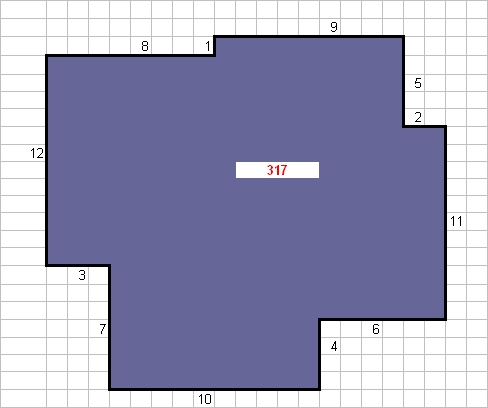
A bientôt,
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#23 - 22-06-2011 18:21:29
- Bamby2
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 152
Construction avec 12 murs perpndiculaires
en reflechissant un minimum j'ai amélioré tout ca:
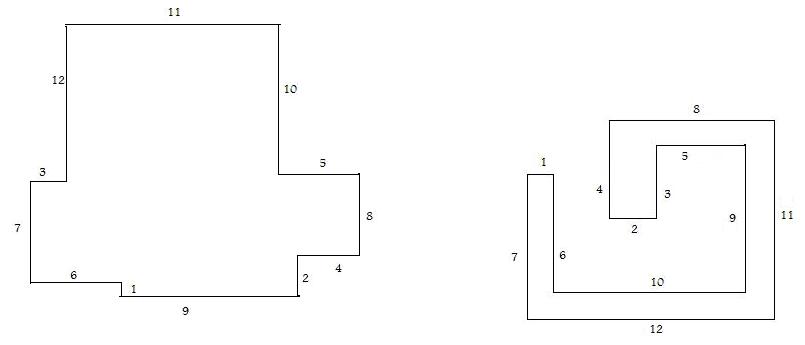
max:280
min: 41
#24 - 22-06-2011 21:06:54
- clementmarmet
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 1329
- Lieu: I'm in spaaaace!!
constryction avec 12 murs perpendiculaires
je pense me tromper, mais je tente quand même 
image
(l'image s'affiche mal...il faut zoomer 'ctrl' + '+' )
EDIT: c'est ce qui me semblais, je me suis planté 
eki eki eki pa tang!!
#25 - 23-06-2011 09:04:49
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
construction avec 12 murs perprndiculaires
Classements mis à jour, j'espère n'avoir oublié personne ^^.
@clementmarmet: Les murs doivent être tous utilisés et une seul fois chacun. L'épaisseur des murs est négligeable. Lorsque je dis qu'on ne peut pas superposer des coins je veux dire qu'il est interdit de faire partir 4murs du même point mais faire partir deux murs du même point est parfaitement autorisé.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum