|
#1 - 25-11-2017 08:20:04
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Une corde et dex murs
Bonjour à tous.
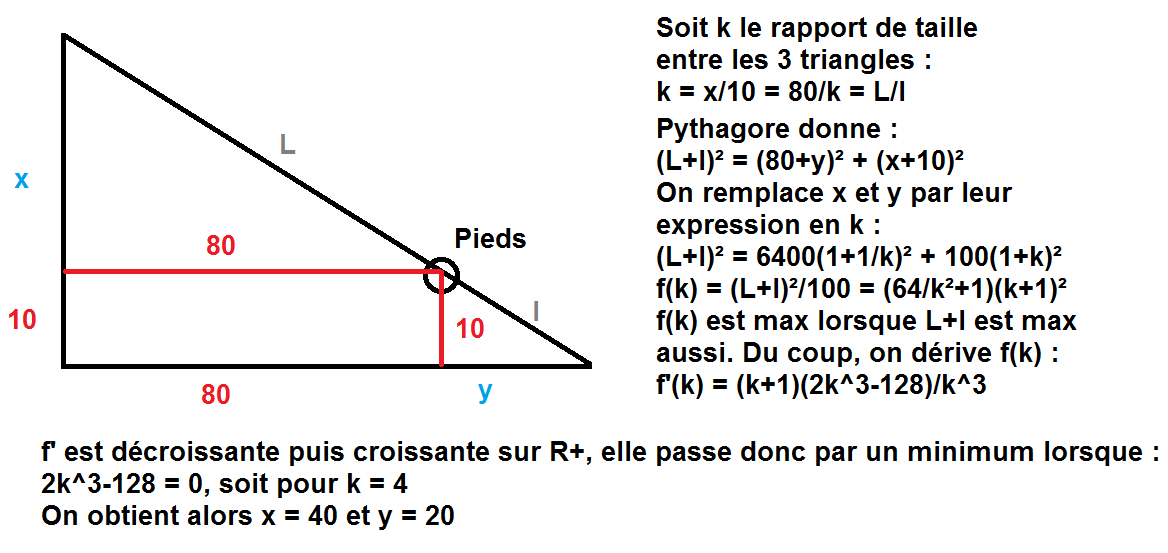
De quelle longueur minimale de corde tendue avez vous besoin pour joindre 2 murs à angles droits, si elle doit passer à vos pieds alors que vous vous trouvez à 10 m d'un mur et à 80 m de l'autre ?
A faire entièrement à la main, sans calculette, longueur arrondie au mètre.
Ne vous égarez pas....
#2 - 25-11-2017 10:41:42
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Une orde et deux murs
Bonjour Nodgim .
A vue d’œil , avec un peu de Thalès : 90√2≈127 m.
Vasimolo
#3 - 25-11-2017 10:56:48
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
une corde zt deux murs
Salut Vasimolo,
Es tu sûr ? Je n'ai pas trouvé pareil. Et ce n'est pas à cause de l'échelle 10 que j'ai rectifiée dans ta réponse.
#4 - 25-11-2017 11:04:46
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
une cirde et deux murs
112 mètres. (racine(12500) exactement... 
en dérivant rac ( (x-10)^2 + 80^2) . x/(x-10) on trouve X = 50
#5 - 25-11-2017 11:05:44
- Bastidol
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 152
nUe corde et deux murs
Bonjour nodgim,
Les murs se croisent on fait passer la corde au plus près de l'intersection.
0 mètres entre les 2 murs ou 81 si le prolongement doit passer à mes pieds.
@+
#6 - 25-11-2017 11:22:30
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Une crde et deux murs
@ Gwen: c'est bien ça. Trop facile là....
Et l'angle alors, en question subsidiaire ?
Et tant qu'on y est, l'angle quelle que soit ta position par rapport aux 2 murs.
@ Batisdol: Je ne sais pas trop dans ce cas comment tu fais pour TENDRE la corde entre les murs. Non, là où tu es, tu dois rester entre les extrémités de la corde.
#7 - 25-11-2017 12:11:15
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Une cored et deux murs
Salut nodgim,
je pose x la longueur telle que sur un mur, la distance entre l'angle des murs et l'attache de la corde fasse (x+80).
Dans ce cas, le théorème de Thalès montre que sur l'autre mur, la distance entre l'angle des murs et l'attache de la corde fait (10+800/x), qui se factorise en (x+80)*10/x.
On cherche donc à minimiser la longueur de la corde, ce qui équivaut à minimiser son carré, qui vaut (x+80)² + ((x+80)*10/x)² = (x+80)² [1+100/x²].
On dérive cette expression : cela donne après simplification 2(x+80)(1-8000/x³). Le dernier facteur se factorise en remarquant que 20 en est une racine : la dérivée est donc 2(x+80)(x-20)(x²+20x+400)/x³.
L'étude du signe de la dérivée montre que la longueur de la corde est minimale pour x=20, ce qui donne une corde de longueur 50*racine(5) (soit environ 112 m).
#8 - 25-11-2017 12:17:28
- Bastidol
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 152
une corde zt deux murs
Faut t'il que la corde soit droite ou la considère tu tendue s'il y a 2 segments?
#9 - 25-11-2017 12:24:48
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Une coorde et deux murs
A faire entièrement à la main, sans calculette
Et tant qu'on y est, l'angle quelle que soit ta position par rapport aux 2 murs
Là, ça devient illusoire de respecter la consigne...
#10 - 25-11-2017 13:05:51
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
une corde et deux muts
@ Ebichu: correct ! tu as suivi le même chemin que celui de Gwen, différent du mien. Je pensais bien que le mien était le seul possible à la main, sans cependant ayant approfondi cette méthode.
@ Batistol: la corde est tendue en ligne droite d'un mur à l'autre. Elle passe juste à tes pieds, en les frolant.
@ Gwen et @ tous :
Le calcul de l'angle cherché est en fait sans doute plus court que la recherche de la longueur directe. L'expression de l'angle cherché est simplissime, si vous trouvez vous comprendrez pourquoi j'ai choisi la position 10 m - 80 m....
#11 - 25-11-2017 13:07:06
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Une crde et deux murs
Pour la question subsidiaire :
en remplaçant 80 et 10 par a et b, le même raisonnement montre que le minimum est atteint pour x=(ab²)^(1/3). La corde mesure alors [a^(2/3)+b^(2/3)]^(3/2) (jolie expression).
Quant à l'angle il mesure arctan((b/a)^(1/3)).
#12 - 25-11-2017 13:50:43
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Une corde e deux murs
Bonjour,
Soit x l'angle entre la corde et le mur dont je suis à 10 m.
La longueur de la corde est : L(x) = 10/sin(x) + 80/cos(x)
La dérivée L'(x) = 10*( 8*(sin(x))**3 - (cos(x))**3 ) / ( (sin(x))**2 * (cos(x))**2 )
s'annule pour x tel que tg(x) = 1/2
D'où :
cos(x) = 2 / sqrt(5)
sin(x) = 1 / sqrt(5)
et L = 50*sqrt(5) = 111.803 m
#13 - 25-11-2017 14:50:14
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
une corde et deyx murs
@ Ebichu : et oui, belles expressions !
ça paye nos efforts quand on arrive à ce genre de formule.
@ Enigmatus: c'est Ok pour toi également, bravo !
#14 - 25-11-2017 15:23:13
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
une coede et deux murs
Ma méthode est un peu bourrin, mais elle devrait marcher.
Point M de coordonnées (80;10) dans un repère orthonormé.
Droite passant par M d’équation: y = a(x–80) + 10
Points muraux de coordonnées (0;10–80a) et (80-10/a;0)
Carré de la longueur de corde: d(a)² = (10-80a)²+(80-10/a)²
Dérivée de d(a)² s’annulant pour: a = -1/2
Soit finalement: d = 50V5 = env. 111,8 m
#15 - 25-11-2017 17:33:55
- Bastidol
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 152
Une corde et deux murrs
ça y est j'ai compris.
Il faut trouver le minimum (la dérivée ) de la fonction y = 10sin( a) + 80cos(a).
mais là j'ai oublié comment faire . Je laisse çà aux matheux.....
#16 - 25-11-2017 17:38:09
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
une corde er deux murs
@ Francky: c'est bien ça, bravo à toi également !
Ta méthode n'est pas si bourrine que ça...
@ Batisdol: il y a une autre approche par Pythagore, mais tu pourras difficilement y arriver sans une petite dérivée...
#17 - 26-11-2017 00:09:20
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
#18 - 26-11-2017 09:02:41
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Une corde et deux muurs
Bien vu Golgot, bravo à toi également !
En cherchant l'angle, tu trouveras l'autre voie....
#19 - 26-11-2017 10:04:18
- Bastidol
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 152
une corde et deux muts
En utilisant un tableur de type EX... je trouve 112m pour un angle de 26,5 °
@+
#20 - 26-11-2017 11:34:10
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Une corde et deux musr
@ Bastidol: c'est la bonne longueur, ce qui était demandé, mais pas tout à fait le bon angle.
Le niveau de ce problème est Lycée, 1ère S.
#21 - 28-11-2017 12:05:23
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Une corde e tdeux murs
Le délai est écoulé.
Les solutions ont été données, que ce soit pour trouver la longueur directement ou en passant par l'angle.
Je rappelle comment on trouve l'angle idéal.
Si on se trouve dans un repère orthonormé avec les droites qui se coupent en (0,0), et si on appelle "x" l'angle cherché, L et H les "x" et "y" du point :
L/cosx + H/sinx est la longueur du segment.
Pour le min, on dérive :
L sinx/cos²x -H cosx/sin²x.
Son annulation est un minimum et donne la solution :
L sin^3 (x) = H cos^3 (x)
tang x = (H/L) ^ (1/3)
D'où le choix du 1/8 pour H/L, qui donne 1/2 pour tang x (pente), de construction facile. La longueur min du segment se calcule alors facilement = V12500 = 112 mètres environ.
Merci à tous pour votre participation.
#22 - 28-11-2017 13:19:27
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Une codre et deux murs
nodgim #21 a écrit:qui donne 1/2 pour tang x, valeur usuelle x = 30°.
tg(30°) = sqrt(3)/3
#23 - 28-11-2017 18:21:09
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Une corde et deux mrs
Heu...oui.
Ou comment aboutir à un calcul correct en confondant sinus et tangente....
Merci Enigmatus, qui a lu avec un oeil critique.
#24 - 28-11-2017 18:46:54
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Une corde te deux murs
On n'aura certainement pas l'angle de façon simple 
J'avais bien trouvé les solutions avec la trigo , Pythagore ou les triangles semblables mais je n'ai pas posté car j'ai tendance à croire qu'il y a une solution élémentaire sans calcul ( je n'ai pas mis le doigt dessus ) .
Vasimolo
#25 - 28-11-2017 23:55:11
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
yne corde et deux murs
Moi aussi j'ai longtemps cherché une solution géométrique qui semblait si évidente mais qui reste introuvable 
|
 |

 Accueil
Accueil
 Forum
Forum