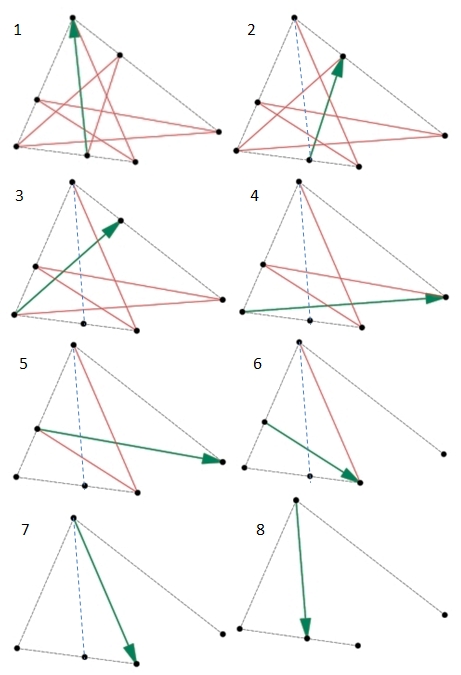
En partant d'un point de l'étoile, et en faisant le tour, (disons en trounant vers la gauche), on tourne à chaque coin d'un angle de [latex]\pi - \theta_i[/latex] (dans le sens trigonometrique), où [latex]\theta_i[/latex] est l'angle aigu positif du [latex]i[/latex]-ème point. Au final, on a fait exactement 3 tours (faire le chemin), donc :
[TeX]3 \times 2 \pi = 7 \pi - \sum \theta_i[/TeX]
et donc
[TeX]\sum \theta_i = \pi[/TeX]
d'ailleurs, il me semble que le problème est le même pour toute étoile du même style (nombre premier de sommets, avec un vrai structure d'étoile bien régulière, notament l'ordre des sommets, ou le fait que chaque branche coupe toutes les autres (sauf celles qui ont un commet commun)). Il suffit d'imaginer que l'on reporte tous les angles de l'étoile parfaite sur un point central pour voir que l'on prend un angle sur deux sur le cerlce : donc [latex]\pi[/latex]. Mathématiquement, on peut montrer que l'on fait [latex]\frac{p-1}{2}[/latex] tours, ce qui donnerait :
[latex]\frac{p-1}{2} 2 \pi = p \pi - \sum_{i=1}^{p} \theta_i[/latex],
d'où :
[latex]\sum_{i=1}^{p} \theta_i = \pi[/latex].
Bref, on fait toujours une somme de [latex]\pi[/latex] !
Accueil
