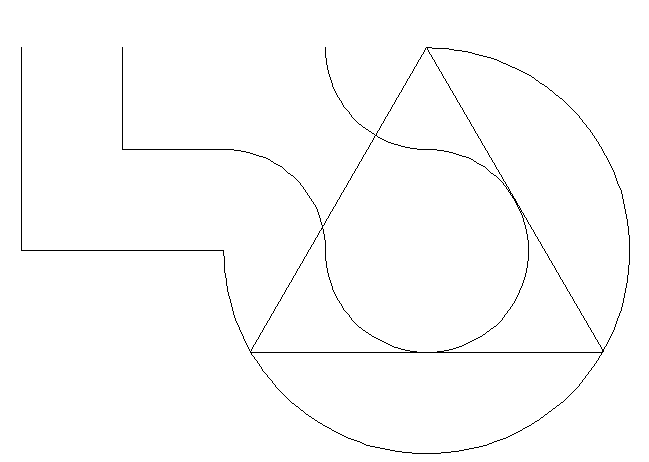|
#1 - 27-07-2010 18:35:42
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Culoir
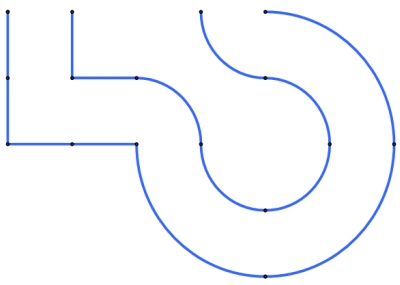
Quelle est la longueur du plus long segment qui peut traverser ce couloir?
(Le dessin est construit à partir d'une grille de mailles 1x1)
#2 - 27-07-2010 19:11:15
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
cpuloir
Un petit essai au hazard [latex]2\sqrt{3}[/latex]
Vasimolo
#3 - 27-07-2010 19:13:57
- EfCeBa
- Administrateur
- Enigmes résolues : ∞+1
- Messages : 11×569
cpuloir
A première vue [latex]2 sqrt 3[/latex].
#4 - 27-07-2010 19:52:55
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Cuoloir
Je dirais que le plus long segment possible part du coin supérieur gauche et part à 45° jusqu'en bas de l'arc de cercle extérieur, ce qui donne un longueur de [latex]4 \sqrt{2}[/latex] cm. Pas sûr, mais ça m'a l'air pas mal 
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#5 - 27-07-2010 21:55:36
- gabrielduflot
- Expert de Prise2Tete
- Enigmes résolues : 34
- Messages : 609
#6 - 28-07-2010 00:31:00
- yoshi2402
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 132
couloie
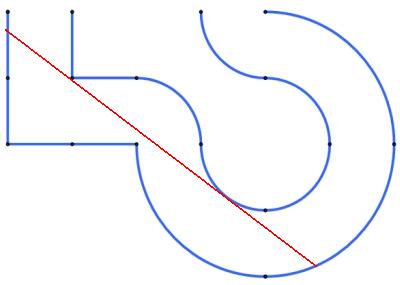
J'affirme sans preuve ni calcul que ce segment est le plus long que l'on puisse tracer dans ce couloir, et je revendique avec fierté mon incapacité à en calculer la longueur!
#7 - 28-07-2010 16:54:44
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Cuoloir
Pour l'instant :
Bonne réponse de Vasimolo et EfCeBa.
Pour les autres, il faut comprendre que par "traverser ce couloir" j'entends "y entrer et en ressortir par l'autre issue". Votre segment va rester coincé 
#8 - 28-07-2010 18:48:48
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Coulloir
"en mathématiques, un segment est une portion de droite." (source : Wikipedia)
Comment un seul segment peut-il traverser tout le couloir ? o_0'
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#9 - 28-07-2010 23:18:19
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
couloie
Le plus long segment qui peut se glisser dans ce corridor mesure 3.41 unités.
Comme le montre la figure ci-dessous, ce segment forme un côté d'un triangle equilatérale dont le noyau central est un cercle inscrit de rayon 1.
L'aire du triangle est, avec c le côté:
[TeX]A=c^2.sqrt(3)/4[/TeX]
et
le cercle inscrit d'un triangle a pour rayon
[TeX]r = 2A/(a+b+c)[/TeX]
avec a = b = c et r=1
ce qui donne [latex]c=2sqrt(3)[/latex]
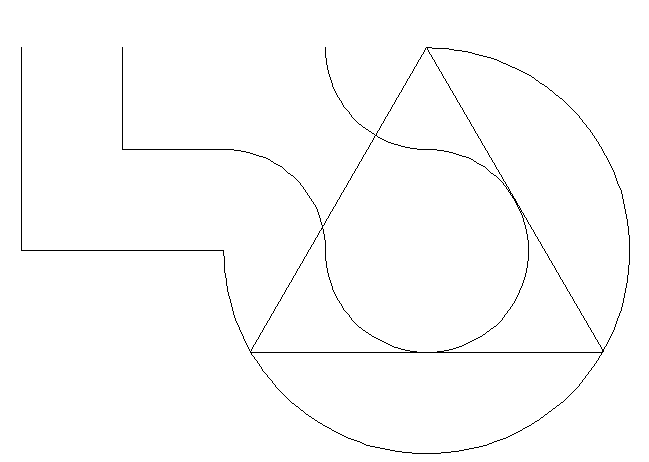
The proof of the pudding is in the eating.
#10 - 30-07-2010 04:40:55
- McFlambi
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 144
couloie
[latex]2\sqrt{3}[/latex] ?
#11 - 30-07-2010 12:15:07
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
couloie
Je pense que la stratégie est lisible sur cette illustration :

Vasimolo
#12 - 30-07-2010 12:46:01
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Coulori
MthS-MlndN a écrit:"en mathématiques, un segment est une portion de droite." (source : Wikipedia)
Comment un seul segment peut-il traverser tout le couloir ? o_0'
Toujours pas de réponse... Je pensais "rebond" version laser-miroirs ou boule de billard sans frottement, mais à ce moment-là mon segment ressort du couloir après deux rebonds à 90°, contrairement à ce que la première réaction de looozer laisse entendre... Alors, quelque chose pour m'aiguiller ?
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#13 - 30-07-2010 14:49:32
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
coukoir
à MthS-MlndN :
Il faut imaginer un menuisier qui porte une planche horizontalement sur son épaule et qui doit progresser dans le couloir pour en ressortir à l'autre bout, tout ça en 2D et vu du dessus (1D pour la planche  ). ).
Sorry pour la réponse tardive!
#14 - 30-07-2010 15:15:53
Cuoloir
Je dirais 2.23 ( sqrt(5) plus precisement)..
#15 - 30-07-2010 15:25:35
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Coulori
Merci beaucoup pour ta réponse 
Dans ce cas, on peut faire entrer n'importe quel segment dans le couloir (à gauche), à 45°, et le passage problématique sera donc le morceau circulaire. Je pense que le segment le plus long qui rentre est celui qui, lorsqu'il est tangentiel au point le plus bas de la portion de cercle intérieure au couloir, touche le cercle extérieur des deux côtés. Un petit coup de Pythagore plus tard, ce segment mesure [latex]2 \sqrt{3}[/latex] soit environ 3,46 cm.
En espérant avoir vu juste 
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#16 - 30-07-2010 16:34:45
- langelotdulac
- Ange de Prise2Tete
- Enigmes résolues : 49
- Messages : 2963
- Lieu: Paradis
ciuloir
Tu es largement assez dingo pour qu'un Minito te semble cohérent \o/ !
#17 - 30-07-2010 18:11:19
- zikmu
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 277
coukoir
un peu moins que 2xracine de 2 sinon ça bloque 
#18 - 30-07-2010 19:04:25
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
couliir
Bravo à Vasimolo, EfCeBa, franck9525, McFlambi et MthS-MlndN pour leur bonne réponse.
Merci à eux et aux autres d'avoir cherché sur ce problème.
Le passage le plus étroit (pour un segment) était la partie entre les deux cercles où, en étant tangent au petit cercle, le segment ne pouvait avoir une taille supérieure à [latex]2sqrt{3}[/latex]. Les dessins de franck9525 et Vasimolo illustrent cette position.
A bientôt! 
Question soulevée par yoshi2402 et illustrée par son dessin :
Pouvez-vous calculer la longueur du plus long segment de droite pouvant entrer entièrement (sans en sortir) dans ce couloir? (il faut un peu d'endurance  ) )
#19 - 30-07-2010 19:22:18
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
coulour
Pour la question subsidiaire de Yoshi : j'avais mon segment de [latex]4 \sqrt{2}[/latex] cm, mais son idée est meilleur. Pour le calcul, euh...
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#20 - 30-07-2010 20:08:40
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
cpuloir
Le dessin de langelot me rappelle un jeu auquel je jouais au collège pendant les cours de langue . On pose la pointe du stylo au début de la piste puis on appuie sur le stylo qui va glisser en laissant une trace sur la feuille , on recommence à l'endroit où le trait quitte la piste ... Pour le parcours proposé on peut s'en sortir avec seulement trois coups de crayons 
Vasimolo
#21 - 30-07-2010 20:46:54
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Coulor
...en étant très adroit (c'est-à-dire après au moins un semestre de philosophie-pour-les-nuls, d'histoire de l'art ou d'espagnol LV3  ) )
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#22 - 31-07-2010 01:13:02
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
couloit
En fait le plus difficile était de surveiller la trajectoire du crayon qui avait une facheuse tendance à quitter la table de "travail" . Moi , en espagnol , je ne jouais pas , je ne travaillais pas non plus , j'étais fou amoureux de ma prof et je planais bêtement sur mon petit nuage 
Nostalgie , nostalgie ...
Vasimolo
#23 - 01-08-2010 16:38:19
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Coloir
Voici ma réponse à la question subsidiaire (longueur de Yoshi) :
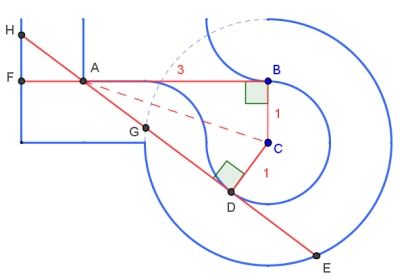
On retrouve la longueur [latex]GE=2sqrt{3}[/latex] citée précédemment et sa moitié [latex]DE=sqrt{3}[/latex].
Par symétrie par rapport à l'axe AC, on sait que AD=3.
Par Pythagore, [latex]AC=\frac{3}{sqrt{10}}[/latex] et donc l'angle BAD vaut [latex]arcos(\frac{3}{sqrt{10}})[/latex].
En réutilisant cet angle dans le triangle rectangle AFH, on trouve [latex]AH=\frac{5}{4}[/latex]
Donc [latex]HE = \frac{17}{4}+sqrt{3}[/latex]
#24 - 01-08-2010 16:56:24
- FRiZMOUT
- Verbicruciste binairien
- Enigmes résolues : 49
- Messages : 2218
Couoir
Ahah, le nul il s'est trompé !
(C'est une symétrie par rapport à l'axe AC...) ^^
#25 - 01-08-2010 17:03:27
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
coyloir
C'est quand même light, comme erreur. Et tu es quelque peu viandard 
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum