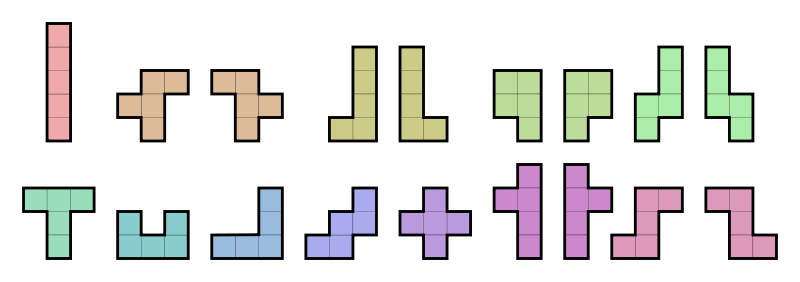Enigme Quadris (super Tetris) @ Prise2Tete

luthin · #1

Vous connaissez tous le jeu Tetris je présume. L'ensemble des pièces de ce jeu est l'ensemble des polygones à angles droits que l'on pourrait dessiner sur le quadrillage d'une feuille et dont la surface S est 4 carreaux. Imaginez le Quadris, la généralisation de Tétris pour S=5. Combien de pièces ce jeu comporterait-il?
Pour l'instant, je n'ai pas de solution quand S est un entier quelconque, si vous avez la solution, et bien vous pouvez la donner aussi!

FRiZMOUT · #2

http://www.research.att.com/~njas/sequences/b000988.txt

MthS-MlndN · #3

Tes "Quadris" s'appellent en fait des pentaminos.

Ils sont utilisés dans une énigme en cours, que je te recommande fortement (elle est excellente) : Un excellent anniversaire de l'ami Arrakis.

Pour n>5, je te renvoie à la page Wikipedia sur les polyominos. Pas tout compris, mais ça a l'air intéressant

Nicouj · #4

Pour S=5, j'en ai compté 18

LeSingeMalicieux · #5

Pour S=5, je crois qu'il suffit de regarder ici

Pour S entier quelconque, le problème est intéressant, mais je vois pas trop comment l'aborder...

Lagaway · #6

Bonjour à tous,

Concernant le tetris classique (S=4), je crois me souvenir qu'il y a 7 formes différentes.

Pour le Quadris (S=5), j'ai dénombré 20 formes :

Pour un tetris encore plus grand : j'ai pas fait !!!

McFlambi · #7

u(1)=1
u(2)=1
u(3)=2
u(4)=7 [tetris]

Pour une formule generale je sais pas... et ca me parait difficile tant les formes peuvent etre complexe au bout d'un moment, sachant que je doute d'une relation de recurrence simple vu comme ca. et qui dit formule simple dit formule de reccurence simple...

Donc je ne me lance pas, et je propose pour u(5) = 18

[5],[4,1]*4,[3,2]*5,[3,1,1]*3,[2,2,1]*3,[2,1,2]*2

mais peut-etre me tromps-je

luthin · #8

McFlambi, je suis d'accord avec toi, pour le cas général, j'ai vite laissé tomber! Sinon, tu as la réponse que j'attendais, tout comme Nicouj et frizmout.
Lagaway, tu as un peu surévalué, tourne un peu la tête...
Mths et LeSingeMalicieux, merci pour l'info, je ne connaissais pas, la célébrité, ça ne sera pas pour cette fois!

Lagaway · #9

Oups ! En effet, je me suis laissé emporter par la construction de ces petites formes carrées...

ça devrait être bon à présent (enfin j'espère) :

Donc 18 !

rivas · #10

Les pièces s'appellent des pentaminos (parfois pentominos). Il y a une littérature plus qu'abondante sur le sujet.
Point de départ habituel: Google ou http://fr.wikipedia.org/wiki/Pentamino

Pour ta question: Il y en a 12.

Pour S plus grand, un certain nombre sont disponibles ici:
http://villemin.gerard.free.fr/Puzzle/minoPoly.htm#top

MthS-MlndN · #11

Lagaway a écrit:
Pour le Quadris (S=5), j'ai dénombré 20 formes

Il m'a fallu à peu près dix minutes pour enfin comprendre pourquoi tu en avais deux de trop, alors que deux posts plus loin, tu donnais toi-même la réponse o_0'

luthin · #12

Merci à tous, la réponse que j'attendais était 18.

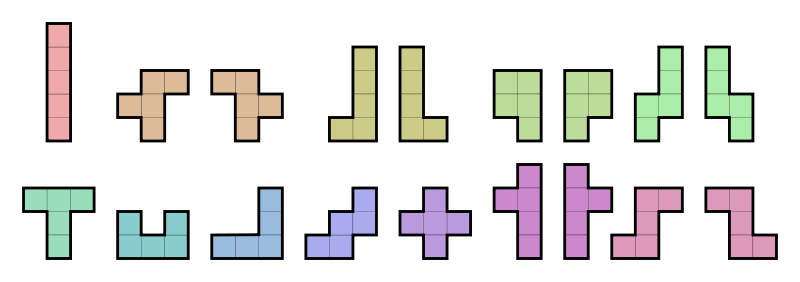
Comme dans le jeu Tetris, deux pièces sont différentes si elles sont l'image l'une de l'autre dans un miroir et identiques si elles sont l'image l'une de l'autre par une rotation. Ceux qui ont donné 12, n'ont pas tenu compte de la première contrainte.
D'après Wikipedia, il s'agit de polyominos (ici des pentaminos) à un seul coté et la liste des dénombrements peut se trouver ici.
A l'heure actuelle, on ne sait toujours pas faire le dénombrement pour S quelconque, la question subsidiaire, était donc un sujet de recherche (désolé, je ne le savais pas)!

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 10-10-2010 23:44:08

Quadris (super Tetrsi)

#0 Pub

#2 - 11-10-2010 01:28:27

uQadris (super Tetris)

#3 - 11-10-2010 09:36:09

Quardis (super Tetris)

#4 - 11-10-2010 11:47:52

Quaddris (super Tetris)

#5 - 13-10-2010 08:39:33

Quaris (super Tetris)

#6 - 13-10-2010 11:27:35

Quaris (super Tetris)

#7 - 13-10-2010 18:31:47

Quadris (superr Tetris)

#8 - 13-10-2010 19:00:02

quadris (supet tetris)

#9 - 14-10-2010 02:45:17

uQadris (super Tetris)

#10 - 14-10-2010 22:56:39

Quadris (super eTtris)

#11 - 15-10-2010 09:26:16

Quadris (usper Tetris)

Lagaway a écrit:

#12 - 15-10-2010 10:42:37

Qaudris (super Tetris)

Réponse rapide

Sujets similaires

Mots clés des moteurs de recherche

Pied de page des forums