Enigme Le jeu du 1 @ Prise2Tete

Yannek · #1

On considère le jeu suivant :

(1) On commence avec un score nul.
(2) On lance un dé (à six faces numérotées de 1 à 6, équilibré). Si le résultat est 1, le score est ramené à 0 et la partie est finie (étape 4). Sinon, le résultat est ajouté au score du joueur.
(3) Le joueur peut alors décider d'arrêter la partie (étape 4) ou de relancer le dé (étape 2).
(4) La partie est finie, le joueur note son score.

Question 1 Vous pouvez jouer une partie. Chaque point vous rapporte un euro. Comment jouez vous pour obtenir un gain optimal ? (expliquez quelle décision vous prenez au coup de dé numéro N avec un score de S)

Question 2 (un peu plus difficile) On modifie un peu les règles. Il vous faut décider à l'avance au bout de combien de lancers vous vous arretez. Quel nombre choisissez vous ?

Question 3 (encore plus difficile) On revient aux règles initiales, mais vous jouez contre un autre joueur, alternativement. (le premier joueur lance un dé, puis le second, puis le premier -s'il n'est pas éliminé ou s'il n'a pas arrété-, puis le second, -s'il n'est pas éliminé ou s'il n'a pas arrété-,etc...). Le vainqueur est celui qui termine avec le plus haut score (en cas d'égalité, le premier qui s'est arrêté).
Que décidez vous de faire au coup N, avec un score S et un score de l'adversaire S' ?

Si vous le pouvez, justifiez vos choix !

Précision. dans la question 3, si l'un des joueurs arrete, l'autre peut continuer à jouer tant qu'il le souhaite (et qu'il n'obitent pas 1)

Klimrod · #2

Bonjour,

Question 1 : chaque résultat de lancer étant indépendant de ce qui s'est passé auparavant, la stratégie à mettre en place ne dépend donc pas du nombre N de lancer, seulement du score S déjà atteint.
Il faudra continuer de jouer si et seulement si l'espérance de gain est supérieure au gain déjà amassé.
Le gain déjà amassé est S.
L'espérance de gain est 1/6 * 0 + 1/6 * (S+2) + 1/6 * (S+3) + 1/6 * (S+4) + 1/6 * (S+5) + 1/6 * (S+6)
Donc 5/6*S + 20/6 > S
Donc 5S + 20 > 6S. Donc S < 20

Tant que l'on n'a pas atteint le score de 20, on continue de jouer. A 20, on décide comme on veut, et au-delà de 20 on arrête.

Question 3 : si mon score S est inférieur ou égal à celui de mon adversaire, évidemment je continue !
La question revient à chercher le tirage probable de l'adversaire au coup suivant et de déterminer si j'ai suffisamment d'avance.
Mon avance = S - S'
Le tirage probable de l'adversaire au coup suivant = 1/6 * 0 + 1/6*2 + 1/6*3 + 1/6*4 + 1/6*5 + 1/6 * 6
Donc S-S' > 1/6 * 20
Donc S-S' > 3,33

Dès que j'ai 4 points d'avance (ou plus) sur mon adversaire, j'arrête de jouer. Tant que j'ai moins de 4 points d'avance (ou que je suis en retard), je continue.

Question 2 : j'ai un peu la flemme de faire les calculs, alors très grossièrement je me dis que l'espérance de tirage étant de 3,33 et l'équilibre stratégique étant à 20 points, je choisis de lancer 6 fois le dé.

Si j'ai tout faux, je vais me ridiculiser
Klim.

Milou_le_viking · #3

Question 1:
Soit G l'espérance de gain et S le score obtenu, alors :
[TeX]G=\frac{2+3+4+5+6}{6}-\frac{S}{6}[/TeX]
Je joue tant que l'espérance de gain est positive, càd tant que,
[TeX]S\leq 20[/TeX]
Quand le score est inférieur à 20, je joue encore, quand il est supérieur, j'arrête et quand il est égal à 20, je fais ce que je veux puisque j'ai la même espérance de gain.

Question 2:
Il faut associer une espérance de gain à chaque valeur de N. L'espérance de Gain la plus élevée correspond au nombre de lancé optimal.
[TeX]G_1=\frac{20}{6}=3,3...3[/TeX][TeX]G_2=...[/TeX]
Là, je dois encore chercher.

Après 1 jet de dé, il y a 5 combinaisons gagnante et une perdante. Chaque combinaison a une probabilité de 1/6.
Après 2 jets de dé, il y a 25 combinaisons gagnants et 11 perdantes (en supposant qu'on relance même si on a perdu, ça ne change rien puisqu'on a perdu). Chaque combinaison a une probabilité de (1/6)².
Après n jets de dé, il y a 5^n combinaisons gagnantes et 6^n-5^n combinaisons perdantes. Chaque combinaison a une probabilité de (1/6)^n.
[TeX]G_1=\frac{20}{6}=3,33...3[/TeX]
avec
[TeX]\sum_{a=2}^{6}a=20[/TeX][TeX]G_2=\frac{200}{6^2}=5,55...5[/TeX]
avec
[TeX]\sum_{a=2}^{6} \sum_{b=2}^{6}(a+b)=200[/TeX][TeX]G_n=\frac{F(n)?}{6^n}[/TeX]
avec
[TeX]F(n)=\sum_{a=2}^{6} \sum_{b=2}^{6}\ ... \sum_{n=2}^{6}(a+b+...+n)[/TeX]
Où F(n) est la somme de tous les gains en n lancés de dé.

Et je ne suis pas sûr que la notation soit correcte.

Je trouve encore ça :
[TeX]G_3=\frac{1500}{6^3}=6,944...4[/TeX]
Mais il faut que je trouve un moyen de calculer les autres.

Ah si! Peut-être ceci :
[TeX]F(n)=\sum_{a=2}^{6} \sum_{b=2}^{6}\ ... \sum_{n=2}^{6}(a+b+...+n)= 5^{(n-1)}.20n[/TeX]
Ce qui donne :
[TeX]G_4=\frac{5^3.80}{6^4}=7,716[/TeX][TeX]G_5=\frac{5^4.100}{6^5}=8,038[/latex]<-

[latex]G_6=\frac{5^5.120}{6^6}=8,038[/latex]<-

[latex]G_7=\frac{5^6.140}{6^7}=7,814[/TeX]
L'espérance de gain est optimale pour 5 ou 6 lancés de dé.

D'ailleurs l'espérance de gain est plus joliment écrite comme ça :
[TeX]G_n=(\frac{5}{6})^{(n-1)}\ \frac{20}{6}n[/TeX]
Question 3:

42

Nicouj · #4

Si j'ai gagné S, alors je peux espérer gagner 1/6*0+(S+2)/6+(S+3)/6+(S+4)/6+(S+5)/6+(S+6)/6 = (5S+20)/6. Soit plus de S si S est inférieur à 20.

SI je joue n fois j'ai (5/6)^n chances de gagner de l'argent.
A chaque fois que je ne tire pas un 1, je peux espérer gagner (2+3+4+5+6)/5=4
Donc je peux espere gagner (5/6)^n*4*n. Le max est atteint pour n=5 n=6.

scarta · #5

1) Pour un gain actuel S, mon gain au lancer suivant est
S' = (-S+2+3+4+5+6)/6 = (20-S)/6 < 0 pour S > 20
Conclusion: pour un gain inférieur à 20, je tente le coup de continuer

2) La probabilité de ne pas voir un 1 sur N lancers est (5/6)^N. Cette probabilité est supérieure à 1/2 pour n <= -ln(2)/ln(5/6) = 3,8
La probabilité de perdre après 3 lancers est donc supérieure à 1/2.
D'un autre côté, le gain moyen à 3 lancers est de 6.94 contre 7.72 à 4 lancers (et redescend ensuite). Je choisis donc 4 lancers.

3) Si l'adversaire ne joue plus, je continue tant que S <= S'
Sinon, faut que j'y reflechisse

dylasse · #6

Question 1 :

Soit S la somme à notre disposition, après le coup suivant notre cagnotte sera de 0 (1 chance sur 6), de S+2 (1/6), de S+3 (1/6).. ou S+6 (1/6).
L’espérance de la cagnotte à l’issue du coup suivant est donc de (5S+20)/6.
Il faut continuer si S<(5S+20)/6, soit S<20.
Rem : cette décision n’est pas fonction du nombre de coups déjà joués.

Question 2 :

Nous allons prendre les notations suivantes :
P(n) : probabilité de ne pas être à 0 après le coup n.
E(n) : espérance du montant de la cagnotte après le coup n
V(n) : valeur moyenne de la cagnotte après n si le 1 n’est jamais sorti.

P(n+1)=P(n)*5/6 : on a 5 chances sur 6 à chaque coup de ne pas faire 1. Donc, P(n) = (5/6)^n.
V(n+1) = V(n) + (2+3+4+5+6)/5 = V(n)+4. Donc V(n) = 4n.

E(n) = V(n) * P(n) + 0 * (1-P(n))= 4n (5/6)^n.

Il faut continuer à jouer tant que E(n) est croissante.

Etudions la fonction E(x)=4x (5/6)^x.

E(x) = 4x exp(x ln(5/6))
E’(x) = 4 exp (x ln(5/6)) + 4 x ln(5/6) exp(x ln(5/6)) = 4 exp (x ln(5/6)) (1+x ln(5/6))
La dérivée de E(x) s’annule pour x = 1/ln(6/5) ~ 5,48.

Donc l’espérance de gain est maximum pour n=5 ou n=6.
E(5)=20 (5/6)^5
E(6)=24 (5/6)^6=24*5/6*(5/6)^5=20 (5/6)^5.
L’espérance de gain est donc maximale après le coup 5 ou le coup 6 (il y a égalité). Comme en bourse, les plus prudents choisiront de s’arrêter après le coup 5, les plus téméraires après le coup 6. L’espérance est la même, par contre au bout de 6 coups il y a moins de chance d’avoir une cagnotte non vide (p(6)<p(5)) mais si on n’est pas à zéro, les gains sont supérieurs (V(6)>V(5)).

Question 3.

Dans un jeu à 2, il y a des situations évidentes :
On s’arrête si l’autre s’est arrêté avant avec une cagnotte inférieur à la nôtre (si l’autre applique la même stratégie, il ne s’arrêtera pas dans ces conditions, sauf évidemment contraint par un zéro).
On continue si l’autre a une cagnotte supérieure à la nôtre (qu’il se soit arrêté ou non).

Il reste à déterminer dans quelle circonstance on va décider de s’arrêter si notre cagnotte est supérieure à celle de l’autre. On conçoit bien que le nombre de coups déjà joués n’a pas d’importance et que seul l’écart D entre nous et l’adversaire a une importance pour prendre notre décision.

Si je m’arrête, calculons la probabilité de ne pas perdre : Pa. Il va falloir n coups pour être dépassé (car en cas d’égalité, j’ai gagné, puisque je me serais arrêté avant), où V(n)>D, donc 4n>D, donc n>D/4. n est le plus petit entier strictement supérieur à D/4, que l’on va noter n(D)=ent(D/4)+1.
la probabilité pour que l’adversaire soit à zéro avant de m’avoir rejoint est Pa = 1 – p(n(D)) = 1 – (5/6)^(ent(D/4)+1).
Si on continue, la probabilité de ne pas perdre au tour suivant est : Pc = 5/6.

Je vais donc décider de continuer si la probabilité de ne pas perdre au tour suivant* est supérieure en continuant plutôt qu’en arrêtant : Pa<Pc.
* la notion de tour suivant s’applique, si je m’arrête, à la série de mon adversaire puisque je n’ai plus l’occasion de rejouer.

Je vais donc continuer tant que 1 – (5/6)^(ent(D/4)+1) < 5/6,
Soit ent(D/4) < ln(1/6)/ln(5/6)-1~8,82
Soit ent(D/4)<=8
Soit D<=35

Ce qui signifie que tant que l’écart que j’ai avec mon adversaire est inférieur ou égal à 35, je continue.
Et je me pose la question à chaque fois…

Je suis surpris par cette valeur d’écart que je trouve très élevée, mais comme j’ai du mal à identifier la faille (comme j’ai du mal d’ailleurs à me convaincre de la justesse du raisonnement !), je poste cette démonstration, qui permettra peut-être d’alimenter les discussions…

NickoGecko · #7

Bonjour,
Merci pour cette énigme "proba" ...

Hmm, les probabilités avec "risque" de s'arrêter à chaque itération me laissent toujours perplexe, pour le dénombrement des coups "perdants".
= doit-on considérer des tirages "fictifs" au coup N+1 si le coup N est perdant, ou raisonner sur les tirages réels, puisque si le coup N est perdant alors pas de tirage N+1 ?

En partant sur l'hypothèse "pas de tirages N+1 si N perdant", je me suis lancé bille en tête dans une simulation sur les 4 premiers coups en cumulant les scores :

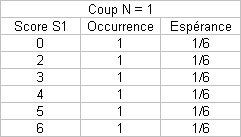
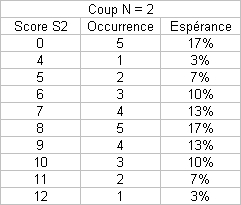
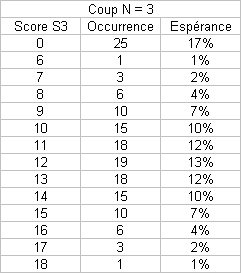
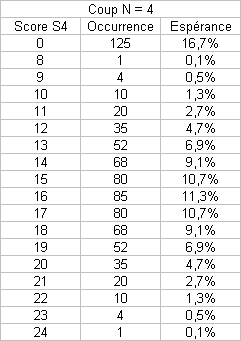
Pour enfoncer une porte ouverte : à chaque coup, la probabilité (ou espérance) de faire 1, et donc de perdre, est 1/6, quel que soit l'historique, donc quels que soient le nombre de coups N ou le score cumulé S.

La suite définissant les occurrences des scores non nuls au coup N+1 est intéressante aussi, c'est une sorte de triangle de Pascal glissant effectuant la somme d'au plus 5 termes (somme des occurences de rang i-5 > 0 à i) des des occurrences du coup N....

Donc en l'absence de mise de départ à chaque partie, voire croissante à chaque coup, si il est possible de faire plusieurs parties d'affilée, je ne jouerai qu'un seul coup et capitaliserai ainsi les gains dans 5 cas sur 6, ou au pire, pas de progression.

Je serai intéressé par les réponses ! Merci pour cette P2T !

A suivre ....

rivas · #8

Enigme intéressante. Je n'ai pas beaucoup de temps en ce moment mais je ne voulais pas ne pas du tout répondre.

Par contre je suis assez confusionné par le fait qu'il n'y a pas de mise fixe à chaque coup. On ne peut donc que gagner... Cela me pose des problèmes pour les questions 2 et 3.

La Question 1 est assez simple. Si a un instant t, on possède une somme S, l'espérance de gain au coup suivant est -S/6 (le 1 sort) + 1/6(2+3+4+5+6) (les autres chiffres sortent). A chaque coup, on joue si l'espérance de gain est >= 0 c'est à dire si S est <= 20. Au delà on risque de plus perdre que de gagner il faut donc s'arrêter. Je ne vois pas en quoi cela dépend de N??

Pour les questions 2 et 3 je vais réfléchir encore un peu et essayer de répondre avant la fin du temps.

Question 3:
Si S'=0 (l'autre joueur est éliminé), on s'arrête: quel que soit S on a gagné.
Si S<S' on joue sinon on a perdu à coup sûr (que l'autre joueur ait arrêté ou pas).
Si S>=S' et l'autre joueur a arrêté, on s'arrête et on a gagné.
Il ne reste donc que le cas S>=S' et l'autre joueur n'a pas encore arrêté. La question est doit-on arrêter ou continuer?
Si on arrête, l'autre joueur va continuer à jouer jusqu'à ce que son score soit au moins égal au notre (sinon il a perdu) ou qu'il perde en tirant un 1. La probabilité qu'il perde en tirant un '1' dans une séquence de Q coups à jouer est de P(Q)=1-(5/6)^Q. Mais il ne compare pas cette valeur à 1/2 car s'il ne continue pas, il va perdre, c'est certain. Donc il continue jusqu'à ce qu'il tire un '1' ou dépasse ou atteigne notre score. A chaque tour auquel il ne perd pas, il gagne en moyenne: (2+3+4+5+6)/5 points soit 4 points.
Pour prendre notre décision de continuer ou pas, on calcule qu'il doit donc jouer encore au moins Q=E((S'-S+3)/4) coups (arrondi au multiple de 4 supérieur puis division par 4, E(x) est la partie entière de x). On calcule P(Q)=1-(5/6)^Q et si sa probabilité de gagner est >= 1/2 on doit continuer de jouer. La difficulté ici vient que notre stratégie doit être basée sur la probabilité de gagner du joueur adverse et non sur la notre.
Avec cette stratégie, les 2 joueurs continuent de jouer jusqu'à ce qu'un des joueurs tire un '1' auquel cas l'autre s'arrête ou que l'écart de leur score deviennent assez grand auquel cas le joueur avec le plus grand score s'arrête en espérant que l'autre joueur qui continue jusqu'à atteindre ou dépasser le score et s'arrêter immédiatement tire un '1' avant d'atteindre son score.

Concrètement P(Q) < 1/2 pour Q > 3,8 (=ln(1/2)/ln(5/6)).
Donc en jouant 4 coups, on a plus de chances de tirer au moins une fois un '1' que de ne pas en tirer du tout. Il faut donc s'arrêter dès que l'on a 13 points d'avance. Cela nécessite à priori 4 coups à 4 de moyenne pour être rattrapé. L'autre joueur à plus de chances de perdre que de gagner en jouant ces 4 coups et chaque coup supplémentaire pour nous augmente notre chance de perdre.

Le raisonnement consistant à prendre 3*6+1 pour être sûr qu'en 3 coups on ne peut être rejoint n'est pas correct car on risque soit même de perdre avec un probabilité >1/2 pour atteindre cet écart supplémentaire.

J'espère que ma démo de la Question 3 vous convaincra.
Merci pour cette énigme.

Yannek · #9

Un petit état des lieux des réponses :

- une tentative prometteuse au tableur de Nicogecko

- Question 1 : Ok pour Klimrod, Milou, Scarta, Dylasse, Nicouj et Rivas (toutes les réponses sont argumentées, en plus !)

- Question 2 : Ok pour Milou, Dylasse, Nicouj. (Klimrod, ton raisonnement ne me semble pas correct. Scarta, j'ai le même raisonnement, mais la suite que tu considères ne décroît pas au moment où tu l'affirmes.)

- Question 3 : Milou est sous l'influences de Douglas Adams. Ça ne marche pas.
Après une lecture sommaire (je peux me tromper), je ne suis pas d'accord avec les raisonnement de Dylasse et Rivas (même si j'ai presque la même chose que toi, Rivas) :
Spoiler : [Afficher le message]
En tout cas, ma réponse à la question 3 est assez fastidieuse (ce qui veut dire qu'on peut l'expliquer mieux ?)

Milou_le_viking · #10

Pour la dernière question, les joueurs lancent les dés alternativement ou un joueur peu jouer plusieurs coups d'affilés pour rattraper son adversaire que à prit de l'avance au score ?

Un joueur qui a arrêté à un tour, peut-il rejouer au tour suivant s'il s'est fait dépasser par son adversaire ?

Je me lance quand même dans une solution, en supposant que la décision d'arrêter est définitive et que l'adversaire n'a plus droit qu'à un coup pour gagner.

C'est à moi de jouer avec un score S contre un score de S' pour mon adversaire.
Soit P(G) la probabilité que l'adversaire gagne au prochain tour et P(N), la probabilité qu'il fasse un match nul au prochain tour.
Il y a 9 cas en tout:
Si S-S'<0, je suis obligé de jouer sinon j'ai perdu.
Si S-S'=0, les scores étant symétriques, il me semble que les chances sont égales quelle que soit la décision. (je dois vérifier ça)
Si S-S'=1 et que j'arrête, P(G) = 5/6 et P(N) = 0.
Si S-S'=2 et que j'arrête, P(G) = 4/6 et P(N) = 1/6.
Si S-S'=3 et que j'arrête, P(G) = 3/6 et P(N) = 1/6.
Si S-S'=4 et que j'arrête, P(G) = 2/6 et P(N) = 1/6.
Si S-S'=5 et que j'arrête, P(G) = 1/6 et P(N) = 1/6.
Si S-S'=6 et que j'arrête, P(G) = 0/6 et P(N) = 1/6.
Si S-S'>6, je ne lance pas de dé et j'ai gagné puisque l'adversaire n'a aucune chance de revenir au score en un coup.

A ces probabilités, il faut comparer la probabilité que je perde à ce tour si ce joue. J'ai une probabilité de 1/6 de perdre et une probabilité de 5/6 d'améliorer mon score et donc d'accroitre la différence S-S'.

Pour S-S' = 4, j'ai 1/6 de perdre, ou lui 1/36 de faire nul. Dans les autres, je tue l'adversaire.
Je risque 1/6 de perdre pour lui retirer 11/36 de gagner. Donc je dois jouer ainsi que pour les valeur inférieure à S-S'=4 afin de réduire les chance de victoire de l'adversaire.

Pour S-S' = 5, j'ai 1/6 de perdre, ou lui 0/36 de gagner et 1/36 de faire nul.
Je risque 1/6 de perdre contre sa probabilité de victoire qui passe de 1/6 à 0/6 et je réduis ses chances de nul.

Pour S-S' = 6, j'ai 1/6 de perdre ou il a perdu. Je lui offre donc une possibilité de gagner alors qu'il n'avais plus qu'une chance de nul.

Donc, je joue quand S-S' < 6.

Yannek · #11

Question 1.
Comme tout le monde l'aura noté, l'espérance de gain ne dépend que du score et pas du numéro du coup joué :
[TeX]{\mathbb E}(G)=\frac{2+3+4+5+6}6-\frac S6=\frac{20-S}6[/TeX]
Donc tant que S<20, on continue de jouer, on fait ce que l'on veut pour S=20 et on s'arrète dès que S>20.

Question 2.
L'espérence de gain au bout de n coups est le produit de la proba de ne pas avoir fait 1 avec n fois le gain moyen d'un coup sans 1 (qui est de 4) :
[TeX]{\mathbb E}(n)=4n\left(\frac 56\right)^n[/TeX]
Cette expression s'étend en une fonction définie pour les réels x, dérivable de dérivée :
[TeX]{\mathbb E}'(x)=4(x\ln\frac 56+1)\left(\frac 56\right)^x[/TeX]
On en déduit que E est minimale en a=-1/(ln(5/6)) avec 5<a<6. On constate que
[TeX]{\mathbb E}(5)=4\times\frac{5^6}{6^5}={\mathbb E}(6)[/TeX]
Donc on décide de jouer indifférement 5 ou 6 coups.

Question 3.
La décision ne dépend que de la différence de score entre mon adversaire et moi.

On note Q(n) la proba que l'adversaire fasse 1 après avoir obtenu un score de n exactement. Derrière chaque Q(n) de la liste suivante on présente entre crochet les combinaisons obtenues avant d'avoir 1 assorties de leurs probas. La somme de ces probas multipliée par la proba d'avoir 1 au dernier coup (1/6) donne Q(n).

Code:

Q(0)=1/6 ([]:1)
Q(1)=0 ()
Q(2)=1/36 ([2]:1/6)
Q(3)=1/36 ([3]:1/6)
Q(4)=7/216 ([4]:1/6,[22]:1/36)
Q(5)=1/27  ([5]:1/6,[32]:2/36)
Q(6)=55/1296 ([6]:1/6,[42]:2/36,[33]:1/36,[222]:1/216))
Q(7)=1/48 ([52]:2/36,[43]:2/36,[322]:3/216)
Q(8)=217/7776 ([62]:2/36,[53]:2/36,[44]:1/36,[422]:3/216,[332]:3/216,[2222]:1/1296)
Q(9)=13/486 ([63]:2/36,[54]:2/36,[522]:3/216,[432]:6/216,[333]:1/216,[3222]:4/1296)
Q(10)=1249/46656 ([64]:2/36,[55]:1/36,[622]:3/216,[532]:6/216,[442]:3/216,[433]:3/216,[4222]:4/1296,[3322]:6/1296,[22222]:1/7776)
Q(11)=1205/46656 ([65]:2/36,[632]:6/216,[542]:6/216,[533]:3/216,[443]:3/216,[5222]:4/1296,[4322]:12/1296,[3332]:4/1296,[32222]:5/7776)
Q(12)=6535/279936 ([66]:1/36,[642]:6/216,[633]:3/216,[552]:3/216,[543]:6/216,[444]:1/216,[6222]:4/1296,[5322]:12/1296,[4422]:6/1296,[4332]:6/1296,[3333]:1/1296,[42222]:5/7776,[33222]:10/7776,[222222]:1/46656)
Q(13)=83/3888 ([652]:6/216,[643]:6/216,[553]:3/216,[544]:3/216,[6322]:12/1296,[5422]:12/1296,[5332]:12/1296,[4432]:12/1296,[4333]:4/1296,[52222]:5/7776,[43222]:20/7776,[33322]:10/7776,[322222]:6/46656)

La probabilité P(n) de gagner en s'arrêtant avec une avance de n est donc donnée par la somme des Q(k) pour k<n+1. Elle est clairement une fonction croissante de n. Or
[TeX]P(12)\approx 0.48554,\qquad P(13)\approx 0,50688[/TeX]
Donc je continue à jouer jusqu'à ce que j'ai 13 points de plus que mon adversaire.

Il s'agit de la stratégie optimale. Est-elle nettement meilleure que de s'arrêter à 12, 35, 42 ou de ne jamais s'arrêter ? Non. En jouant avec cette stratégie, je décide de m'arrêter seulement 2 parties sur 1000 (et oui, c'est super rare d'avoir 12 points d'avance sans que personne n'ai obtenu 1). Et sur ces deux parties sur 1000, j'ai seulement un avantage de 1.4% chances de gain par rapport à mon adversaire...

Autant dire qu'on ne voit pas, en simulant des millions de parties, de différences nettes de résultat entre ces différentes stratégies...

En revanche, en s'arrêtant avant 7, la différence est clairement visible.

Merci aux participants,
Yannek.

kosmogol · #12

Je connaissais ce jeu sous le nom de "101 (sans 1)" avec comme objectif d'être le premier à arriver à 101. Mais je n'avais jamais chercher à optimiser ! Merci.

Bamby2 · #13

j'ai un peu de mal avec les proba, mais pour la question 2 je m'arreterai au feeling au lancé 5(ou 6):
a chaque lancé n, je peux soit gagner une somme E,
soit perdre n-1 fois mes gains précédent (n-1)*E,

donc au lancé 6 mon espérance est:
5/6*E - 5E*1/6 = 0

pour la question 1:
quel que soit le numéro du lancé, mon gain est E=20/6,
et ma perte est le total accumulé /6
donc je doit avoir
20/6>Total*1/6 donc je continue tant que j'ai accumulé moins de 20.

lml-mike · #14

Merci les gars, j'ai trouvé là un merveilleux jeu à boire

rivas · #15

Bonjour Yanneck,

Je vais relire ta démonstration de Q3 en détail pour la comprendre.

On n'a pas la même démonstration mais on arrive au même résultat
On joue jusqu'à avoir 13 points d'avance puis on arrête.

Merci d'avoir pris le temps de rédiger.

dylasse · #16

Pour la question 3, je ne suis pas convaincu par la réponse de Yanneck.

En effet, tu compares les chances de perdre de notre adversaire avec 1/2 pour justifier que tu arrêtes de jouer.
Je pense qu'il faut comparer ces chances non pas avec 1/2 mais avec les chances qu'il a de perdre si tu continues. Ce sont ces dernières qui sont difficiles à formaliser car elles doivent intégrer le fait que si tu continues, tu te reposeras une question à l'issue du tour suivant.

Si mes remarques peuvent faire avancer le schmilblik...

Yannek · #17

Bon remarque Dylasse, c'est vrai que je n'ai donné que la différence de score qui donne une proba d'avoir plus de 50% de chances de gagner en s'arrêtant.

C'est insuffisant pour dégager une stratégie optimale.

Ce qui est (presque) sûr, c'est qu'il ne faut pas continuer au delà : à supposer que l'on puisse jouer au prochain coup (6/36 de perdre, 5/36 de gagner, et 25 /36 de continuer), la situation s'empire en moyenne : la différence de score reste constante en moyenne mais en moyenne la proba de gagner en s'arrêtant baisse (parce que la proba de gagner en s'arrêtant est convexe : plus la différence de score est importante plus elle augmente, mais elle augmente de moins en moins vite).

En revanche on peut considérer l'idée de s'arrêter avant : si on joue sans s'arrêter, le joueur qui commence a 5/11=0,4545... de perdre (c'est un jeu où celui qui est sur le point de lancer le dé est en situation défavorable). On peut alors décider de s'arrêter à une différence de score de 11 et l'on gagne avec une proba de 0,4566. (En comparant le 5/11 à ce résultat, on néglige alors le cas où l'on se fait remonter par l'adversaire et la situation est inversée, le tout sans 1, mais je conjecture que c'est suffisamment rare pour ne pas changer la donne).

Merci pour la remarque, Dylasse.

kosmogol · #18

Bon, ce n'est pas tout ça, moi je vais aller tester cela au bistrot du coin

gelule · #19

Tu bois seul, Kosmo, ou on peut venir avec toi?

kosmogol · #20

viende, au croisement de la rue Bossut et Daumesnil

(et il y a le wifi)

gelule · #21

C'est trop loin, je vais mourir de soif avant d'être arrivé

kosmogol · #22

Amène tes tonneaux !

gelule · #23

Mon grand-père était marchand de vin et nous n'avons conservé que les foudres, je te dis pas le travail

rivas · #24

dylasse a écrit:
Pour la question 3, je ne suis pas convaincu par la réponse de Yanneck.

En effet, tu compares les chances de perdre de notre adversaire avec 1/2 pour justifier que tu arrêtes de jouer.
Je pense qu'il faut comparer ces chances non pas avec 1/2 mais avec les chances qu'il a de perdre si tu continues. Ce sont ces dernières qui sont difficiles à formaliser car elles doivent intégrer le fait que si tu continues, tu te reposeras une question à l'issue du tour suivant.

Si mes remarques peuvent faire avancer le schmilblik...

Je ne suis pas sûr d'être d'accord.
J'ai adopté le même raisonnement que Yanneck pour la raison suivante.
A chaque tour, on doit prendre un décision. La décision se prend uniquement sur les données connues à l'instant 't'. Si à cet instant la probabilité de gagner est >50% on prend la décision d'arrêter. Dans ce cas on considère la probabilité de perdre de l'adversaire ce qui est valide par l'action du Tiers-exclus (pas de match nul).
Evidemment la connaissance du futur modifie la décision mais il n'est pas légitime d'utiliser une connaissance future pour décider. Sinon tous les jeux pour lesquels on essaye de batir une stratégie ne seraient pas possible.

On pourrait en tenir compte mais dans ce cas on travaillerait avec des probabilité conditionnelles p(A)=p(A/B).p(B) et ça reviendrait peut-être au même...

C'est juste mon avis....
Mais je le partage.

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 21-11-2010 17:35:29

Le je du 1

#0 Pub

#2 - 21-11-2010 17:52:11

L jeu du 1

#3 - 22-11-2010 10:47:03

le keu du 1

#4 - 22-11-2010 17:36:11

le keu du 1

#5 - 22-11-2010 21:21:02

le jru du 1

#6 - 23-11-2010 18:30:47

Le eju du 1

#7 - 25-11-2010 06:21:10

le jey du 1

#8 - 25-11-2010 12:05:23

lr jeu du 1

#9 - 25-11-2010 16:28:59

Lee jeu du 1

#10 - 25-11-2010 18:02:15

Le eju du 1

#11 - 27-11-2010 17:38:14

le jeu su 1

Code:

#12 - 27-11-2010 17:41:03

Le jue du 1

#13 - 28-11-2010 13:45:50

eL jeu du 1

#14 - 28-11-2010 15:27:59

Le jjeu du 1

#15 - 29-11-2010 10:00:53

Le eu du 1

#16 - 29-11-2010 16:22:57

Le jjeu du 1

#17 - 29-11-2010 18:13:27

Le jeu d 1

#18 - 29-11-2010 18:19:32

Le jeuu du 1

#19 - 29-11-2010 18:29:37

le jru du 1

#20 - 29-11-2010 18:39:33

Le jeu du

#21 - 29-11-2010 18:49:40

lz jeu du 1

#22 - 29-11-2010 18:52:26

Le jeu u 1

#23 - 29-11-2010 19:02:35

le jeu di 1

#24 - 30-11-2010 14:48:11

lr jeu du 1

dylasse a écrit:

Réponse rapide

Sujets similaires

Mots clés des moteurs de recherche

Pied de page des forums