 |
#1 - 06-12-2010 21:05:40
- silbana
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 2
Passer sur tous les traits sans lever le crayo,n impossible ?
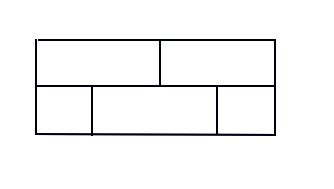
Bonjour, j'aimerai savoir si ce casse tête est possible. Le but est de passer par tous les cotés sans lever son crayon mais on ne peut pas passer 2 fois par le même côté. Voici la figure:
#2 - 06-12-2010 22:13:39
- blaxe
- Habitué de Prise2Tete
- Enigmes résolues : 27
- Messages : 12
Passer sur tous les traits sans lever le crayon, impossible ??
C'est impossible : Car quand tu as un croisement, il faut y arriver et en repartir...
Donc il faut deux "voies" à chaque croisement !
Mais parfois, tu peux arriver au croisement, en repartir, y revenir et repartir. (On voit cet exemple en traçant un 4 par exemple)
Dans ce cas, il y a 4 voies à chaque croisement.
De toute façon, un nombre divisible par deux !
Les deux seuls cas où ce nombre de voies n'est pas divisible par 2 sont le début et la fin, donc tu ne peux avoir plus de 2 croisements avec un nombre impair de voies (Le cas du 4 marche ( 2 croisements à 1voie !) mais pas celui du E (3croisements à 1voie, 1 croisement à 3 voies))
D'ailleurs je pense que cette condition est obligatoire et est la seule condition pour ce genre de problème.
Donc n'importe quel problème du type "tracer sans lever le crayon" n'est faisable qu'avec un nombre quelconque de croisements à un nombre pair de voies et avec au maximum deux croisements à un nombre impair de voies.
#4 - 08-12-2010 15:13:43
- thecourge
- Habitué de Prise2Tete
- Enigmes résolues : 48
- Messages : 31
passer sur tius les traits sans lever le crayon, impossible ?
et si on replie la feuille pour écrire à son verso et replacer son trait où on le désire?
"Chérie! Y'a plus d'papier!!"
#5 - 08-12-2010 15:22:10
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
passer sur tous les trauts sans lever le crayon, impossible ?
Non plus, parce qu'il y a trois points triples à l'intérieur du motif...
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#6 - 08-12-2010 15:43:04
- thecourge
- Habitué de Prise2Tete
- Enigmes résolues : 48
- Messages : 31
Passer sur tous les traits san slever le crayon, impossible ?
on peut plier plusieurs fois de diverses façons...
"Chérie! Y'a plus d'papier!!"
#7 - 08-12-2010 17:00:02
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Passer sur tos les traits sans lever le crayon, impossible ?
Dans ce cas, oui. Si on peut plier la feuille, tout est possible...
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#8 - 08-12-2010 19:02:22
- silbana
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 2
passer sur tous les traits sans lever le crayon, imposdible ?
d'accord, merci pour toutes vos réponses:)
#9 - 18-07-2011 13:39:13
- jazzchris
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 2
Passer sur tous les traits sans leve rle crayon, impossible ?
Bonjour,
Hier, on m'a proposé presque la même énigme. Faire ce même dessin, mais en trois coups de crayon et sans jamais repasser par le même endroit.
Est-ce réalisable, car je m'arrache les cheveux.
D'avance merci pour vos réponses.
JazzCHris
#10 - 18-07-2011 13:42:37
- kosmogol
- Banni
- Enigmes résolues : 49
- Messages : 11,928E+3
Passer sur tosu les traits sans lever le crayon, impossible ?
As-tu le droit de plier le papier (je ne sais pas en quoi cela pourrait aider, mais bon, gardons espoir) ? car sinon il me semble inutile de chercher plus.
http://enigmusique.blogspot.com/
#11 - 18-07-2011 14:11:28
- jazzchris
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 2
Passer sur tous les ttraits sans lever le crayon, impossible ?
Oui, car pas précisé dans l'énoncé que c'est interdit.
Car sinon, c'est une énigme impossible?
#12 - 18-07-2011 14:17:23
- kosmogol
- Banni
- Enigmes résolues : 49
- Messages : 11,928E+3
Passer sur tous les traits sans lever le crayon, ipmossible ?
A mon avis, mais il faut demander aux vrais matheux du site 
http://enigmusique.blogspot.com/
#13 - 18-07-2011 17:04:13
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Passer sur tous les traits sans lever le crayyon, impossible ?
Pour la même raison que Mathias sans plier c'est impossible.
En pliant aussi mais je ne serais pas comment l'expliquer. (D'abord il faudrait que j'en sois sûr.)
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#14 - 18-07-2011 19:49:30
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Passer sur otus les traits sans lever le crayon, impossible ?
En pliant on peut :
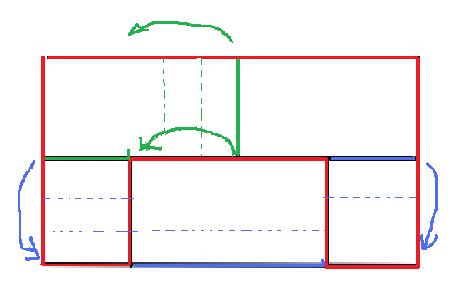
Sans plier ça parait impossible.
#15 - 24-10-2012 12:13:35
Passer sur tous les traits sans lever le rayon, impossible ?
En fait la solution dépend du choix entre 2 hypothèses qui sont à valider une au détriment de l’autre :
1) soit on considère que les intersections de deux arêtes comptent pour un passage dans deux arêtes en même temps.
2) soit on considère que les intersections de deux arêtes sont des points « neutres » et que le passage par ces points d ‘intersection ne compte pas comme passage dans aucune des deux arêtes dont il est justement l’intersection.
l’idée centrale, c’est que l’on est obligé de choisir entre une ou une autre de ces hypothèse, car si l’une est vrai, l’autre est nécessairement fausse et vice versa.
Si l’on opte pour l’hypothèse 1 alors vous trouverez facilement un tracé qui passe essentiellement par des point d’intersection qui valide le passage de 2 au minimum et 3 au maximum arêtes
Si l’on opte pour l’hypothèse numéro 2, alors vous trouverez facilement un tracé qui passe par toutes les arêtes et au moins un point d’intersection.
#16 - 24-10-2012 15:02:03
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
passer sur tous les traitq sans lever le crayon, impossible ?
Heu oui Giancarlo. Moi, j'avais compris que le trait devait passer par toutes les arêtes (et donc aussi par tous les points), ce qui est impossible à réaliser si on n'a pas le droit de passer deux fois par la même arête. A vrai dire, je ne comprends pas ton histoire d'hypothèses exclusives.
#17 - 25-10-2012 15:36:29
Passer usr tous les traits sans lever le crayon, impossible ?
Bonjour Franky
merci d avoir pris le temps de commenter mon message.
je vais essayé de m expliqué plus clairement.
prenons le cas spécifique qu'est le point d intersection de 2 ou 3 arêtes.
ce point peut être considéré uniquement de 2 manières:
1) il fait parti des arêtes
2 il n 'en fait pas parti
si on considère la possibilité numéro 1 , et que ce point intersection fait bien parti des arêtes, on pourra considérer que le passage du trait par ce point d intersection en validera le passage par les arêtes dont il est justement le point d intersection.
Par contre , Si on considère que le passage par une arête ne valide pas le passage du trait par les arêtes dont il est le point intersection, ceci implique nécessairement que ce point est a considérer comme neutre ( puisque il n appartient pas aux arêtes) donc passer par ce point , ne signifie pas passer par les arêtes qui en constitue l intersection
l idée c'est que nécessairement une de ces deux hypothèses doit être validée, car les points d intersection ne peuvent être a la fois perçus comme, faisant parti des arêtes et en même temps , n' en faisant pas parti.
l' énigme est résoluble si on peut montrer qu' independamment du choix de l hypothèse que l'on prendra, il peut être résolu.
si en effet tu prends comme valide l hypothèse numéro 1, tu peux facilement résoudre l énigme en faisant passe ton trait par une majorité de point d'intersection d arêtes.
si tu prends comme valide l hypothèse numéro 2 tu verras que tu pourras faire passer ton trait par toutes les arêtes en passant une fois au moins une fois par un point d intersection considéré comme neutre .
j espère avoir été plus clair dans mon explication.
ciao,
giancarlo
#18 - 25-10-2012 20:20:14
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Passer sur tous les traits sans lever le crayon,, impossible ?
C'est l'hypothèse 1 2, pardon qui me gène, parce qu'on l'a tous prise comme implicite et là, je ne vois pas comment tu trouves "facilement" une solution car je ne pense pas qu'il y en ait.
#19 - 25-10-2012 21:05:41
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
passer sur yous les traits sans lever le crayon, impossible ?
Personnellement, je ne sais pas comment réagir au fait qu'un topic mort et sur lequel tout le monde a conclu "c'est impossible" (c'est d'ailleurs un résultat mathématique très célèbre) est ranimé par quelqu'un qui clame qu'il y a une solution. Et sans nous la montrer, en plus 
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#20 - 25-10-2012 21:27:58
- giancarlo
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 6
Passer su tous les traits sans lever le crayon, impossible ?
on est bien d accord sur le fait que l énoncé de cette "énigme", ne spécifie pas que le trait ne doit pas passer par les points d intersection des arêtes.
donc si le trait peut y passer ceci peux avoir deux conséquences:
soit le passage du trait par les point d intersection compte pour passage des arêtes respective, soit il ne compte pas.
Si il ne compte pas, comme dans mon hypothèse numéro 2, alors il permet a un certain moment de passé par un point d intersection ( neutre ) afin de rejoindre une arête qui serait inatteignable sans passer par une autre arête déjà utilisée.
je me suis permis de vous dessiner 1 solution pour chacune des hypothèses. veuillez trouvez les dessins dans le link suivant.
http://www.prise2tete.fr/upload/giancar … rected.png
#21 - 25-10-2012 23:35:19
- racine
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1224
passer sur tous les traits sans lever ke crayon, impossible ?
Pour moi ça marche, mais je sais pas pourquoi je sens que ça va discuter sec.
#22 - 26-10-2012 00:14:02
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Passer sur tous less traits sans lever le crayon, impossible ?
Plus clair avec l'image. C'est une façon de jouer avec la soi-disant imprécision de l'énoncé, et je ne sais toujours pas si ça m'énerve ou si ça m'amuse. Dans le doute, je vais crier de rire : AHAHAHAHAHAHAHB*RDELHAHAHA  
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#23 - 26-10-2012 00:27:12
- SHTF47
- Imprnnçbl de Prs2Tt
- Enigmes résolues : 39
- Messages : 1629
- Lieu: Autre nom du colin
passrr sur tous les traits sans lever le crayon, impossible ?
La musique est une mathématique sonore, la mathématique une musique silencieuse. [Edouard HERRIOT]
#24 - 26-10-2012 07:03:11
- giancarlo
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 6
passer sur tous les trairs sans lever le crayon, impossible ?
En fait je ne joue pas avec l imprécision de l énoncé, mais simplement avec les propriétés logique implicites de celui ci. Je montre que pour éviter l 'écueil de ce reproche, on peu résoudre le problème des deux manières indépendamment du choix que l on a effectué; simplement cette solution va au bout de la logique de chacun de ces choix opérés et prend en compte l'ensemble des possibilités logiques que permet l énoncé du problème soulevé.
Il y a une réponse effectivement mathématique qui a été apporté a ce problème, mais en réalité, celle ci répond a une autre problème, que certains on voulu appliquer a celui ci, faute de savoir y répondre. Et comme la solution avait une formulation mathématique, elle a convenu a tout le monde.
C'est a mon sens cette solution mathématique,qui est basée sur un changement inacceptable de l' énigme, en arbitrant implicitement que l'on ne pouvait pas passer par les sommets. et pourquoi donc? en voila une prise de position bien aventureuse, au vu et su de ce que contient l’énoncé original!
Il est tout de même curieux, que la solution qui tient compte de toute l'ouverture de l'énoncé et de l ensemble des possibilités qu'elle contient, puisse être suspectée de le modifier en dehors de ces intentions originelles, alors que personne ne s' offusque du fait que la soit disant " solution mathématique généralement acceptée par tous depuis des années, modifie de manière patente, ce même énoncé.
Pour information, la solution mathématique est pertinente uniquement lorsque le problème soulevé est énoncé de la manière suivante ou analogue :
"Si vous avez 5 chambres ( disposée selon le schéma que l'on connait) et que chaque chambre est muni d'une ouverture ( porte) dans chacun des cotés de chaque mur, pouvez vous passer par toutes les "portes " sans passer deux fois par la même porte? "
Dans ce cas précis la réponse mathématique que l'on connait est valable et pertinente . Mais comme vous pouvez le constater on a modifié et restreint de manière substantielle, l'énonce de l' énigme qui nous occupe.
Les raisonnements mathématiques ne sont qu'une forme d'expression et une formalisation de la logique et ne la comprennent pas entièrement , ni bien entendu, peuvent la dépasser. La ou il y a une solution mathématique, il y a toujours a la base, un raisonnement logique, le contraire, n'est pas toujours vrai.
#25 - 26-10-2012 09:44:06
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
Passer sur tous les traits sans lever le crayon, impossibble ?
"Si vous avez 5 chambres ( disposée selon le schéma que l'on connait) et que chaque chambre est muni d'une ouverture ( porte) dans chacun des cotés de chaque mur, pouvez vous passer par toutes les "portes " sans passer deux fois par la même porte? "
Moi, je viens avec une hache et je fais un trou dans le mur, ça compte aussi ?
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum








