Explications :
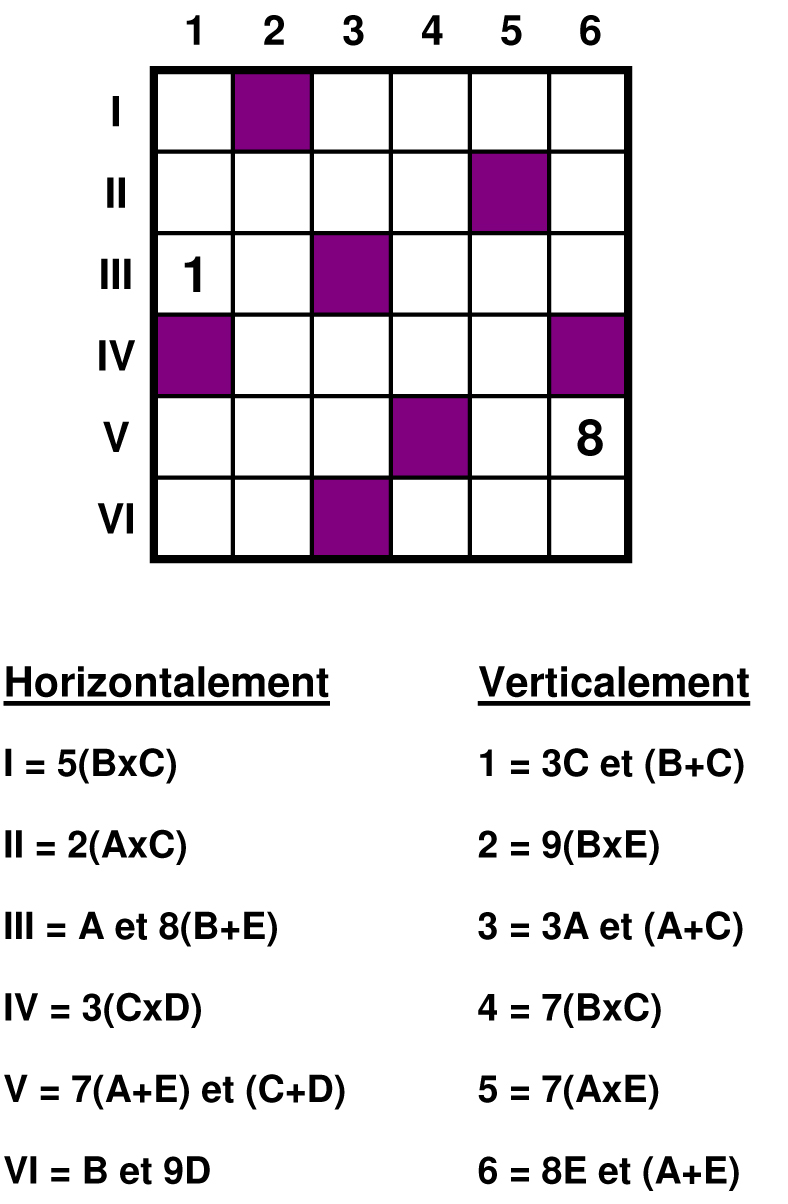
d'après (1), 3C se termine par 1, donc C est de la forme 10x+7
d'après (V), (C+D) se termine par 8, donc D est de la forme 10x+1
on retrouve 9D en (VI), 9D=90x+9, ça se termine forcément par 9.
Donc d'après (6) A+E = 89, il s'ensuit que en (V), 7(A+E) = 623.
D'après (1), on cherche ensuite (B+C)=60+x tel que C se termine par un 7, et que B commence par x. Deux solutions possibles : C=37 et B=25 ou C=47 et B=14.
Or d'après (III) 10<=A<=19, et avec 6 A+E=89, il vient que 70<=E<=79, et en (6) nous avons 8E soit 560<=8E<636. Comme en (I) nous avons 5(BxC), il semble clair que dans la case [I6] nous avons forcément un 5.
Si nouos reprenons nos couples B et C, le premier donne 5x(37x25)=925 et le second 5x(47x14)= 3290, qui ne convient pas.
Il nous reste donc C=37 et B=25.
Nous avons ensuite en (2) 9x(BxE)=xxx25 => E=xxx25/(9x25), avec 70<=E<=79.
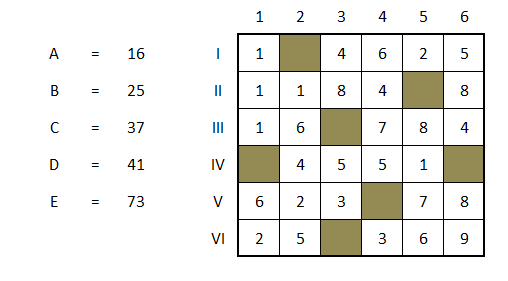
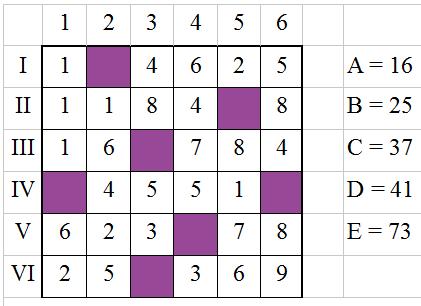
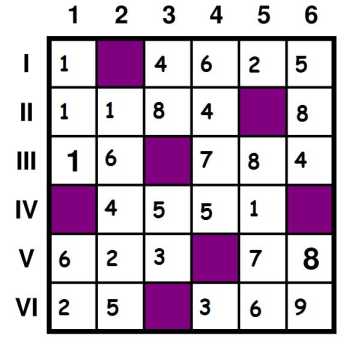
Une seule solution, E=73, donc A=16.
On trouve assez rapidement ensuite D=41 (après avoir rempli la grille ^^).

 Accueil
Accueil
 Forum
Forum