 |
#1 - 09-03-2011 20:56:51
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
Cecle
Quel est le rayon du cercle ci-dessous ?

C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#2 - 09-03-2011 22:00:13
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
ceecle
Prenons C comme origine.
Le point E (0,4∗176)=343 est sur le cercle car CA*CB=CD*CE.
(puissance de C par rapport au cercle).
Le centre est situé à x=17−42=132 et y=34−186=83
La puissance de C par rapport au cercle est −4∗17=d2−R2.
Donc R2=x2+y2+68=(132)2+(83)2+68
R2=1694+649+68=(9∗169+4∗64)9∗4+68=422536R=\sqr422536=656≈10.83333333333
#3 - 09-03-2011 22:06:00
- thedoums
- Professionnel de Prise2Tete
- Enigmes résolues : 23
- Messages : 223
#4 - 09-03-2011 22:09:44
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
Cercl
thedoums, pas loin ! 
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#5 - 09-03-2011 22:21:57
- SHTF47
- Imprnnçbl de Prs2Tt
- Enigmes résolues : 39
- Messages : 1629
- Lieu: Autre nom du colin
cervle
Appelons O le centre du cercle et O' le projeté orthogonal de O sur AB.
Travaillons avec des mesures d'angle en radian.
On peut calculer facilement les angles (AC,AD) et (BC,BD). Ils valent respectivement :
Arctan(3/2) et Arctan(6/17).
On en déduit que l'angle (DA,DB) mesure : π-(Arctan(3/2)+Arctan(6/17))
D'après les relations entre angle au centre et angle inscrit, on en déduit que l'angle ouvert (OA,OB) est tel que: (OA,OB)=2(DA,DB), et que l'angle fermé (OA,OB) vaut donc :
2π-2(DA,DB)=2(Arctan(3/2)+Arctan(6/17))
Comme OA=OB=R (rayon du cercle), OAB est un triangle isocèle en O, et donc:
(AO,AO')+Arctan(3/2)+Arctan(6/17)=π/2
Or (AO,AO')=Arccos(AO'/AO)=Arcos(17/(2R))
D'où: 17/(2R)=cos(π/2-(Arctan(3/2)+Arctan(6/17))=sin(Arctan(3/2)+Arctan(6/17))
Donc : R=17/(2sin(Arctan(3/2)+Arctan(6/17)))
Valeur approchée : R=8.7698
Si c'est le cas, alors le centre du cercle n'est pas très loin au dessus de AB...
La musique est une mathématique sonore, la mathématique une musique silencieuse. [Edouard HERRIOT]
#6 - 09-03-2011 22:22:10
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
Cerle
Soit O le centre du cercle, R le rayon du cercle, H le centre de [AB], E la projection de D sur OH :
R2=OA2=AH2+OH2=10,52+OH2R2=OD2=OE2+DE2=(OH+6)2+6,52
donc :
10,52+OH2=(OH+6)2+6,52
D'où on déduit que :
OH=8/3
Puis :
R=65/6
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#7 - 09-03-2011 22:27:24
- gabrielduflot
- Expert de Prise2Tete
- Enigmes résolues : 34
- Messages : 609
CCercle
on a dans un triangle R=abc\4Soù S est l'aire du triangle
Aire du triangle ABD=21×62=63cm²
on a AD=√52 et BD=√325 et R=21×√52×√3254×63=2730252=10.83
#8 - 09-03-2011 22:30:00
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
Cerlce
Oui, fix et gabriel.
Erreur de calcul pour SHTF47.
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#9 - 09-03-2011 23:15:39
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
ercle
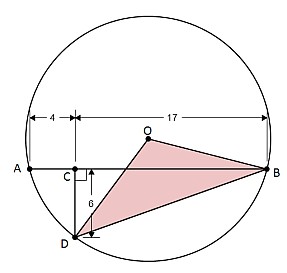
Par Pythagore :
AD=2\sqr13
BD=5\sqr13
sin(DAC)=62\sqr13
Or BOD = 2.DAC (ils interceptent la même corde [BD])
En travaillant dans le triangle rectangle moitié du triangle OBD, on trouve :
OD . sin(BOD/2) = 5\sqr132
OD . 62\sqr13 = 5\sqr132
Donc OD=656
#10 - 09-03-2011 23:19:53
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
Crcle
Très jolie réponse de looozer. 
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#11 - 10-03-2011 00:51:23
- bd-42
- Amateur de Prise2Tete
- Enigmes résolues : 18
- Messages : 2
cetcle
Paramétrons le problème.
Soit le repère (O,x,y) d'origine le centre du cercle et R le rayon de ce dernier.
Avec un peu de geométrie elementaire on a les coordonnées suivantes:
A(-10.5,y(A))
B(10,5,y(B))
C(-6.5,y(C))
D(-6.5,y(D))
On remarque que y(A)=y(B)=y(C)=y(D)+6.
On a donc plus que deux inconnues (R et y(D)<- par exemple). Pour resoudre cela, il nous faut donc deux équations independantes.
On utilise alors l'expression cartesienne du cercle: x²+y²=R². Le fait que les points A et D appartiennent au cercle de nous donne alors le système suivant:
10.5²+(y(D)+6)²=R²
6.5²+y(D)²=R²
Après resolution, on trouve alors environ 10,8cm pour R.
#12 - 10-03-2011 01:52:30
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
cercke
Je note E le point diamétralement opposé à B, et d le diamètre du cercle
Les triangles ABE et BDE sont rectangles en A et D (diamètre=hypothénuse), et BCD est rectangle en C :
AE2+AB2=d2ED2+DB2=d2BD2=CD2+BC2
Pour calculer DE, je me sers de F, projeté de E sur la droite CD, EFD est rectangle en F :
ED2=EF2+FD2FD=FC+CDFC=EA,EF=ACED2=AC2+(AE+CD)2
On obtient donc 2 relations à 2 inconnues AE et d :
AE2+212=d242+(AE+6)2+172+62=d2
On peut en déduire AE par différence des 2 équations :
AE=163
Puis on en déduit d :
d=653
Et enfin le rayon du cercle : R=656
#13 - 10-03-2011 11:51:07
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
Cerce
Bonjour,
Voici ma solution qui est - j'en conviens - un peu "bulldozer".
Soit x0 et y0 les coordonnées du centre du cercle et R son rayon.
L'origine de mon repère sera pris au milieu de A et B.
L'équation du cercle est: (x-x0)^2 + (y-y0)^2 = R^2.
A cause de la symétrie, il est évident que x0 = 0.
Par ailleurs, les coordonnées de A et D sont: A(-10,5;0) et D(-6,5;6).
Ce qui nous donne: 6,5^2 + (y+6)^2 = R^2 et 10,5^2 + y^2 = R^2.
Et on trouve y0=8/3 soit env. 2,667 et R=65/6 soit env. 10,833.
Bonne journée.
Frank
#14 - 10-03-2011 17:09:03
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
Cerrcle
Des as de la géométrie, vous êtes. 
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#15 - 10-03-2011 22:32:28
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
Cecrle
Celui-là est plus simple.
Soit X la distance de l'horizontale au centre du cercle et R le rayon du cercle.
On identifie deux relations pythagoriennes:
R^2=10.5^2+X^2
R^2=(x+6)^2+6.5^2
ce qui donne pratiquement directement
X=8/3 et R=65/6
The proof of the pudding is in the eating.
#16 - 10-03-2011 22:36:07
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
vercle
Oui, sans problème, Franck. Le nouveau problème posté est d'un niveau supérieur. 
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#17 - 11-03-2011 12:51:33
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
eCrcle
Un promath- actif dans un forum actif
#18 - 11-03-2011 23:24:18
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Cerclle
Si on veut faire plus "propre" on multiplie par six les dimensions originales , deux angles inscrits nous donnent deux triangles semblables et on finit avec Pythagore R=65 . On divise par six pour coller avec le problème 

Vasimolo
#19 - 12-03-2011 09:38:31
- dylasse
- Professionnel de Prise2Tete
- Enigmes résolues : 21
- Messages : 378
crrcle
Dans le repère (C,CBx,Cy), nous avons les coordonnées suivantes :
A(-4;0), B(17;0) et D(0;-6).
Le centre O du cercle est sur la médiatrice de AB, donc il a pour coordonnées O(13/2 ; y)
OA²=OD² donc (21/2)²+y² = (13/2)²+(y+6)² qui donne y=8/3
Le rayon cherché est r=OA=racine((21/2)²+(8/3)²)=65/6
Il y a peut-être moins bourrin, mais ça marche !
#20 - 12-03-2011 09:41:12
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
Cercl
Excellent dylasse ! Vasimolo, c'est plutôt astucieux comme démo !
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#21 - 12-03-2011 12:47:47
- debutant1
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 116
ercle
O centre du cercle
tg(adb)= tg(adc+cdb) = (tg(adc)+tg(cdb))/(1-tg(adc)*tg(cdb))
aôb = 2*pi - 2adb (angle au centre)
R * sin (bôh) = r* sin(aôb/2) =21/2=10,5
R = 10,5 / sin (aôb/2) = 10,5 / sin(adb)
tg'adb)= 3,9375
sin(adb)= 0,968
R= 10,85
#22 - 12-03-2011 15:07:46
- mitsuidewi
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 250
- Lieu: dans une chambre universitaire
Cerlce
Eureka !
on calcule en fait le rayon du cercle circonscrit au triangle ABD.
on peut donc écrire la fameuse loi des sinus :
ABsin^ADB=ADsin^ABD=DBsin^DAB=2R
donc
R=\frac{BD}{2sin{\hat{BAD}}
avec :BD=√172+62=√325=5√13
et :sin^BAD=6AD=6√42+62=3√13
On a donc : R=5√1323√13=656
t'en penses quoi SaintPierre ?
#23 - 12-03-2011 15:28:54
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
cerclz
Le rayon est 65/6 = 10.833333333
il suffisait de poser 2 équations.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#24 - 12-03-2011 20:52:45
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
cercme
Un promath- actif dans un forum actif
#25 - 13-03-2011 15:17:07
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
cetcle
Compare ta réponse avec les autres, tu verras bien que oui !
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum









