Bonjour,

1- Une coupe de n'importe quelle partie du circuit perpendiculairement à la trajectoire est un triangle rectangle isocèle dont la base horizontale et le coté vertical font $10\sqrt2$m de coté. L'hypothénuse inclinée de 45° fait elle 20m (largeur de la piste).
La première voiture roule à 5 m du bord bas de la piste et la seconde à 15m du même bord. En considérant les voitures comme des points ponctuels, la voiture du bas effectue dans le virage un arc de cercle horizontal de $40+\dfrac{10\sqrt2}4$ m et la seconde un arc de cercle horizontal de $40+3.\dfrac{10\sqrt2}4$ m. Sur les lignes droites elles effectuent un parcours de même longueur. La différence de marche est donc de: $2\pi.\dfrac{10\sqrt2}2=10\pi\sqrt{2}$, soit environ 44,43m.

2- En supprimant les sections droites pour le moment on obtient une sorte d'arène circulaire. Cette arène est un cyclindre de rayon $R=10\sqrt2$ et de hauteur R évidée d'un cône à 45° dont la pointe est en bas au centre du cylindre. Le cylindre à un volume de $2\pi.R^2.R$ et le cône que l'on lui retire a une volume de $2\pi.R^2.\dfrac{R}3$. L'arène représentant les 2 virages à donc un volume total de: $4\pi\dfrac{R^3}3=\dfrac{8000\pi\sqrt2}3$.
Les sections droites ont un volume de $500\dfrac{R^2}2=50000$.

Le volume total de béton est donc environ: 61848 m3 de béton.


Merci pour cette énigme.
J'espère ne pas m'être trompé. J'ai fait les calculs de 2 façons différentes pour le volume des virages et je n'ai pas trouvé la même chose les 2 fois, j'ai gardé la façon la plus simple

Edit: Quel idiot je suis, si on enlève les parties droites, on n'a pas du tout ce que j'écris ci-dessus. C'est pour cela que je ne trouvais pas les mêmes résultats en appliquant Guldin

1. Il n'y a aucune différence de longueur parcourue sur les lignes droites, on s'intéressera donc uniquement aux parties courbes.

Avec ce schéma:



On a $R_1=40+AD_1\times \cos(45^{\circ})=40+5 \dfrac{\sqrt{2}}{2}$
Et de la même manière $R_2=40+AD_2\times \cos(45^{\circ})=40+15 \dfrac{\sqrt{2}}{2}$

La différence de longueurs sur les deux demi-cercles est donc de:
$$2\pi R_2 - 2\pi R_1=2\pi \left(40+15 \dfrac{\sqrt{2}}{2}-\left(40+5 \dfrac{\sqrt{2}}{2}\right)\right)=2\pi \times 10\dfrac{\sqrt{2}}{2}=10\pi \sqrt{2}\approx 44,43 m$$
2. Pour ce qui est du volume de la piste, avec $\mathcal{A}$ l'aire de la section de la piste (le triangle rectangle isocèle d'hypothénuse $20 m$) qui vaut:
$$\mathcal{A}=\left(\dfrac{20}{\sqrt{2}}\right)^2*\dfrac{1}{2}=100m^2$$
- On a alors le volume pour les deux sections rectilignes qui vaut :
$$2\times \mathcal{l}\times \mathcal{A}=2\times 500\times 100=10^5m^3$$
- On a le volume pour les deux sections circulaires qui vaut, d'après le théorèmes de Guldin:
$$2\pi \times \mathcal{d} \times \mathcal{A}$$
Reste à trouver $\mathcal{d}$, la distance de l'axe de rotation au centre de gravité du triangle.

D'après ce schéma:

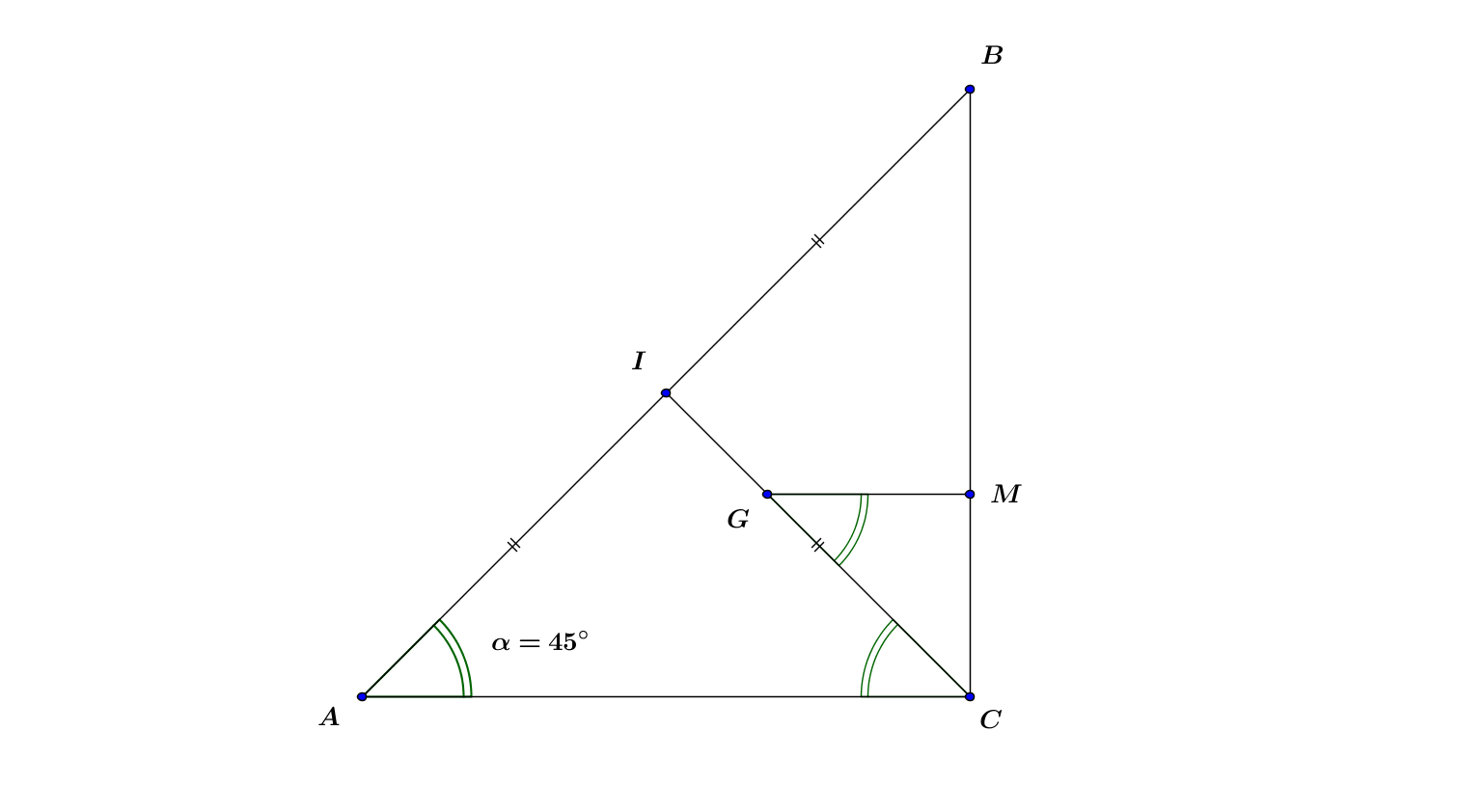
$$\mathcal{d}=40+AC-GM$$
On a $CI=AI=10 \text{ et }CG=\dfrac{2}{3}CI=\dfrac{20}{3}$
Et $GM$ vaut: $\dfrac{20}{3}\times \dfrac{\sqrt{2}}{2}=\dfrac{10\sqrt{2}}{3}$

Ainsi : $\mathcal{d}=40+\dfrac{20\sqrt{2}}{2}-\dfrac{10\sqrt{2}}{3}=10\left(4+\sqrt{2}-\dfrac{\sqrt{2}}{3}\right)=10\left(\dfrac{12+2\sqrt{2}}{3}\right)=20\left(\dfrac{6+\sqrt{2}}{3}\right)$

Et donc:
$$2\pi \times \mathcal{d} \times \mathcal{A}=2\pi \times \dfrac{20}{3}(6+\sqrt{2})\times 100=4000\dfrac{\pi}{3}(6+\sqrt{2})\approx 31\;057m^3$$
Le volume total de béton étant au final:
$$4000\dfrac{\pi}{3}(6+\sqrt{2})+10^5\approx 131\;057m^3$$

1 )

2pi (40 + 15/rac2 ) - 2pi (40 + 5/rac2 )
= 20pi / rac2
=44,428 m

2 ) 10/rac2 pi ( (40+20/rac2)^2 - 40^2 ) + 1000 ( 20^2 /4 )
=  10/rac2  pi ( 1600/rac2 + 200 ) + 100 000
= (8000+1000rac2 ) pi  + 100000
=129575,6 m3

1.
$$R_{ext}=20+15cos(45)$$
$$R_{int}=20+5cos(45)$$
$$avance=2\pi[R_{ext}-R_{int}]=10\pi\sqrt2$$
L'avance de la voiture extérieure est de 44.4m

Edit: R=40 et non 20

2.
L'aire de la piste est un demi-carré de coté $20cos(45)=10\sqrt2$ m
l'aire est 100 m²
Le volume de la partie rectiligne est $\rm 2*500*100=100 000 m^3$
Le centre de gravité du triangle est à 10 m du cote intérieur, le rayon de G est de 30 m.
Le volume de la partie circulaire est $\rm2\pi*aire*R_G=6000\pi\approx18 850 m^3$
Le volume de béton est de 118 850 m³

Edit: R=40 et G est mal placé !

Le calcul de Kikuchi me semble correct et l'explication aussi.
Il donne la même réponse que Frank avec une méthode tout à fait différente.

Looping, ton intégrale n'est pas bonne, ou plus précisemment la formule de la couronne n'est pas bonne par rapport aux bornes entre lesquelles tu intègres.

L'aire d'une couronne est: $\pi((40+10\sqrt2)^2-(40+x)^2)$.
Ou x est la distance au centre de la couche à intégrer.
Il faut donc calculer: $\pi\int_0^{10\sqrt2}(40+10\sqrt2)^2-(40+x)^2dx$

Ce qui donne bien environ 31056 et on retrouve les résultats précédents.

Merci pour l'astuce. En fait c'était un cylindre moins un 'tronc' de cône

Bonjour,
Avez vous remarqué comment on a vite fait de se tromper dans un bête calcul de volume de béton sur un chantier ? Et quand ça arrive, vous avez les oreilles qui sifflent !!!
Bonne journée à tous.
Frank
Edit: A bientôt pour une énigme de mon cru (en cours).

Pas si simple, en effet...



Soit avec R = 40, une avance de 44,4 m et des poussières...

Oh que c'est inutilement compliqué et incorrect.

La réponse de Kikuchi est bien meilleure. C'est le théorème de Guldin qu'il faut utiliser ici.

Tout le raisonnement est correct mais une petite maladresse à la fin, tu écrit :
$$\dfrac{R^2L}{8}+\dfrac{\pi R^3}{48}(\sqrt{2}+6)=\dfrac{R^2}{48}\left[ 8L+\pi R(\sqrt{2}+6) \right]$$
Alors que ça devrait être:
$$\dfrac{R^2L}{8}+\dfrac{\pi R^3}{48}(\sqrt{2}+6)=\dfrac{R^2}{48}\left[ 6L+\pi R(\sqrt{2}+6) \right]$$
Pour arriver au final à:
$$R^2\left(\dfrac{L}{8}+0.485R\right)\approx 131\:040 m^3$$

Ah merci Kikuchi, le 6 au lieu du 8, pfff...