Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 29-07-2011 18:19:17
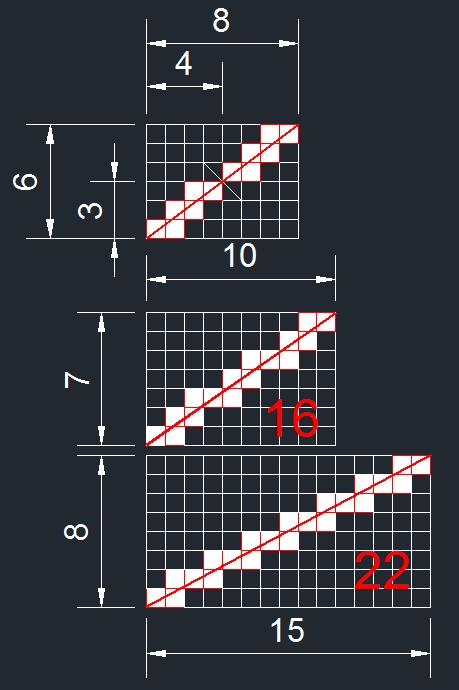
DiagonnaleSoit un rectangle de côtés entiers a et b. On divise ce rectangle en a.b carrés unités. Un mathématicien complet est topologiquement fermé!
#0 Pub#2 - 29-07-2011 19:54:30
Diagonaesoit k le pgcd de a et b The proof of the pudding is in the eating. #3 - 29-07-2011 20:41:05#4 - 30-07-2011 15:07:19#5 - 30-07-2011 15:55:31
diagonakePremière réponse : si a et b sont premiers entre eux, une diagonale ne passera pas par les coins de certains carrés intérieurs. Et comme elle partira d'une case d'un des coins du grand rectangle, et devra "voyager" de a−1 carrés unités dans une direction et b−1 dans une autre. La diagonale traversera donc a+b−1 carrés. Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298 #6 - 30-07-2011 16:17:30#7 - 30-07-2011 19:06:28
DigaonaleBonjour, #8 - 31-07-2011 18:35:14#9 - 01-08-2011 15:51:18
diagobaleSi a et b sont premiers entre eux: #10 - 01-08-2011 17:17:09
siagonalePour commencer la diagonale ne peux pas passer par 4 carrés accolés les uns aux autres ayant en commun un sommet car la diagonale passerai au maximum par trois de ces carrés et non quatre puisque sinon ce serai le sommet. "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline #11 - 01-08-2011 20:23:33Réponse rapideSujets similaires
Mots clés des moteurs de recherche |
 | ||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.