Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 18-09-2011 13:25:29
Masr attaqueBonjour à tous
#0 Pub#2 - 18-09-2011 23:49:23
mzrs attaqueBonjour, #3 - 19-09-2011 13:07:16#4 - 19-09-2011 22:44:29#5 - 20-09-2011 18:08:41
mars atyaqueOn part du principe que les 3 centres ne peuvent pas être alignés puisqu'il sont distinct sur un même cercle ( toujours de même rayon d'ailleurs...) #6 - 20-09-2011 22:43:05#7 - 20-09-2011 23:32:06
Mars attaquBonjour, #8 - 21-09-2011 15:51:18
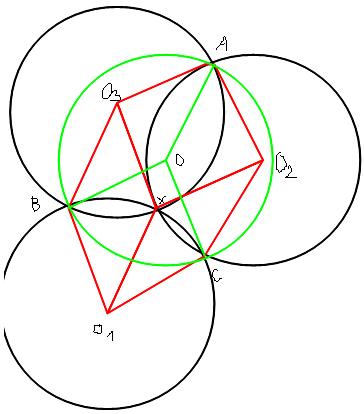
Mars atatqueVoilà comment j'avais vu les choses : #9 - 21-09-2011 18:13:43
Mars attaquBah, je suis content, on a presque le même dessin ! Réponse rapideSujets similaires
Mots clés des moteurs de recherche
|
 | ||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.