Bonjour,
Sous la Chantilly sont cachées les
myrtilles restantes du gâteau 48.
Non, ce n'est pas ça ?
Bonne soirée.
Frank

Je précise que c'est un rond blanc et pas un carré blanc , bref , des yeux chastes peuvent regarder sous le cache

Si , si , je vous connais

Vasimolo

En effet Nodgim , plutôt expéditif

Vasimolo

ça ne doit pas être très simple de fabriquer un irrégulier avec répartition égale des aires de part et d'autre des 3 diagonales....

Je ne comprends pas la question

Bonjour,

On devrait trouver sous la couche de crème que les trois diagonales sont concourantes ....



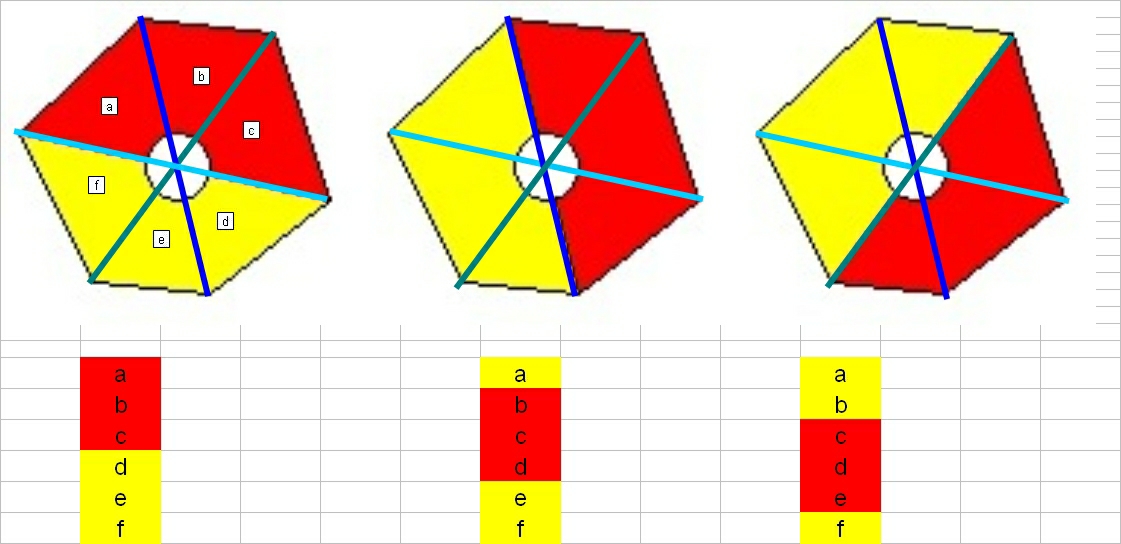
En partant de cette hypothèse,
si l'on nomme, a,b,c,d,e,f les aires des 6 parts triangulaires formées, qui ont donc un sommet commun (l'intersection des diagonales)

alors,
a+b+c = d+e+f
b+c+d = a+e+f
c+d+e = a+b+f

qui conduit à :
a=d
b=e
c=f


J'essaie un raisonnement plus robuste pour prouver la concourance.
Essayons par l'absurde :

Si les diagonales ne sont pas concourantes, alors il y a une surface triangulaire g formée par les trois points d'intersection O O' O"



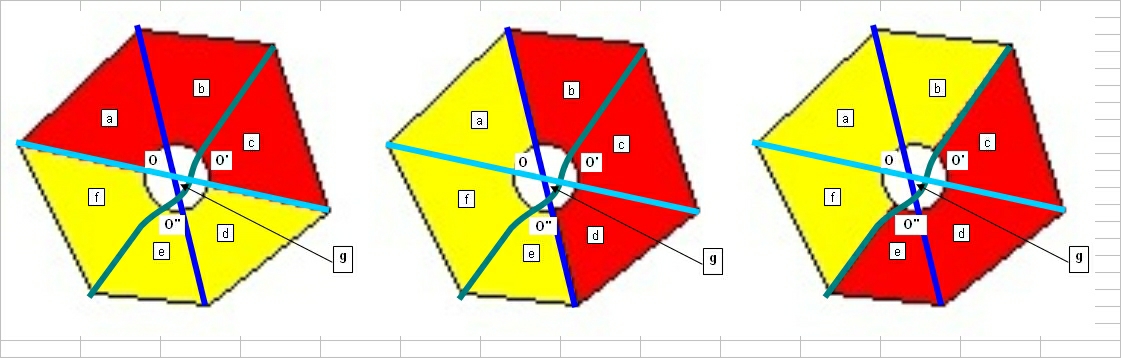
ou, représenté avec déformation de l'hexagone de l'énoncé :




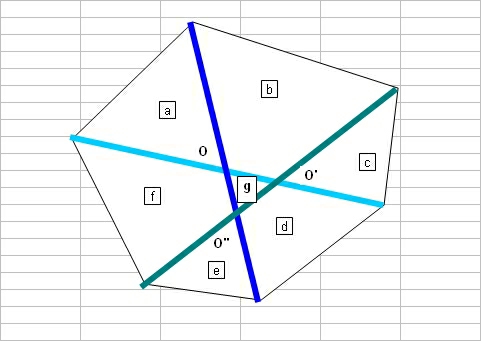
L'égalité des aires donnée dans l'énoncé se traduit alors selon le système suivant :

a+b+c     = d+e+f+g = S/2
b+c+d+g = a+e+f     = S/2
c+d+e     = a+b+f+g = S/2

avec S = a+b+c+d+e+f+g

qui se simplifie en

a = d+g
e = b+g
c  = f+g

Il faut arriver à prouver que g=0, c'est à dire qu'il n'y a donc pas de surface g sous la chantilly.
i.e : les points O, O' et O" sont confondus (en excuses...)
i.e : Les diagonales sont concourantes
i.e : Les parts "diamètralement" opposées sont égales

AAaaaaah !, je suis (merci pour le MP) pensais être arrivé à bout d'un tes gâteaux, moi qui ne suis pas "sucré" !




Merci,
A bientôt,

Ah oui, c'est vrai, il suffit par exemple d'allonger une diagonale également de part et d'autre....

Bonjour Vasimolo,
C'est probablement une question incongrue, mais les six côtés ne semblent pas de longueur égale, ou est-ce la relative petite taille de ton image...?

Comme une grande diagonale coupe le gâteau en deux aires égales, cette droite passe par le centre de gravité du gâteau.
Ceci étant vrai pour les trois grandes diagonales, on en déduit qu'elles sont concourantes au centre de gravité.

Un triangle équilatérale...

Imaginons un triangle au centre du gâteau....
Pour que la découpe partage le gâteau en 2 parts égales à chaque fois, il faut que, en terme de surface :

Z1 + Zx = Z4
Z3 + Zx = Z6
Z5 + Zx = Z2

a,b,c,d,e,f, x1 , x2 et x3 étant les longueurs des côtés indiqués, on a alors :

(a+x1)(b+x3) = ed
(d+x1)(c+x2) = af
(f+x2)(e+x3) = bc

On pose une petite multiplication de tout ce bazar :

(a+x1)(b+x3)(c+x2)(d+x1)(e+x3)(f+x2) = abcdef

Soit x1 = x2 = x3 = 0  Le triangle est réduit à un point.

La pastille cache donc un point de concourance.

La démonstration de loozer est simple et efficace... Bravo ! !