 |
#1 - 23-01-2012 23:57:59
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
visitrz toutes les pièces.
Cette maison possède une unique porte d'entrée qui vous permet d'entrer dans la pièce figurée en marron sur le dessin. Cette pièce vous permet d'accéder à une des 3 pièces voisines et ainsi de suite.
Votre but est de visiter toutes les pièces de la maison sans jamais repasser par une pièce déjà visitée.

#2 - 24-01-2012 00:47:20
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
visitez toytes les pièces.
C'est impossible !
Pour la démo, je pense que le fait qu'on ai une longeur et une largeur impaires et que tu commences sur une case de parité opposé a un coin fait que c'est impossible.
#3 - 24-01-2012 00:51:32
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Visitez toutes le pièces.
#4 - 24-01-2012 08:56:13
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
Visitez toutes les picèes.
Doit-t-on ressortir par la porte d'entrée ? Si oui il faut passer au moins 2 fois dans la pièce située dernière la porte d'entrée.
#5 - 24-01-2012 10:12:09
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Visitez touets les pièces.
Non, on n'est pas obligé.
#6 - 24-01-2012 11:58:29
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1968
visitez toites les pièces.
On colorie cette grille à la manière d'un damier, en considérant que l'entrée est sur une case blanche. Il y a 121 cases; 61 noires et 60 blanches.
A partir d'une blanche, je peux aller sur une noire et vice versa.
Conclusion: en partant d'une blanche, et après avoir visité 120 cases (peu importe comment); j'arrive sur une case noire et la seule case restante à visiter est noire aussi: c'est donc impossible
#7 - 24-01-2012 12:26:56
- ash00
- Sage de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,929E+3
visitez toures les pièces.
Seul Chuck Norris peut y arriver 
#8 - 24-01-2012 17:37:28
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
visitez toures les pièces.
C'est impossible car les dimensions de la grille sont toutes les deux impaires.
Colorions la grille comme un échiquier, et supposons que la case de laquelle on part est noire (donc les coins de la grille sont tous les quatre blancs). On se débarrasse ensuite des cases dans l'ordre : blanc, noir, blanc, etc. Après 118 mouvements, on se retrouve sur une case noire, la soixantième que l'on visite, et on a aussi vu 59 cases blanches. Il nous reste donc deux cases blanches à parcourir, et il est clair qu'on ne peut pas les traverser l'une à la suite de l'autre.
Ce principe de coloriage de grille est un classique, on l'a déjà vu il y a plus de deux ans dans la Balade Royale de Vasimolo (entre autres) qui m'avait rappelé un vieux problème que j'avais posté sous le nom Balade de Tour. (Oui, je fais mon vieux, et alors ?  ) )
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#9 - 24-01-2012 18:11:08
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
visitez toutzs les pièces.
On ne peut pas, y a un nombre impair de cases.
ça me fait penser que j'avais proposé sur un autre site un problème un peu plus compliqué qui est resté sans réponse jusqu'aujourd'hui. Ce serait peut être l'occasion de le ressortir....
#10 - 24-01-2012 18:28:13
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
visitez toutes les piècrs.
On ne peut pas.
Le quadrillage comporte 121 cases.
Si on colorie ces cases comme un damier, il y a 60 cases de la couleur de la case de départ et 61 cases de l'autre couleur.
On change de couleur à chaque déplacement, donc si on veut avoir une chance de pouvoir couvrir toutes les cases, il faut partir et arriver d'une case de la couleur présente sur les 61 cases et non d'une case de la couleur présente sur 60 cases.
Amusant. J'ai un peu cherché avant de vraiment chercher.
Bien dans le style du Ha-ha.
#11 - 24-01-2012 18:29:10
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
VVisitez toutes les pièces.
En coloriant la grille comme un échiquier , ça ne colle pas avec les couleurs 
Vasimolo
#12 - 24-01-2012 19:11:57
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
visitez toutes lrs pièces.
Bonjour,
Cet exercice est impossible à réaliser: voici une démonstration possible.
Colorions les pièces de la maison à l'image d'un échiquier 11 x 11.
Nous aurons 60 pièces kakies et 61 pièces blanches (total: 121 pièces).
On commence par une pièce kakie et on accède à une pièce voisine en changeant de couleur à chaque étape.
Lorsqu'on sera à la 119è piéce, il ne restera plus de pièce kakie, mais seulement deux pièces blanches, forcément non voisines.
Merci pour cette sympathique énigme.
Bonne soirée.
Frank
#13 - 24-01-2012 19:55:44
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
Visitez toutes ls pièces.
J'ai envie de dire que c'est impossible, de même pour tous les carré de côté 4n+3.
Dans tous les autres cas, c'est possible, comme le montre ces exemple avec des carrés de côté 8,9,10
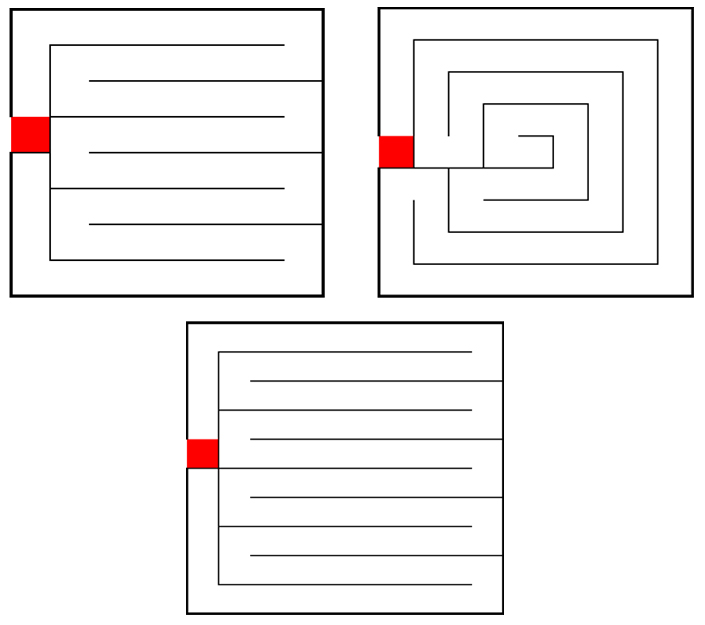
Mais il me reste à montrer que c'est impossible pour le dernier cas, ou alors à trouver une solution !!!
#14 - 24-01-2012 21:13:25
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
Visitez toutes les ipèces.
Voici une jolie nouvelle version du problème des sept ponts de Königsberg dont la démonstration ne me parait pas aussi évidente que celle réalisée par Euler en son temps : il n'y a bien sûr aucune solution à ce problème  ! !
#15 - 25-01-2012 17:39:32
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
viqitez toutes les pièces.
Il n'est pas possible de visiter toutes les pièces de la maison sans jamais repasser par une pièce déjà visitée.
En effet colorons les pièces en noir ou en blanc comme au jeu de dames.
Convenons que la pièce où l'on entre est noire.
Supposons qu'une telle visite soit possible.
Alors on doit visiter 61 pièces blanches et 60 pièces noires.
Les pièces noires et blanches alternent le long du parcours de la visite.
Par suite la 1ère et la dernière pièce visitées doivent être blanches.
Or la 1ère pièce est noire (entrée), d'où contradiction.
#16 - 26-01-2012 13:46:33
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Visitez toues les pièces.
pour un carre de taille imparire (11x11) il n'est pas possible de commencer ou finir sur une piece de coordonnees de type different (paire,impair) comme (0,5), il faut commencer et finir sur des coordonnes de meme type (pair, pair) ou (impair,impair),
sinon au mieux on ne peut pas acceder a une des pieces.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#17 - 26-01-2012 18:16:24
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
visitez toutes les pièxes.
Bravo à tous ceux qui ont trouvé le pourquoi du comment.
Effectivement, si l'on colorie les pièces comme les cases d'un damier, avec des pièces blanches dans les coins, on voit qu'il n'est pas possible de passer par toutes les pièces de la maison une fois et une seule si l'on commence par une pièce noire.
Une condition nécessaire pour que l'on puisse trouver un parcours adéquat est que la pièce désignée pour le départ (et/ou la pièce désignée pour l'arrivée) soit une pièce blanche.
Réciproquement, si je vous désigne une pièce blanche de départ et une pièce blanche d'arrivée, sera-t-il toujours possible de les relier en passant par toutes les autres pièces de la maison une fois et une seule ?
#18 - 28-01-2012 01:16:01
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
visirez toutes les pièces.
J'ai compris pourquoi avec un carré de 9x9 j'y arrivais ... La case au milieu d'un côté du carré est de la même couleur que celle des coins  En changeant de couleur de case de départ, par contre, on arrive bien aussi à une impossibilité. En changeant de couleur de case de départ, par contre, on arrive bien aussi à une impossibilité.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum







