 |
#26 - 04-02-2012 19:20:58
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,431E+3
Visitez toutes les pèces. Le retour.
#27 - 05-02-2012 02:19:23
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
visutez toutes les pièces. le retour.
Merci pour l'illustration !
Tiens, pour le c, il y aurait pas un problème pour la méthode exposée dans le cas suivant ?
XXXXX
XNNNX
XNNNX
XNNDX
XXXXD
#28 - 05-02-2012 10:16:04
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Visite toutes les pièces. Le retour.
La récurrence est elle aussi démontrée pour un rectangle impair*impair ?
#29 - 05-02-2012 11:28:07
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,431E+3
Visitez toutse les pièces. Le retour.
titoufred a écrit:Tiens, pour le c, il y aurait pas un problème pour la méthode exposée dans le cas suivant ?
XXXXX
XNNNX
XNNNX
XNNDX
XXXXD
Il y a en effet un problème , il semble impossible dans cette situation de raccorder un chemin à l'intérieur du carré central à un parcours sur la couronne extérieure .
On peut quand même s'en sortir en considérant un carré NXN coincé dans l'angle opposé aux deux cases incriminées .
Je vais essayer d'illustrer ça 
Vasimolo
#30 - 05-02-2012 11:56:38
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,431E+3
Visitez toutes ls pièces. Le retour.
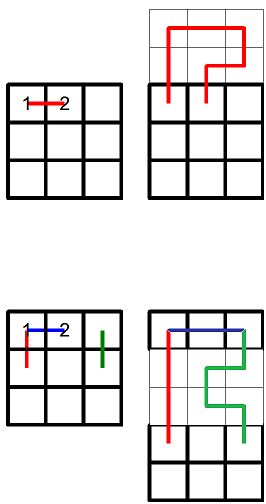
Voilà 

En ajoutant toutes les vaguelettes nécessaires pour atteindre le coin en bas à gauche du carré vert .
Vasimolo
#31 - 05-02-2012 12:00:16
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3223
- Lieu: Luxembourg
visitez toutes les pièces. le retoue.
@Vasimolo
Merci pour tes schémas illustrant la récurrence et surtout d'avoir "sauvé" cette solution qui commencait à avoir du plomb dans l'aile
@nodgim
Si je pars sur un rectangle de 3 x K (K impair et supérieur à 3), j'arrive à démontrer que ça marche pour tout rectangle (3+2N)x(K+2N), donc finalement pour tout rectangle impair x impair
#32 - 05-02-2012 12:08:31
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,431E+3
Visitez toutes les pièces. Le reetour.
nodgim a écrit:La récurrence est elle aussi démontrée pour un rectangle impair*impair ?
J'ai un contre-exemple avec un rectangle 1X5 
Vasimolo
#33 - 05-02-2012 15:26:10
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Visitez totues les pièces. Le retour.
Vasimolo a écrit:Voilà 

En ajoutant toutes les vaguelettes nécessaires pour atteindre le coin en bas à gauche du carré vert .
Vasimolo
Bien joué !
#34 - 05-02-2012 15:29:18
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Visitez tooutes les pièces. Le retour.
Franky1103 a écrit:@nodgim
Si je pars sur un rectangle de 3 x K (K impair et supérieur à 3), j'arrive à démontrer que ça marche pour tout rectangle (3+2N)x(K+2N), donc finalement pour tout rectangle impair x impair
Oui, le résultat doit s'étendre de la même façon à tous les rectangles de dimensions impaires >=3.
Il reste juste à montrer que ça marche sur les rectangles 3 x K.
#35 - 05-02-2012 16:42:44
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,021E+3
visitez toutes les pièces. lr retour.
Quoiqu'il en soit on passera toujours de la case 1 à la case 2 (idem pour les autres qui sont voisines) . Donc il parait facile de de passer d'un rectangle impair à un autre de largeur ou de longueur +2
#36 - 05-02-2012 17:17:11
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Visitez totues les pièces. Le retour.
Je n'ai pas compris Gwen.
Les extrémités du chemin sont imposées, on est d'accord ?
#37 - 05-02-2012 17:36:06
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,021E+3
visitez toutes les pièceq. le retour.
Oui donc si on choisit deux cases quelles qu'elles soient, on peut toujours ramener ç au problème avec 2 lignes de moins... Il suffit de choisir où on met les deux lignes en rab et de constater qu'elles ne changent rien au parcours.
J'ai juste négligé le cas où on considère les deux lignes en rab une en haut et l'autre en bas...  Mais le principe est le même. Le passage de 3x à 5x5 est particulier ... Mais au delà, il est toujours possible d'exclure deux ligne du problème et de le ramener au cas (-2 lignes) ou (-2 colonnes) Mais le principe est le même. Le passage de 3x à 5x5 est particulier ... Mais au delà, il est toujours possible d'exclure deux ligne du problème et de le ramener au cas (-2 lignes) ou (-2 colonnes)
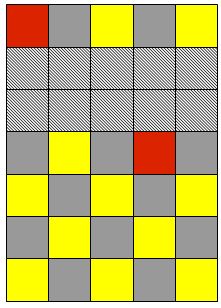
En oubliant les lignes 2 et 3, puis 5 et 6 , puis les colonnes 2 et 3 on en revient au cas 3x3.
#38 - 05-02-2012 17:41:12
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,431E+3
visitez toutes led pièces. le retour.
En tout cas il est facile de vérifier par récurrence qu'en ajoutant un rectangle 3X2 à un rectangle 3XN , toutes les liaisons blanches-blanches restent possibles .
Vasimolo
#39 - 05-02-2012 18:35:44
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,431E+3
visitez toutes les pièceq. le retour.
#40 - 05-02-2012 20:59:01
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
visitez toutes les pièces. ke retour.
Ok Vasimolo, bien vu. Ceci prouve donc que le résultat est valable sur tout rectangle de dimensions impaires >=3.
#41 - 06-02-2012 18:20:03
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Visitez totues les pièces. Le retour.
J'avais posé cette question sur le rectancle impair*impair car la démo que j'ai présentée (quelque peu tombée dans l'oubli..) le prouve de fait.
#42 - 07-02-2012 11:54:41
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,431E+3
Visitez toutess les pièces. Le retour.
Je viens enfin de comprendre ta démo Nodgim ( quelques illustrations m'auraient épargné un terrible mal de tête ) 
Il me semble quand même qu'il y a un problème quand l'un des points est sur le bord supérieur ou inférieur de l'échiquier .
Vasimolo
#43 - 07-02-2012 18:20:52
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
visutez toutes les pièces. le retour.
C'est tout à ton honneur, Vasimomo, d'avoir tenté de comprendre ma démo, elle est simple en fait mais assez longue à expliquer.
Pour le cas particulier de la ligne unique, dans le cas d'un pion en haut ou en bas, j'ai bien envie de proposer dans ce cas là la rotation d'un quart de tour de l'échiquier dès le début de la démo. Qu'en penses tu ?
#44 - 07-02-2012 19:08:30
- racine
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1224
Visitez toutes les pièces. Le retur.
#45 - 07-02-2012 19:11:00
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,431E+3
Visitez toutes les pièces. Le rteour.
Ne nous plaignons pas ça aurait pu être Vasilomo 
Vasimolo
#46 - 07-02-2012 20:29:50
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Visitez toutes les pièces. Le retur.
C'est tout à fait involontaire et ça m'a fait bien rire.
Du sketch: Vas y momo, fais toucher les fils et on démarre (la visite de Paris)
#47 - 07-02-2012 21:19:29
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3223
- Lieu: Luxembourg
Visitez toutes les pièces. Le retour..
Bonjour,
La démonstration de nodgim me semble très astucieuse.
Dans le cas où un des 2 pions est situé sur le bord inférieur ou supérieur, on pourrait effectivement tourner l'échiquier d'un quart de tour. Si le problème persiste (ce qui signifie que ce pion est dans un angle de l'échiquier), alors on se contentera d'un découpage en 3 rectangles (au lieu de 5). Une autre solution consisterait à "forcer" la dimension minimale d'un rectangle à 3 unités.
De même si les 2 pions sont situés sur des cases voisines (en diagonale), alors on ferait un découpage en 4 rectangles (le n°5 serait "dégénéré").
Une soucis survient peut-être quand on a le cas de figure émanant de titoufred, qui avait d'ailleurs déjà mis la récurrence en difficulté:
XXXXX
XXXXX
XXXXX
XXXDX
XXXXD
Bonne soirée.
Frank
#48 - 07-02-2012 23:16:09
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,431E+3
Visitez toutes les pièces. Le retuor.
En fait il y a problème dès que l'une des cases est sur un bord supérieur ou inférieur et que l'autre est dans la même colonne . On doit pouvoir traiter ces cas particulier à part ( sûrement pas par une rotation car la solution de Nodgim suppose que les les cases extrêmes ne sont pas à la même hauteur ) . Va-t-on aboutir à une solution plus simple qu'avec la récurrence , je commence à en douter sérieusement 
Vasimolo
#49 - 08-02-2012 19:13:28
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Visitez toutes les pièces. Le retour
Franky1103 a écrit:XXXXX
XXXXX
XXXXX
XXXDX
XXXXD
Dans ce cas particulier, où même la rotation ne résout pas le problème: Le D dans l'angle est envoyé à gauche (balaye donc le rect 1*5) et celui au dessus remonte tout en haut en balayant les colonnes 4 et 5. Reste alors un rectangle tjs i*p résolvable.
J'ai fait dans ma démo des déplacements tjs identiques pour simplifier, mais du coup pour des cas particuliers comme celui ci je suis obligé de faire autrement. Je vais réfléchir à une stratégie plus générale qui prendra en compte tous les cas de figure. ça risque d'être plus abstrait....
#50 - 09-02-2012 10:51:11
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
visitzz toutes les pièces. le retour.
Je pense que pour un rectangle qui a une dimension paire, on peut toujours trouver un chemin joignant 2 cases données de couleurs différentes.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum















