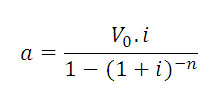Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 07-02-2012 22:12:57
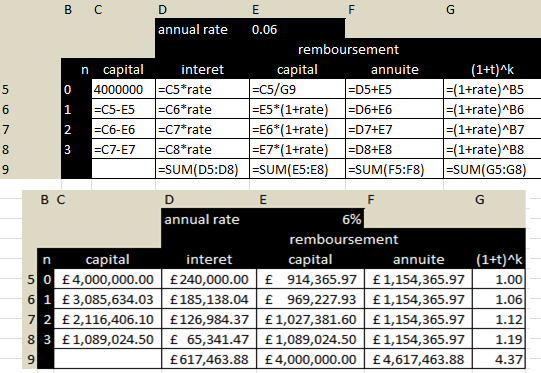
Aidez les bnquiers ... !Un client contracte un emprunt d'un principal de 4 000 000 euros d'après une banque pour un taux de 6% à rembourser pour 4 ans à annuités constantes (ce que paie le client en fin de chaque année. "Zero is where everything starts ! Nothing would ever be born if we didn't depart from there"
#0 Pub#2 - 07-02-2012 23:38:02
Aidez les baanquiers ... !Bonjour, #3 - 08-02-2012 06:01:46#4 - 08-02-2012 10:11:22
Aidez les banquies ... !T'as un DM de maths pour vendredi ? Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298 #5 - 08-02-2012 12:59:39
Aidez les banquiesr ... !bonne réponse de franky et algao "Zero is where everything starts ! Nothing would ever be born if we didn't depart from there" #6 - 08-02-2012 18:39:57
Aidez es banquiers ... !
The proof of the pudding is in the eating. #7 - 09-02-2012 03:23:18
aidez kes banquiers ... !Il y a plusieurs facons de resoudre ce probleme: Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt #8 - 09-02-2012 17:29:20
aidez les bznquiers ... !franck9525 et dhrm77 : Bonne réponse "Zero is where everything starts ! Nothing would ever be born if we didn't depart from there" #9 - 09-02-2012 17:36:23
Aide les banquiers ... !Annuité=P(t+\frac 1 {\sum_{k=0}^{n-1}(1+t)^k}) The proof of the pudding is in the eating. #10 - 10-02-2012 16:46:01
Aidez les banquiers .. .!A une date donnée, il reste X à rembourser. #11 - 10-02-2012 18:05:44#12 - 12-02-2012 11:02:30
aidez les banquierd ... !pour l'enigme de la culture generale celles ou il faut completer les chiffre avec les letre genre 7 a la m = 7 a la maison ou 42 et le R de la vie et le r etc... #13 - 12-02-2012 14:11:45
aidez led banquiers ... !@mustak95: Si tu as un problème avec les énigmes officielles, Rends toi sur le cercle des sages "Zero is where everything starts ! Nothing would ever be born if we didn't depart from there" #14 - 12-02-2012 20:42:46#15 - 13-02-2012 01:20:09
Aidez les banquiers .. !C'est faux graouilly "Zero is where everything starts ! Nothing would ever be born if we didn't depart from there" Réponse rapideSujets similaires
Mots clés des moteurs de recherche |
 | ||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.