Enigme Concours Griego 5&6 @ Prise2Tete

Promath- · #1

J'annonce le concours Griego ouvert!
Il y a 2 parties dans la section mathématiques et 1 partie dans la section logique.
Il y a 2 questions par parties, car vous devez au moins répondre à 4 questions pour faire parti du concours.
Vous indiquerez vos réponses sous forme claire, sans mélanger les 2 problèmes.

1-Les faces d’un pavé droit on des aires de 32 cm², 18 cm² et 4cm².
Quel est le volume du pavé ?

2-Sur les 8 plateaux de ce système, on a placé des poids de 1 à 8 KGs. Le système gravite en équilibre, et le centre de gravité se trouve au milieu.
Replacez les 8 poids.
Si vous pensez que c'est impossible, écrivez 0.

halloduda · #2

1
48

Si les arêtes sont a, b, c, on connaît les produits deux à deux.
Le volume est [latex]abc=\sqrt{ab.bc.ac}=\sqrt{32.18.4}=48\,cm^3[/latex]

2
0

Il n'existe pas de solution.
Si le cercle des centres a pour rayon [latex]\sqrt2[/latex],
l'égalité des moments par rapport à un diamètre s'écrit :
[TeX]a+b\sqrt2=c+d\sqrt2[/TeX]
Impossible avec a, b, c, d entiers et b≠d.

shadock · #3

Exercice 5 :

Ca nous fait un pavé de côté x, y et z que l'on cherche pour trouver sont volume.
On a donc (j'ajouterai une figure si tu veux) un système linéaire de trois équations à deux inconnues telles que :
[TeX]x*y=32[/TeX]
[TeX]y*z=4[/TeX]
[TeX]z*x=18[/TeX]
On abouti à plus ou moins [latex]x=12[/latex] [latex]y=\frac{8}{3}[/latex] et [latex]z=\frac{3}{2}[/latex].

Le volume du pavé est donc [latex]V_{pavé}=xyz=48 \text{ } cm^3[/latex]

Jackv · #4

1 - le volume est égal à la racine carrée du produit des aires, soit 48 cm3.
On peut en déduire les 3 dimensions en divisant cette valeur par chacune des surfaces.

2 - Pour qu'il y ait équilibre selon n'importe quel axe passant par le centre du système il faut et il suffit qu'il y ait équilibre par rapport à 2 axes non confondus, par exemple un axe horizontal et un axe vertical.
On suppose (ce qui n'est pas clairement dit) que tous les plateaux sont à une distance r identique du point "d'articulation" O, de longueur unité, et que les angles entre chacun des plateaux sont tous égaux.
On appelle a, b, ..., h les masses sur les plateaux en partant de l'axe des x >0 et en tournant dans le sens trigonométrique.

L'équation d'équilibre autour de l'axe horizontal s'écrit :
[TeX](c-g) + \sqrt 2 /2* (b+d-f-h) = 0[/TeX]
ce revient à écrire : [latex]2*n = m \sqrt 2[/latex] avec n et m entiers.

C'est rigoureusement impossible. Ce qui était possible avec une "balance" à 6 bras, ne l'est pas avec une "balance" à 8 bras !

Azdod · #5

1- avec un simple système on conclut que les dimensions de ce pavé sont : 12 , 8/3 , 3/2. (cm bien-sur )
[TeX]V=48 cm^3[/TeX]

gilles355 · #6

Exo 1: (Niveau 3ème)

Soit x,y,z les arêtes du pavé droit. On a donc le systeme :

1. xy= 32
2. xz = 4
3. yz = 18

si on divise la premiere et seconde equation on obtient:

1/2. xy/xz = y/z = 32/4 = 8 donc y=8z que l'on remplace dans l'équation 3.

On obtient donc 8z²= 18 d'où z²=18/8=9/4 d'où z=3/2 car longueur positive.
En remplaçant le z dans l'équation 2 on trouve x=8/3.
En remplaçant le x dans l'équation 1 on trouve y= 12.

Le volume du pavé étant xyz, le volume vaut 3/2*8/3*12 = 48 cm cube

Exo 2:

http://www.prise2tete.fr/upload/gilles355-EXO22.jpg

Soit a=OA, b=OB, ... h=OH
On peut considérer que la balance est un repère de centre O et que les poids de 1kg à 8kg sont des vecteurs de longueurs 1 à 8.

a,b,c,...,h étant les valeurs de 1 à 8, on cherche à déterminer qui vaut quoi si c'est possible.

Projection orthogonale sur les axes horizontaux et verticaux des vecteurs OB, OD, OF et OH.

On a donc sur l'axe vertical, vect(OA)+vec(OB2)+vect(OH2)-vect(OD2)-vect(OF2)-vect(OE)=vect(0)

Puisque les angles sont de 45° entre chaque barre de la balance on a donc l'équation :
a+(racine de 2)/2*b+(racine de 2)/2*h-(racine de 2)/2*d-(racine de 2)/2*f-e=0

c'est à dire :
(a-e)+(racine de 2)/2*(b+h-d-f)=0

Dans ce cas là, puisque a,b,c,...,h sont des entiers naturels compris entre 1 et 8, il faut que b+h-d-f=0 et donc que a-e=0 mais alors on doit avoir a=e ce qui est impossible puisque a et e doivent être différent.

Le problème n'a donc pas de solution entières tel que a à h soient tous différents.

MacArony · #7

1 )

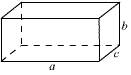
cb = 4
ac = 18
ab = 32

(1) 9/2 (cb) = ac <-> 9/2b = a <-> 9/2b² = 32 <-> b = 8/3
(2) 8/3a = 32 <-> a = 12
(3) 12c = 18 <-> c = 3/2

On obtient donc un Volume = abc = 48 cm³

2) Je n'ai pas compris l'énoncé...
Que veut-dire gravite dans ce cas-ci ? s'agit-il d'une vue du haut ou de face ?

Mac

Grizix · #8

1 - Trivialement, les trois dimensions du pavé sont différentes. Soient A, B, C ces longueurs (non nulles) telles que A>B>C. On a AB>AC>BC.
Donc AB = 32, AC = 18 et BC = 4. Système de trois équations à trois inconnues.
A = 32/B = 18/C <=> B = 32C/18 = 16C/9 = 4²C/3²
BC = (4C/3)² = 2²
C étant positif, on trouve :
C = 3/2cm
B = 8/3cm
A = 12cm

Vérification :
12*8/3 = 32
12*3/2 = 18
8/3*3/2 = 4

2 - Mmh, je vois que les barycentres pour faire ça, ça me saoule, ça doit être impossible
0

emerald000 · #9

1- 48 cm³

2- 0 (Voir explication + contournements de règles)

Je premièrement pensé à mettre les poids 1, 2, 7 et 8 sur le plateau du haut et les poids 3, 4, 5 et 6 sur le plateau du bas.

Si on veut qu'il y ait un et un seul poids sur chacun des plateaux, alors je mettrais un 8 sur le plateau du haut et du bas et un 1 sur les autres plateaux.

Si on veut que les poids soient de 1, 2, 3, 4, 5, 6, 7 et 8 kg et qu'il n'y ait qu'un et un seul poids par plateau et que la masse des poids soit parfaitement répartie sur les plateaux, le problème est impossible à résoudre: (Les variables réfèrent aux points cardinaux.)

Selon l'axe de symétrie horizontale:
o/2 + no + n + ne + e/2 = o/2 + so + s + se + e/2 =>
no + n + ne = so + s + se

Selon l'axe de symétrie passant entre o et no, et e et se:
no + n + ne + e = o + so + s + se

En soustrayant la première équation de la deuxième:
e = o

Contradiction! Les poids doivent être de différentes masses. On ne peut donc pas résoudre le problème avec ses critères.

golgot59 · #10

Le premier problème est simple : on pose que les arêtes ont pour côtés x, y et z cm
alors xy=4
xz=18
yz=32

On cherche xyz, donc il suffit de faire le produit des trois lignes et on obtient :
(xyz)²=4*18*32=2304

donc V=racine(2304)=48 cm^3

pour le second problème :

-----c-----
--d-----b--
e---------a
--f-----h--
-----g-----

Si on calcule les coordonnées du barycentre, il faut commencer par donner les coordonnées des 8 points. Je prend un repère centré sur le point milieu dont le rayon du centre au plateau mesure 1.
Alors les points ont pour coordonnées :
A(1,0) poids a
B(√2,√2) poids b
C(0,1) poids c
D(-√2,√2) poids d
E(-1,0) poids e
F(-√2,-√2) poids f
G(0,-1) poids g
H(√2,-√2) poids h

L'abscisse moyenne est :
x=a*1+b√2+c*0+d*(-√2)+e*(-1)+f*(-√2)+g*0+h*√2=(a-e)+(b-d-f+h)√2

Comme √2 n'est pas un multiple d'un nombre entier, il faut a-e=0 et (b-d-f+h)=0

donc a=e, ce qui est impossible.

Ma réponse est donc 0

(Si on avait eu les plateaux placés sur les bissectrices du repère au milieu des plateaux cardinaux (et pas sur un cercle), alors peut-être eut-ce été possible...)

Promath- · #11

MAC :Il s'agit d'une vue de haut.

N'oubliez pas de répondre aux deux questions!

fred101274 · #12

Pour le 1, en appelant a, b et c les 3 longueurs, il vient ab = 4, ac = 18 et bc = 32, ce qui donne a=3/2, b=8/3 et c=12.

Pour le 2, je vais répondre 0 sans preuve mais pour l'instant, je ne vois aucune solution. (Mais j'ai quand même l'impression qu'il doit en exister une...)

DeepSpeedou2.5 · #13

On note :
a la longueur
b la largeur
c la profondeur

a, b et c vérifient
a * b = 4
a * c = 18
b * c = 32

a = 4/b et c = 32/b donc 32b²-72=0 d'où b=3/2
De plus, a=8/3 et c=12

Le volume du pavé est donc de 48cm^3

Pour la deuxième, si on fait avec les barycentres, il me semble que c'est impossible mais je cherche toujours

L00ping007 · #14

Question 1

En appelant a,b,c les longueurs des 3 côtés, les 3 aires sont ab,ac,bc.
Et le produit de ces 3 aires vaut abacbc=(abc)^2, soit le volume au carré.
Le volume vaut donc la racine de carrée de 32*18*4=2304
Le volume est 48cm3

Question 2

Pour moi, ce n'est pas possible.
Je numérote les masses de 1 à 8 dans le sens des aiguilles d'une montre.
Les 4 plateaux 1,2,3,4 sont du même côté, leur poids doit être identique aux 4 autres 5,6,7,8, soit 18 kg (les 8 masses pèsent 36kgs).
Mais les plateaux 2,3,4,5 doivent aussi peser 18kgs, donc par différence les plateaux 1 et 5 ont la même masse, ce qui est contraire à l'énoncé.
C'est donc impossible

masab · #15

Griego 5
Le volume V du pavé est donné par V=48.

On note a,b,c les côtés du pavé, de sorte que
ab=32
ac=18
bc=4

Alors en divisant les 2 premières équations on a b/c =16/9
Comme bc=4 on a b^2=64/9 d'où b=8/3
On en déduit a=12, c=3/2
D'où le volume du pavé
V = abc = 48
V = 48

Griego 6
Je suppose que tous les poids placés sont distincts deux à deux.
Réponse : 0

Autrement dit il n'y a pas de solution.
Pour le voir on peut noter [latex]a = e^{\mathrm{i} \pi/4}[/latex].
On considère une permutation [latex](n_1,...,n_8)[/latex] de [latex](1,...,8)[/latex].
On considère la somme [latex]\sum_{k=1}^8\ n_k\,a^k[/latex] .
Ces sommes ne sont jamais nulles, ce qui montre qu'il n'y a pas de solution.

Prouvons que ces sommes ne sont pas nulles.
Leur partie réelle est égale à
[TeX]n_8-n_4+(n_1-n_3-n_5+n_7)\frac{\sqrt{2}}{2}[/TeX]
Or [latex]n_1,\cdots,n_8\in\mathbb {N}[/latex], [latex]n_4\not=n_8[/latex] et de plus le nombre [latex]\sqrt{2}[/latex] est irrationnel.
Il en résulte que la partie réelle étudiée n'est pas nulle, donc
[TeX]\sum_{k=1}^8\ n_k\,a^k\not=0[/TeX]

Franky1103 · #16

Re-bonjour,

Partie 5
On aura: ab = 32; bc = 18 et ac = 4; ce qui donne:
c = 4/a; puis b = 4,5.a et enfin 4,5.a² = 32; d'où:
a = 8/3 cm; b = 12 cm et c = 3/2 cm.
Le volume du pavé vaut donc: V = 48 cm³

Partie 6
Si j'appelle les poids successivement dans le sens trigo
a, b, c, d, e, f, g et h, on devra avoir (entre autres):
a + b + c + d = e + f + g + h et b + c + d + e = f + g + h + a
ce qui donne, en soustrayant: a - e = e - a et donc a = e.
Les poids ne peuvent pas être tous différents.
La solution est donc impossible: 0

Re-bonne soirée.

FRiZMOUT · #17

1.

Soient [latex]a[/latex], [latex]b[/latex] et [latex]c[/latex] les dimensions du pavé droit tels que [latex]ab=32[/latex], [latex]ac=18[/latex] et [latex]bc=4[/latex].

On a [latex]ab \times ac \times bc = (abc)² = 32 \times 18 \times 4 = 2304[/latex].
[TeX]V = abc = \sqrt{2304} = 48[/latex].

Le volume du pavé droit est de 48 cm³.

2.

Je dis surement une grosse connerie, mais pour moi, avec des poids successifs [latex]a[/latex], [latex]b[/latex], [latex]c[/latex], [latex]d[/latex], [latex]e[/latex], [latex]f[/latex], [latex]g[/latex] et [latex]h[/latex], l'équilibre est respecté si :

[latex]a+\sqrt{2} \times b+c=e+\sqrt{2} \times f+g[/TeX]
[TeX]b+\sqrt{2} \times c+d=f+\sqrt{2} \times g+h[/TeX]
[TeX]c+\sqrt{2} \times d+e=g+\sqrt{2} \times h+a[/TeX]
[TeX]d+\sqrt{2} \times e+f=h+\sqrt{2} \times a+b[/TeX]
Au vu de l'énoncé, je pense donc que c'est impossible. 0.

Je me permets tout de même de donner une configuration très proche de l'équilibre (si je ne dis pas n'importe quoi, encore une fois) :

Code:

looozer · #18

1.
ab=32 ; bc=18 ; ac=4
On résout le système : a=8/3 ; b=12 ; c=3/2 donc abc=48 (cm³)

2.

Promath- · #19

Loozer:tu n'as pas répondu à la 2?!

Grizix · #20

Oups, je viens de voir que moi j'ai donné les longueurs des côtés pour la 1., mais que j'ai oublié de calculer le volume !

Promath- · #21

Désolé...Mais tu auras un avantage en cas d'égalité de points.

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 24-02-2012 15:00:55

Concours Griego 5&66

#0 Pub

#2 - 24-02-2012 16:04:05

Concours GGriego 5&6

#3 - 24-02-2012 16:09:06

cpncours griego 5&6

#4 - 24-02-2012 16:20:51

Concours Griiego 5&6

#5 - 24-02-2012 19:16:49

cpncours griego 5&6

#6 - 24-02-2012 20:30:34

Concours Griego 5&&6

#7 - 24-02-2012 21:29:14

Concours GGriego 5&6

#8 - 25-02-2012 01:50:30

Concours rGiego 5&6

#9 - 25-02-2012 04:01:54

Concors Griego 5&6

#10 - 25-02-2012 09:25:17

Concours Griego 5&

#11 - 25-02-2012 10:11:04

Concours rGiego 5&6

#12 - 25-02-2012 15:08:09

Concours Griego 5&ammp;6

#13 - 25-02-2012 16:02:51

concours griegi 5&6

#14 - 25-02-2012 16:57:18

Conours Griego 5&6

#15 - 25-02-2012 19:05:08

Concours Griego 5&am;p6

#16 - 25-02-2012 19:50:43

Cncours Griego 5&6

#17 - 25-02-2012 19:58:34

Concours Grigeo 5&6

Code:

#18 - 25-02-2012 22:03:23

concpurs griego 5&6

#19 - 26-02-2012 09:58:26

Concours Griego 5a∓6

#20 - 27-02-2012 17:57:55

Concours Grieggo 5&6

#21 - 28-02-2012 17:44:02

voncours griego 5&6

Réponse rapide

Sujets similaires

Mots clés des moteurs de recherche

Pied de page des forums