Tu parles des noeuds traversés par la boucle ou cernés par la boucle ?

Vasimolo

Ah oui, je comprends mieux, je me suis efforcé de lui faire faire le tour complet de tous les noeuds, mais l'énoncé ne l'exige pas....

C'est, ramené en entiers, le théorème de Green ou Green-Riemann.

http://fr.wikipedia.org/wiki/Th%C3%A9or … e_de_Green

Une démo complète:
Dans une colonne, une ou plusieurs cases à l'intérieur de la boucle, limitée en haut et en bas par le trajet de la boucle: le sens du trajet en haut est opposé au sens en bas: Dans le cas contraire il est impossible de relier les flêches en boucle sans couper l'espace entre les 2 flêches.
Même raisonnemment pour les cases extérieures à la boucle, limitées en haut et en bas par le trajet.
Pour 2 colonnes adjacentes, les 2 limites supérieures de chacune d'elle sont de même sens: Dans l'autre cas, si l'on tente de raccorder les flêches en boucle, on serait obligé de passer au dessus de l'une des flêches.
Ainsi, sur toute l'étendue du domaine entouré par la boucle:

Toutes les flêches supérieures sont de même sens, les flêches inférieures aussi, dans le sens contraire.

Maintenant prenons le cas d'une flêche supérieure sur la ligne 7 et l'inférieure sur la ligne 3: Celle du haut incrémente de +7, et celle du bas décrémente de +3: on a donc bien une différence qui compte le nombre de cases insérées.

Une flêche supérieure en -3, l'autre en -5: résultat +2.

Donc le mode de comptage correspond exactement au nombre de cases entourées par la boucle.

Oui, mais il faut avant tout être certain de l'invariant du sens des flêches !
Ce qui n'est pas une évidence pour les configurations compliquées.

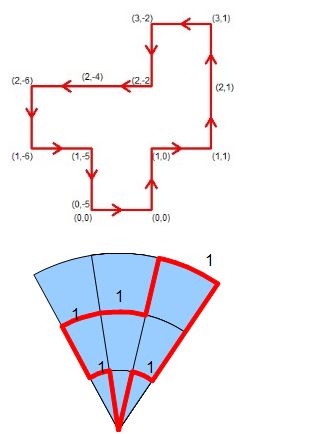
Ca vaut ce que ça vaut, je voyais le problème ramené à des déplacements "unitaires"

Oui, mais ça m'a juste permis de visualiser le problème en oubliant tes compteurs...

Le compteur étant juste le rayon, par colonne on entre et sort de la courbe :
Colonne 1  : 2-1
colonne 2 : 2-0
colonne 3 : 3-1

Le signe donne juste le sens de rotation.

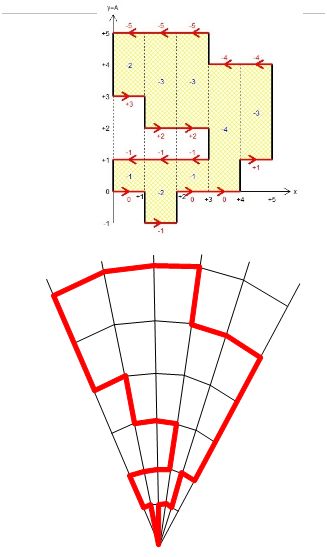
Dans le second exemple :
6-4+2-1
6-3+2
6-3+2-1
5-1
5-2

J'ai d'autant mieux compris que j'avais pensé la même chose

Sur mon dessin il est clair que dans une colonne donnée les flèches alternent leurs directions j'attendais simplement quelque chose de plus propre que : "il est évident ... "

D'un autre côté ces petits problèmes à l'air de rien côtoient de très près des problèmes assez fins d'analyse comme le signalait Halloduda . On peut penser à Green-Riemann mais aussi à Brouwer ou Jordan ... Ici on doit jouer sur le côté borné et orienté de la trajectoire et il n'est pas évident qu'il existe une explication simple qui évite l'artillerie lourde ou le traditionnel : "comme ça se voit sur le dessin" .

Vasimolo

Sinon, une corollaire au problème initial:
On veut que le robot passe par tous les noeuds du carré (1 seule fois) avant de revenir à sa position initiale. J'avais émis cette hypothèse:

Le nombre de cases prisonnières à l'intérieur de la boucle est de n-1 pour un carré comprenant 2n*2n noeuds.

Reste juste à le démontrer.

@Nodgim

Je ne cherche pas à utiliser de gros résultats , au contraire je cherche à les éviter

Quand tu dis que sur la figure suivante on ne peut pas relier continûment les deux flèches sans passer à l'intérieur du carré tu utilises le théorème du point fixe de Brouwer ou un résultat sur les chemins de Jordan .



Évidemment c'est très facile de dire qu'il est clair que le chemin doit traverser le carré . Le problème est du même type que celui des trois maisons à raccorder aux compteurs . Si la réponse doit être : "c'est non parce que ça ce voit !" , où est l'intérêt ?

Vu que le problème est essentiellement discret je me demandais s'il existait une solution faisant l'économie des ces résultats un peu pointus .

Vasimolo

Vasimolo a écrit:

@Nodgim

Je ne cherche pas à utiliser de gros résultats , au contraire je cherche à les éviter

Quand tu dis que sur la figure suivante on ne peut pas relier continûment les deux flèches sans passer à l'intérieur du carré tu utilises le théorème du point fixe de Brouwer ou un résultat sur les chemins de Jordan .

http://img528.imageshack.us/img528/2227/problme.jpg

Évidemment c'est très facile de dire qu'il est clair que le chemin doit traverser le carré . Le problème est du même type que celui des trois maisons à raccorder aux compteurs . Si la réponse doit être : "c'est non parce que ça ce voit !" , où est l'intérêt ?

Vu que le problème est essentiellement discret je me demandais s'il existait une solution faisant l'économie des ces résultats un peu pointus .

Vasimolo

D'accord Vasimolo. Je pensais juste que "l'évidence" que tu mentionnais se rapportait à la boucle complète du dessin, et non aux figures élémentaires. Voilà l'ambiguïté levée.
Maintenant, ce n'est pas tout à fait du visuel, mais de la logique qui se sert du visuel. De la topo de base.
Vas donc tenter de donner la définition d'une droite. C'est un axiome de géométrie.
Si je dessine une boucle, je partage le plan en 2 zones: celle à l'intérieur de la boucle, et celle à l'extérieur. Je considère ça comme un axiome.

Bien sûr que l'on accepte le théorème de Jordan et que l'on est obligé d'y recourir. Sans cela, on ne peut parler de la surface à l'intérieur de la boucle et donc on ne peut pas répondre à l'énigme.

Pour ce qui est de l'alternance du sens des flèches je vois ça comme ça : lorsqu'on parcourt le circuit, l'intérieur se trouve d'un côté, toujours le même, disons à gauche. Maintenant, sur une colonne donnée et de bas en haut : sous la première flèche, on se trouve à l'extérieur de la boucle, donc cette première flèche est vers la droite, donc entre la première et la deuxième flèche on se trouve à l'intérieur, donc la deuxième flèche est vers la gauche, etc...

Peut être oui...Mais alors pourquoi admet-on si facilement l'axiome d'une droite, qui n'est que visuel après tout, et pas celui d'une boucle qui partage le plan en 2 régions ?