C'est la même énigme qu'ici et j'ai la flemme de tout rédiger.

Pour les amateurs:
Et si le loup court 4.6 fois plus vite?

Je pense que si on avance un peu et que le loup s'engage sur un chemin (gauche ou droite), en obliquant de quelques degrés,  on a une distance très peu supérieure à accomplir pour une distance bien supérieure pour le loup.

(bien que je ne sache pas calculer le "point de non retour" , ni l'angle, je pense que c'est jouable)

Il doit même y avoir une courbe qui optimise ce truc... Mais laquelle ?

Il va falloir dériver une fonction trigonométrique en face d'une fonction linéaire pour y arriver ?

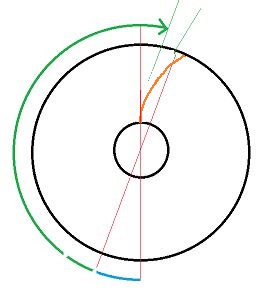
Je me dis que, même si je ne nage pas très vite, je sais observer et me décider rapidement. La portion bleue de mon parcours sur le dessin de gwen27 tend donc vers zéro et je vais directement en ligne droite du petit cercle vers le grand cercle.

Soient k le rapport des vitesses, r le rayon du petit cercle, R celui du grand et A l’angle supplémentaire (exprimé en radians) qu’on souhaite faire parcourir au loup.

r = k.R (avec 0<k<1)
Coordonnées de mon point de départ: (0 ; k.R)
Coordonnées de mon point d’arrivée: (R.sinA ; R.cosA)
Distance que je parcours: d1 = R.[sin²A+(cosA-k)²]^0,5 = R.(k²+1-2k.cosA)^0,5
Distance que parcourt le loup: d2 = R.(pi+A)

On doit avoir: k.d2 > d1
=> k.R.(pi+A) > R.(k²+1-2k.cosA)^0,5
=> k².(pi+A)² > k²+1-2k.cosA
=> k².[(pi+A)²-1]+2k.cosA-1 > 0

Cherchons où: k².[(pi+A)²-1]+2k.cosA-1 s’annule car cela semble correspondre à un optimum et à exprimer k en fonction de A.
k².[(pi+A)²-1]+2k.cosA-1 = 0, avec D/4 = cos²A+[(pi+A)²-1]
=> k = [(D/4)^0,5-cosA]/[(pi+A)²-1], en ne gardant que la racine positive

Et là, même avec l’aide d’un tableur, je cale. J’ai du faire une erreur de raisonnement et/ou de calcul quelquepart. Je reviendrai plus tard.

Avec un seul changement de direction :

(k-(1+x)cos(x))^2 +((1+x)sin(x))^2=pi^2; x<k-1

K étant le rapport des vitesses et x la distance parcourue par le canard en bleu.
Le petit cercle est ramené à un rayon 1... Je trouve un kmax= 4,383 pour x=0,39

EDIT, on doit pouvoir améliorer, si k = pi + 1 + n
On avance de n, puis on dévie vers un angle n (opposé au loup ) et quand il est aligné avec nous, on pique un sprint droit vers le bord. (dessin 1 )

On a gagné le n de distance qui manquait sauf si kn donne trop d'avance au loup (dessin 2)

Ca me dépasse...

Mais bon, mon raisonnement suffit-il à prouver que k=1 + pi n'est pas la limite ?

Du coup je balance l'optimum histoire de garder une trace:
Si v est le rapport des vitesses (ie la vitesse du nageur est de 1 et v est la vitesse du loup) alors on commence comme prévu par tourner sur le petit cercle de rayon R/v avec le loup synchronisé à l’opposé puis on part, non pas radialement jusqu'au bord, mais tangentiellement au cercle et en ligne droite.
Ça peut sembler contre intuitif dans la mesure ou on a envie de dire "mais du coup le loup va partir du coté qui vient à notre encontre" mais en fait c'est le contraire, ce n'est pas le loup qui choisit mais nous:
Supposons qu'on quitte le cercle radialement sur une très petite distance epsilon, (à ce stade le loup a déjà du choisir et a déjà commencé à prendre de l'avance angulairement) puis qu'on tourne d'un certain angle pour aller en ligne droite jusqu'au bord en prenant le coté que le loup n'a pas choisit. Ce dernier n'aura pas intérêt à changer de sens car maintenant en dehors du cercle limite il nous rattrape angulairement. Si jamais il change de sens ça ne peut que nous aider à atteindre une position plus éloignée du centre que R/v ou on l'a dans notre dos.
Dans le raisonnement précédent epsilon peut être aussi petit qu'on le désire et il ne reste que le "certain angle" à déterminer.
Les calculs donnent 90 degrés (on part tangentiellement au cercle R/v) et v limite = 4.6033 et des miettes (limite à laquelle le loup et le nageur suivant ce protocole arrivent en même temps)
Voila voila

Hello,
1) Il se met à nager en rond sur le cercle de rayon R/v et se débrouille pour avoir le loup à l'opposé de lui. (ie aligner lui-même->le centre de la piscine->et le loup dans cet ordre) Il peut le faire parce que jusqu’à ce cercle il a une vitesse angulaire plus grande que celle du loup.
2) Il part ensuite tout droit jusqu'au bord tangentiellement à ce cercle intermédiaire.
Pour les remarques voir mon post précédent.

C'est une remarque que j'ai traitée à l'avance dans le post d'avant à partir de

Ça peut sembler contre intuitif dans la mesure ou...

Et pour y répondre il faut comprendre la suite ou je parle de epsilon.

La stratégie exhibée ci dessus est la stratégie limite, tu peux considérer que la vraie stratégie fait intervenir le segment epsilon et qu'on peut choisir epsilon aussi petit qu'on veut. Ce qui ramène le calcul de la limite à la stratégie décrite.

Mais c'est bien la stratégie du nageur que je décris, qu'est ce qui n'est pas clair? :p
Je refais la stratégie-epsilon avec des steps pour voir ou il y a quiproquo:
1) Nous nageur nous positionnons sur le cercle de rayon R/v avec le loup a l'opposé (on aligne nous->le centre->le loup)
2) On avance radialement (c'est a dire en suivant un des rayon du bassin) d'une distance epsilon vers l'extérieur.
2b) A la fin de ce segment epsilon le loup qui fait les choses bien a déjà du choisir un coté au hasard (puisqu'on ne l'aide pas à choisir) et a commencé à prendre angulairement de l'avance de ce coté la. Avance qu'il ne perdra plus jamais car en dehors de notre petit cercle R/v il va angulairement plus vite que nous quelque soit notre trajectoire.
3) On tourne de 90degres par rapport à notre segment epsilon, en allant du coté que le loup n'a pas choisi et on ira tout droit jusqu'au bord du lac.

NB: De 3 jusqu’à la fin le loup n'a pas d’intérêt à changer de sens car il est en avance angulairement et à chaque instant on se rapproche du bord de la piscine, s'il changeait de sens pendant cette étape alors arriverait de nouveau l'alignement (nous->le centre->le loup) mais cette fois ci encore plus loin du centre du lac que R/v (il suffirait de recommencer 2 dans une position strictement avantageuse pour le nageur)

4) Le segment epsilon en 2) peut être aussi petit qu'on le désire, le comportement limite (avec epsilon tendant vers 0) est une sortie tangentielle au cercle de rayon R/v.

Voila voila. c'est ou que c'est pas clair? je peux le faire avec une fourmi qui court sur un gâteau circulaire si tu veux :p