|
#1 - 09-08-2013 15:43:11
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Est c vrai?
J'ai lu ceci dans un review scientifique américain. Il parait que moins d'1% des diplômés américains en maths, ingénierie et en informatique sont capables de trouver la réponse en moins d'une heure sans utiliser un logiciel graphique. Vérifions. Combien de temps allons-nous mettre en France? J'ai mis moins d'1min et vous? 
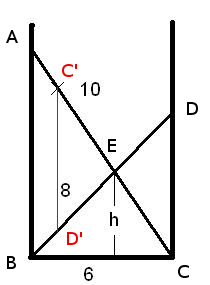
Voici le sujet en image. Deux barres de longueurs 10 m et 8 m sont posées entre 2 mûrs parallèles distantes de 6 m. Trouvez la hauteur h du point de croisement entre les 2 barres.

Réponse à valider avec 5 chiffres après la virgule; le point est utilisé comme séparateur décimal.
La forme réelle du résultat est requise dans les réponses 
Merci pour votre participation
#2 - 09-08-2013 17:10:36
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
est xe vrai?
C'est plutôt simple.
Soit x la distance du point au bord gauche.
On a les égalités : h8=6−x6 et h2√7=x6
D'où par addition l'élimination de x et le résultat :
h=8√74+√7=32√7−569≈3.18489355...m
#3 - 09-08-2013 18:20:41
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Ets ce vrai?
Avec Pythagore, on trouve les hauteurs auxquelles culminent les deux barres : on trouve 8 et √28.
On note x et y les distances du croisement des barres à chacun des deux murs.
D'après Thalès : h8=yx+y et h√28=xx+y
En ajoutant ces deux égalités, on trouve h8+h√28=1
donc
h=118+1√28
#4 - 09-08-2013 18:24:00
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
esr ce vrai?
Que bonnes réponses 
Oui halloduda, c'est plutôt simple je trouve aussi.
#5 - 09-08-2013 18:37:21
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Est ce vraii?
h=32√7−569
Juste un peu de Pythagore et de triangles semblables .
Il n'y a rien de déshonorant d'y passer une petite heure ou plus 
Vasimolo
#6 - 09-08-2013 19:09:09
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
est ce crai?
Equation de la courte échelle: y = x.V7/3
Equation de la longue échelle: y = 8-4.x/3
A l'intersection: x0 = 24/(4+V7) = 8.(4-V7)/3
Et donc: h = y0 = 8.(-7+4V7)/9 = env. 3,18489
Mais il m'a fallu plus d'une minute.
#7 - 09-08-2013 19:26:59
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
esy ce vrai?
Début 19:20
On calcule d'abord les hauteur sur les deux mur par Pythagore :
L=√(10²-6²)=8
l=√(8²-6²)=√28=2√7
Ensuite on utilise la trigo :
α est l'angle en bas à gauche entre la barre et le sol
β le même à droite
Tanα=2√7/6=h/d1 donc d1=3h/√7
Tanβ=8/6=h/d2 donc d2=3h/4
et d1+d2=6
donc h(3/√7+3/4)=6
h=6/(3/√7+3/4)
h=3.18489355
Il est 19:31, 11 minutes en comptant la rédaction.
#8 - 09-08-2013 20:02:25
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Est cce vrai?
ça doit faire quelque chose comme 8rac7/(rac7+4)
En 1 mn, c'est très bien. Il m'a tout de même fallu refaire le dessin et poser l'équation. En principe, accessible aux 1ères, voire secondes.
Après coup, je me suis souvenu que dans ce problème, l'inverse de la hauteur du croisement est égale à la somme des inverses des hauteurs des hauts des 2 échelles (8 et 2rac7 ici).
#9 - 09-08-2013 20:06:02
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Est ce vrrai?
Maintenant, je suis assez surpris que les matheux américains aient échoué là dessus. Je doute de la véracité du renseignement.
#10 - 09-08-2013 21:15:19
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
est cz vrai?
Il y a sûrement plus simple.
#11 - 09-08-2013 22:31:55
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
est ce crai?
Un élève de quatrième peut le faire...
En utilisant Thalès uniquement on trouve le système suivant :
\frac{x}{6}=\frac{h}{2\sqrt{7}}
\frac{6-x}{6}=\frac{h}{8}
On en déduit h=8-\frac{32\sqrt{7}}{7+4\sqrt{7}}=3.18489...
Shadock 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#12 - 09-08-2013 22:50:52
- elpafio
- Elite de Prise2Tete
- Enigmes résolues : 43
- Messages : 1017
Est ce vvrai?
Deux équations du second degré:
y = x * \sqrt 28 / 6
y = (6 - x) * 8 / 6x * \sqrt 28 / 6 = (6 - x) * 8 / 6x * \sqrt 28 / 6 = 8 - ( 8 x / 6 ) x * \sqrt 28 = 48 - 8 x (8 + \sqrt 28) x = 48 x = 48 / (8 + \sqrt 28) y = ( 48 / (8 + \sqrt 28) ) * \sqrt 28 / 6 y = ( 8 * \sqrt 28 ) / (8 + \sqrt 28) y = 3.184893550...
On peut certainement faire plus clair, mais c'est vendredi soir ... 
#13 - 10-08-2013 12:20:07
- gabrielduflot
- Expert de Prise2Tete
- Enigmes résolues : 34
- Messages : 609
esy ce vrai?
On utilise le théorème de Thalès et le théorème de Pythagore
on a h/rac(10²-6²) = a/6 et h/sqrt (8² - 6²) = (6-a)/6
d'où a= 6h/8
donc h/rac 28 = 1 - h/8
enfin h ( 8 + rac 28)/8 rac28 = 1
donc h = 8 rac 28/(8+rac 28)
#14 - 10-08-2013 15:21:43
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
#15 - 10-08-2013 16:28:25
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Esst ce vrai?
Pythagore nous donne le segment de gauche 8 et le segment de droite 2 \sqrt{7}
Le segment de longueur h détermine sur les triangles 6-8-10 et 6- 2 \sqrt{7}-10 deux plus petits triangles semblables aux deux grands.
Si j'appelle x la partie droite de la base (déterminée par le segment de longueur h), j'obtiens deux égalités de rapports de similitudes :
\frac{8}{h}=\frac{6}{x}[/latex] et [latex]\frac{2 \sqrt{7}}{h}=\frac{6}{6-x}
En éliminant x de ces deux équations, on obtient h=\frac{8 \sqrt{7}}{4+\sqrt{7}}
A mon avis, on est plus fort de ce côté-ci de l'Atlantique 
#16 - 10-08-2013 18:37:21
- Autleaf
- Passionné de Prise2Tete
- Enigmes résolues : 48
- Messages : 71
- Lieu: Toulouse
Es ce vrai?
Allons-y alors pour voir si on fait mieux que les américains.
Besoin de rajouter quelques noms sur le dessin histoire de simplifier la lecture des calculs.
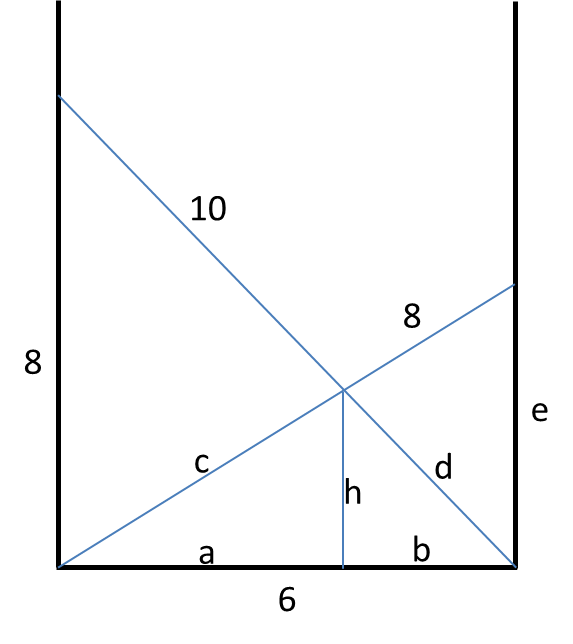
On calcule e facilement avec Pythagore : e=2*rac(7)
Ensuite, Thalès nous permet d'exprimer c et d en fonction de h :
c=8*h/e ; d=10*h/8
Et encore Pythagore pour calculer a et b :
a=rac(c²-h²) ; b=rac(d²-h²)
On finit avec a+b=6 et on remplace tout :
h=6 / [rac(8²/e² -1)+rac(10²/8² -1)]
Et hop : h=3.18489355
Validé par la case réponse ! 
L'honneur est sauf...
#17 - 10-08-2013 19:04:30
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Est ce vra?i
Que de bonnes réponses avec une belle variété de méthodes 
Bravo à tous.
#18 - 10-08-2013 21:27:01
- vladimir37
- Expert de Prise2Tete
- Enigmes résolues : 30
- Messages : 503
- Lieu: nantes
Esst ce vrai?
Soient D la taille du montant de droite et G la taille du montant de gauche.
D'après le théorème du Pythagore,on a les expressions suivantes:
D²+6²=8²[/latex] et [latex]G²+6²=10²
Donc, on a:
D=2\sqrt7
et G=8
Soient d la longueur de la partie située à droite du "croisement" et g la a longueur de la partie située à gauche du "croisement".
Donc on a: g+d=6
D'après le théorème de Thalès, on a les relations suivantes:
g/6=h/D
et
d/6=h/G
Donc on a:
h/D+h/G=1
D'où:
h=(DG)/(D+G)
Soit h=(16\sqrt7)/(8+2\sqrt7)
ou approximativement:
h=3.18489
#19 - 10-08-2013 22:59:30
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
est cz vrai?
Je ne sais pas où je fais une erreur : je ne valide pas.
Ce qui me console que je fais partie de la majorité écrasante 
La barre de 10 m touche le mur de gauche à 8 m de haut (Pythagore).
La barre de 8 m touche l'autre mur à sqrt(28) m de haut (re-Pythagore).
Et par Thales on a (avec x la distance au mur de droite du point d'intersection des barres) :
h/sqrt(28) = (6-x)/6 = 1- x/6
h/8 = x/6
D'où on trouve :
h = 8*sqrt(28)/(8+sqrt(28)) = 8*sqrt(7)/(4+sqrt(7))
soit approximativement 3,18489...
"le point est utilisé comme séparateur décimal" !
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#20 - 11-08-2013 12:53:24
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Est c vrai?
@fix33 : tu as la bonne réponse, la case réponse ne valide pas parce que tu utilises la virgule comme séparateur décimal au lieu du point. Mets ta réponse sous forme "X.Y" où Y est la partie décimale 
#21 - 11-08-2013 19:07:33
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
Est ce vrai
5 bonnes minutes pour une méthode qui je pense est loin d'être la plus rapide 
hauteur du premier triangle => Pythagore => 8m
hauteur du deuxième triangle => Pythagore => 2v7
Pour la première barre : f(x) = -4/3 x + 8
Pour la deuxième barre : f(x) = (v7/3) x
Calcul de x pour le point de croisement
-4/3 x + 8 = (v7/3) x
x = 24 / (v7 + 4)
donc h = (v7/3) * (24 / (v7 + 4))
calculatrice windows 
h = 3,1848935504518776551168560129396
#22 - 12-08-2013 13:20:07
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
Est c evrai?
Amusant comme variante du problème des échelles dans un couloir pour un retour de vacances.
La hauteur du point de contact à gauche vaut évidemment 8 et celle de droite \sqrt{28}.
Je travaille avec les surfaces des triangles: S1 est le triangle en haut à gauche, S2 en haut à droite et S3 celui du bas dont la hauteur est h.
S2+S3=24
S1+S3=3\sqrt{28}
S1=(\dfrac{\sqrt{28}}{8})^2.S2.
Une substitution directe donne S3=\dfrac{32\sqrt{7}-56}{3}.
Et comme S3=3h, on trouve le résultat final.
Confirmation de la case réponse: 3.18489.
On pourrait utiliser la virgule comme séparateur en France. 
Merci pour cette énigme.
#23 - 12-08-2013 15:40:50
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
est ve vrai?
Oui rivas, l'usage du point comme séparateur est une fâcheuse habitude d'utilisation de langages de programmation, tous anglophonisés 
#24 - 12-08-2013 19:38:28
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Et ce vrai?
Hum..., oui en effet, 8² = 64 et pas 48  donc du coup, il faut remplacer mes racines de 3 par des racines de 7 ce sera mieux (sans doute une erreur de frappe, ... ) donc du coup, il faut remplacer mes racines de 3 par des racines de 7 ce sera mieux (sans doute une erreur de frappe, ... ) 
Ce problème me rappelle un problème similaire ou la longueur des barres étaient
2m et 3m, on savait que le point de croisement était à 1m du sol, et il fallait trouver la distance qui séparait les murs, et ça dans mes souvenirs c'était beaucoup moins trivial !
Il y a sûrement plus simple.
#25 - 12-08-2013 19:44:09
- SabanSuresh
- Elite de Prise2Tete
- Enigmes résolues : 45
- Messages : 1951
- Lieu: Paris
sEt ce vrai?
@cogito : Ce problème, notre classe l'a eu en Devoir Maison sur le chapitre de Thalès cette année (en 3e).
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum