Un exemple, je fais 110101*11101. Le produit fournit :

* pour les unités : 1*1=1
* pour les deuzaines : 0*1+1*0=0
* pour les quatraines : 1*1+0*0+1*1=2
* pour les huitaines : 0*1+1*0+0*1+1*1=1
* pour les seizaines : 1*1+0*0+1*1+0*1+1*1=3
...

On obtient ainsi 1222231201. Il reste à convertir ce nombre en binaire, on procède en partant de la droite :
* 1
* 01
* 201 donne 001 et je retiens 1
* 2001 donne 0001 et je retiens 1
* 40001 donne 00001 et je retiens 2
...
On obtient finalement 11000000001.

Avec un papier et un crayon, ça se fait sans problème avec des nombres à 20 chiffres.

Pour la première partie :



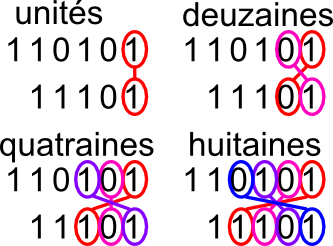
on multiplie les chiffres de la même couleur, et on ajoute tous ces produits.

En fait pour pas que les yeux se croisent, tu suis avec deux crayons, en les déplaçant d'un cran à chaque fois, et lorsque les deux crayons sont sur un "1", tu augmentes le total de 1. Mais bon, j'attends de voir ta méthode, je te crois quand tu dis qu'il y a plus simple.

Le temps est écoulé, je devais une réponse pratique pour la réalisation, j'espère que l'explication sera assez claire.

On suppose les 2 nombres impairs car les zéros à droite des 2 nombres sont simplement additionnés dans le produit.
 
On écrit le premier nombre à l'envers (poids fort à droite) sur une bande qu'on découpe, et on ajoute au 2ème nombre autant ( moins 1) de zéros à droite que de chiffres du 1er nombre.

On prendra soin d'écrire les chiffres des 2 nombres avec le même écartement.

On attribue à chaque chiffre du 2ème nombre la somme des superpositions (1,1) lorsque le 1er nombre est placé au dessus du 2ème, son 1er chiffre à droite étant positionné sur le chiffre à analyser.

Une fois cette opération finie, il ne reste plus qu'à repousser la partie entière de la moitié des sommes sur la case voisine à gauche, opération à commencer à droite. Selon la parité de la somme, on laisse 0 ou 1.