 |
#26 - 25-10-2013 00:18:30
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Un cadeau eigeant
@shadock :Sur chaque coté du carré il y a 3000 côtés alignés.
je viens de modifier le poste précédent.
Il y a sûrement plus simple.
#27 - 25-10-2013 00:27:28
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
un cadeau exigeany
Je ne vois pas trop la subtilité de ton lien, je vois les choses comme ça :

ABCD est-il un polygone? et si D est à l'extérieur relié par un segment au point A par exemple?
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#28 - 25-10-2013 00:32:52
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
un cadezu exigeant
ABCD est un polygone non convexe. Sur ta figure les côtés CD et DA de ce polygone ne sont pas tracés.
Il y a sûrement plus simple.
#29 - 25-10-2013 00:38:04
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Un cadeeau exigeant
Vu comme ça effectivement mais je ne suis pas d'accord pour tes 12000 côtés.
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#30 - 25-10-2013 00:44:47
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
un cadeau exigeany
Sur un côté du carré tu as 3000 points non ?
Il y a sûrement plus simple.
#31 - 25-10-2013 01:08:24
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
yn cadeau exigeant
Et non 12000 justement....
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#32 - 25-10-2013 08:19:12
- Lise-et-Paris
- Habitué de Prise2Tete
- Enigmes résolues : 0
- Messages : 17
Un cadeau xeigeant
On peut toujours trouver la définition qui va coller à l'idée que l'on se fait d'un objet. Selon le dictionnaire des mathématiques de Lucien Chambadal un polygone est une suite de points distincts telle que trois sommets consécutifs ne soient jamais alignés . C'est dans ce sens que nous avions pris ce mot .
De toute façon nous l'avions tous compris comme ça , non ?
#33 - 25-10-2013 12:01:09
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
UUn cadeau exigeant
@Cogito : un carré a quatre côtés, on est d'accord ? Or, si on considère qu'il peut y avoir des "points intermédiaires" et des angles plats au milieu, un carré peut avoir n'importe quel nombre de côtés supérieur ou égal à 4. Un peu ennuyeux. Le fait de pouvoir définir le nombre de côtés et de sommets d'un polygone de façon unique exige d'interdire la présence d'une succession de trois points alignés.
Et c'est une façon d'ergoter sur des définitions d'un niveau élémentaire (pour le plaisir de faire passer ta solution absurde comme valide ?)
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#34 - 25-10-2013 12:30:19
- Lise-et-Paris
- Habitué de Prise2Tete
- Enigmes résolues : 0
- Messages : 17
Un cadeau exiigeant
De toute façon le vocabulaire mathématique n'est pas fixé ad vitam aeternam , il dépend essentiellement du contexte 
Nous aimerions avoir quelques précisions à propos du message de Mathieu :
1°) Pourquoi choisir des vecteurs de sens différent ?
2°) Des vecteurs de somme nulle de sens différents sont-ils nécessairement les côtés d'un polygone convexe ?
3°) En choisissant les plus "petits" vecteurs de sens différents , quelle taille doit-on donner au quadrillage pour qu'il contienne le polygone ?
Nous avons réponse à certaines questions mais pas à toutes 
#35 - 25-10-2013 17:53:58
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Un cadeau exigeat
@shadock : oui mais comme le carré a 4 cotés ...
@Mths-MlndN : Non, si on prend un carré et que on rajout un point intermédiaire alors nous obtenons un pentagone (avec 4 angle droits et un angle plat) et plus un carré (et ce pentagone est unique pour un point intermédiaire fixé).
Sinon j'ai très bien compris que ma solution proposé n'est pas l'objectif de l'exercice, elle n'est pas valide. Je ne pensais pas qu'il y aurait eu tant de controverse sur la définition de polygone.
@Lise-et-Paris : Je ne connaissais pas cette définition. Pardon pour le bruit occasionné.
Il y a sûrement plus simple.
#36 - 25-10-2013 18:27:46
- Lise-et-Paris
- Habitué de Prise2Tete
- Enigmes résolues : 0
- Messages : 17
Un cadea exigeant
Il n'y a pas de mal Cogito 
Si on laisse tomber un moment le quadrillage à 3000 X 3000 points , quelqu'un voit-il une raison qui expliquerait pourquoi , par exemple , on ne peut pas dépasser 10 côtés avec l'exemple initial ?
#37 - 25-10-2013 18:56:03
#38 - 26-10-2013 11:13:16
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
un cafeau exigeant
Pas idiot. La distance totale parcourue lors d'une boucle vaudra au plus le périmètre du domaine carré à parcourir, et les distances des trajets "élémentaires" (c'est-à-dire les longueurs des segments successifs parcourus) sont minorées :
4 segments de longueur 1 au plus
8 segments de longueur 2 au plus (4 droits, 4 en diagonale)
8 segments de longueur 2 au plus (identiques 2 à 2)
etc.
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#39 - 26-10-2013 21:34:00
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
Un cadaeu exigeant
Je vais essayer de répondre aux 3 questions au mieux :
1°) Pourquoi choisir des vecteurs de sens différent ?
Je ne suis pas sûr de la question.
Je précise ma représentation du polygone : je vois un polygone comme une suite de "flèche" mises bout à bout, elles partent d'un sommet du polygone vers le suivant dans le sens de parcours choisi. En soustrayant les coordonnées d'un point au suivant, on obtient les vecteurs qui nous intéresse, représenté par les "flèche" si on fait le dessin.
Forcément chaque fois qu'on s'éloigne du point de départ sur un axe, il va falloir faire le chemin opposé pour retourner au départ : le sens des vecteurs varie. La somme nulle vient de là (le calcul est immédiat en développant la somme des vecteurs avec la différence des coordonnées des points consécutifs)
Mais je pense que vous aviez compris ça.
Peut être que par "sens différent" vous parlez des 8 variations que je fais subir aux couples (a,b).
Intuitivement, on se dit que pour avoir le plus possible de côté, il faut choisir des vecteurs les plus "petit" possible. Si on en trouve un petit, autant utiliser ses 8 autres variantes qui ont la même "taille" (leur somme est nulle).
Avec la contrainte du quadrillage, si un vecteur s'écrit (ka,kb) alors le segment passera par k+1 point du quadrillage (en faisant varier k dans {0,1,2...k} on tombe sur des coordonnées entières), donc on peut réduire la taille du polygone en transformant (ka,kb) en (a,b), et en faisant de même pour (-ka,-kb) qui devient (-a,-b).
C'est de là que vient la contrainte "a est premier avec b" que je rajoute.
2°) Des vecteurs de somme nulle de sens différents sont-ils nécessairement les côtés d'un polygone convexe ?
Absolument! Et je vous remercie pour l'énigme, car c'est en réfléchissant dessus que j'ai trouvé une preuve  : Si on observe un polygone convexe "fléché", les flèches doivent toujours "tourner" dans le même sens. : Si on observe un polygone convexe "fléché", les flèches doivent toujours "tourner" dans le même sens.
C'est a dire pour 4 point consécutif A, B, C, D si l'angle (AB,BC) est positif dans [-pi,pi] alors il en est de même pour (BC,CD), sinon les milieux de [AC] et [BD] seraient de part et d'autre du polygone.
Cette propriété est aussi suffisante pour avoir un polygone convexe (ça doit se montrer par récurrence plus ou moins facilement suivant le baguage théorique à disposition sur la convexité)
Pour obtenir un polygone convexe à partir d'un jeu de vecteur de somme nulle, il suffit donc de ranger ces vecteurs par ordre croissant (ou décroissant) suivant l'angle qu'ils font avec un axe quelconque, puis de les mettre bout à bout dans cet ordre. (Il n'y a donc que deux polygones convexe possibles, symétriques l'un de l'autre).
3°) En choisissant les plus "petits" vecteurs de sens différents , quelle taille doit-on donner au quadrillage pour qu'il contienne le polygone ?
Cette question n'est pas très dure. Pour calculer la largeur, on somme tout les "a" de signe positif trouvés dans les vecteurs (a,b), et pour la hauteur, tout les "b" de signe positif.
C'est pour ça que je range les couples suivant les a+b croissants, car un couple ajoute 2(a+b) à la hauteur et à la largeur en sommant les valeurs positives trouvés dans les 8 variantes.
Voilà, ça fait un post un peut long avec plus de pistes que de véritables preuves, c'est pour ça que j'ai hésité à tout rédiger plus tôt...   
#40 - 26-10-2013 22:08:54
- Lise-et-Paris
- Habitué de Prise2Tete
- Enigmes résolues : 0
- Messages : 17
Un caeau exigeant
Bonsoir Mathieu 
Comme tu l'as sans doute deviné l'objectif principal de nos questions était de t'inciter à clarifier ta stratégie .
Tu as pratiquement tout découvert sauf un point clef ( à notre avis ) : le nombre de côtés est forcément inférieur ou égal à 733 .
A cet égard , l'indice donné par Vasimolo semble pertinent .
Une fois cette borne établie , il restera à trancher entre 732 ou 733 
#41 - 26-10-2013 23:46:04
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
un cadeau exigeabt
Pour reprendre la piste donné par Vasimolo, le périmètre "de Manhattan" du polygone convexe inférieur ou égale à 4x3000 = 12000
Sachant que le nombre de cotés ayant la même longueur de Manhattan L est borné grossièrement par 8L, on doit pouvoir majorer le nombre de coté avec ça.
J'essayerai d'affiner la borne et de faire les calcules demain.
#42 - 27-10-2013 00:05:03
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
Un cadeau exiggeant
En fait en y réfléchissant, on peut se contenter de comptabiliser la longueur de Manhattan cumulé des couples (a,b) où a est premier avec b.
En effet, sans le démontrer, on voit que dans un polygone convexe, un coté ne peut avoir qu'un seul autre coté parallèle au maximum. Donc si on minore les longueurs de Manhattan des cotés, on est amené à prendre des cotés avec les coordonnés premières entre elles correspondant à deux vecteurs opposés (a,b) et (-a,-b) dans ma notation précédente.
On retombe donc exactement sur les vecteurs que j'ai listé dans mon premier post.
Mon polygone avait un périmètre de Manhattan de 4x2993, ce qui laisse 4x7=28 de marge avant la borne 12000.
C'est assez pour caser le 733eme coté puisque la longueur de Manhattan maximal des cotés utilisés s'arrêtait à 23+2 = 25 < 28
Bon, je croix qu'on en est au même point donc... 732 ou 733...
Or arrivé au 732eme coté, la taille du polygone convexe est minoré par 2993-5 sur le plus petit des coté (longueur ou largeur). En effet pour affiner un coté, on est obligé de rallonger l'autre et le périmètre sera forcément plus de 4x2993, puisque le polygone 2993 sur 2993 est optimal pour le périmètre avec 732 cotés pour les raison évoqué précédemment. En se limitant au maximum à 2999 pour la longueur du coté le plus long (on laisse 1 de marge pour le 733 coté, il ne faut pas l'oublier  ), il faut bien que l'autre soit au moins long de 2988 pour que 2999x2+2988x2>4x2993. ), il faut bien que l'autre soit au moins long de 2988 pour que 2999x2+2988x2>4x2993.
Après tous ces chipotages, si on essaye de caser un 733eme coté, on doit rajouter au moins 13 à un des cotés (avec le couple (12,13) de longueur 25). Et la patatra  , c'est le drame, on dépasse de forcément au moins de 1 sur un coté. , c'est le drame, on dépasse de forcément au moins de 1 sur un coté.
Voilà, sauf erreur de ma part, il y a bien au maximum 732 cotés.
#43 - 27-10-2013 09:24:19
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,998E+3
un cadeau exigeabt
De toute façon, tu serais bien en peine de rajouter un segment (2,23), (12;13) ou équivanet vu que cela changerait la parité de ton parcours.
Il faut donc un couple à 26 ou 28, c'est encore pire.
#44 - 27-10-2013 22:27:15
- xmami06
- Amateur de Prise2Tete
- Enigmes résolues : 22
- Messages : 1
nU cadeau exigeant
Voilà une petite énigme pour faire chauffer vos neurones ...
" Je veux dix soldats dans cinq rangs et chaque rang comporte quatre soldats "
PS : Aucun jeux de mots :p
Pour celui ou celle qui à pu trouvé la réponse ( Facile )  m'envoyer un MP ... m'envoyer un MP ...
#45 - 27-10-2013 22:39:47
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,998E+3
Un cadeauu exigeant
La réponse est facile mais là, tu pollues un sujet qui n'a rien à voir.
Pourquoi ne pas le poster en ton nom ?
#46 - 28-10-2013 00:50:18
- Lise-et-Paris
- Habitué de Prise2Tete
- Enigmes résolues : 0
- Messages : 17
Un cadeau exigaent
Nous ne sommes pas convaincus par les arguments précédents en particulier par celui de parité 
#47 - 28-10-2013 09:39:15
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,998E+3
Un cdaeau exigeant
Vous n'êtes pas convaincus de grand chose tous les deux...
Je n'ai pas dit que c'était impossible de rajouter un 733è côté.
J'ai juste dit que la somme des composantes des 732 plus petits vecteurs était de 11972 donc on ne peut pas se contenter d'en rajouter un de 23 vu que cette somme ne peut pas être impaire (il est bien fermé ce polygone ? )
Pour en rajouter un sans dépasser 12000 , soit il fait 26, soit il fait 28 , soit il faut en retirer un de 24 pour en rajouter 2 de 25 de longueur.
#48 - 28-10-2013 09:55:58
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
un cadeau ecigeant
Est-il possible que le nombre soit impair ?
J'imagine mal comment, et le 733 trouvé a-t-il été vraiment vérifié ?
(2 segments alignés n'en font qu'un).
#49 - 28-10-2013 10:12:01
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Un adeau exigeant
Je n'ai pas vraiment compris les raisonnements exposés ici. Mais mon idée était de dessiner une lentille à facettes partant d'un coin du carré au coin opposé. Le parcours retour serait alors symétrique au parcours aller, par rapport à la diagonale ou au point central du carré. En effet, si le parcours aller est optimisé, alors le parcours retour l'est aussi. Ceci impliquerait que le nombre de facettes est pair, mais mon idée de lentille en travers n'est peut-être pas correcte.
#50 - 28-10-2013 10:26:38
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,998E+3
Un cadeau exgieant
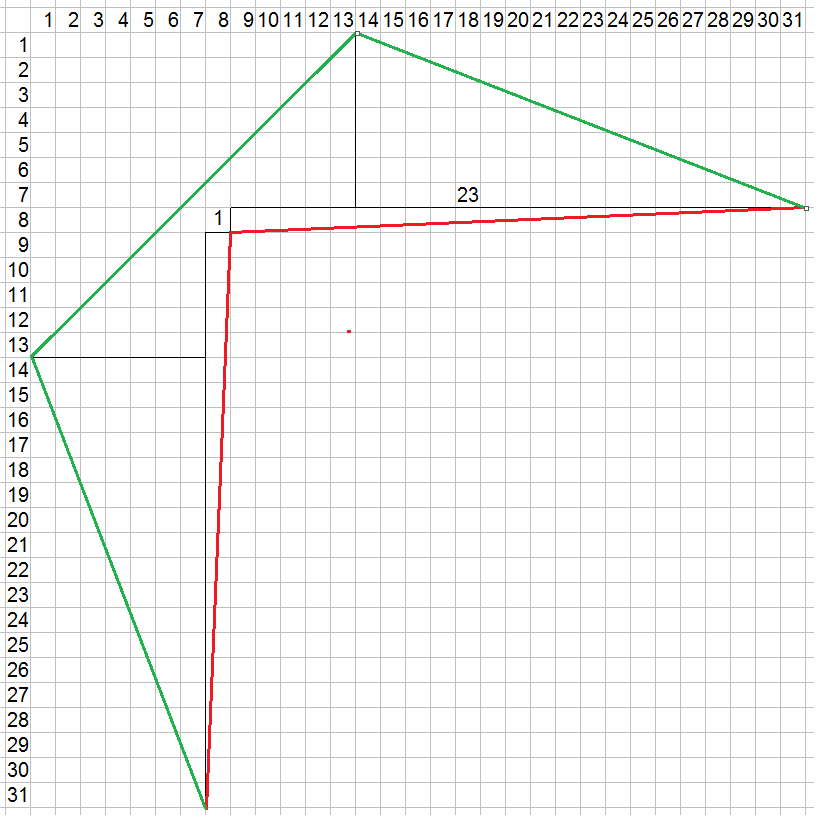
On peut par exemple transformer deux vecteurs de (23;1) en 3 vecteurs de (18;7) , (18;7) et (13;13)
Le total des cases parcourues en ligne et en colonne augmente de 25 +25 +26 -24 -24 = 28
On est alors pile à la limite infranchissable des 3000 tout en n'augmentant la largeur globale que de 7. (mais ça respecte la parité)
Seulement 13 13 est déjà pris par 1,1
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum







