Ton premier exemple n'est pas innocent :

1)  145
2) 1+16+25=42
3) 16+4=20
4) 16+0=16
5) 1+36=37
6) 9+49=58
7) 25+64=89
8) 64+81=145

Et hop, on tourne en rond, ce qui laisse supposer, soit qu'on atteint cette boucle, soit qu'on tombe sur le point fixe 1. Prends ta tête a deux mains, mon cousin, personnellement je ne vois pas encore comment entamer une démonstration

C Bizarre à la fin, les deux termes qui font 89 sont toujours 64 et 25.
Pouvez-vous aussi expliquer ce fait ??
Et aussi Pouvez-vous expliquer pourquoi vers la fin cela fait toujours
?+?=16 ou 61 (chiffres inversés)
1+36 ou 36+1=37
9+49=58
25+64=89
???????????

Après un certain nombre d'opérations, on finit par retomber sur un nombre à 2 chiffres.
Car partant d'un nombre à n chiffres, le suivant est au maximum nx81.

A partir de là, il est normal d'avoir une (ou plusieurs) séquence(s) cyclique(s).
(Il y a au plus 100 combinaisons)

Dans notre cas, ce sont les deux que tu as citées, la première rebouclant sur 8²+9²=145.

On tourne en rond, merde on tourne en rond.
(Bernard Blier, le grand Blond...)

Tu aurais aussi bien pu dire 4 que 89.

D'ailleurs dans ton 1), ta ligne 4 devrait se décomposer en :
4) 4+0=4
5) 16=16

Merci pour ce fait plutot amusant !

pour la preuve, j'avoue être un peu barbare, mais n'ayant pas tout compris au pourquoi de ce joujou ...
il parait évident que si le nombre contient plus de 3 chiffres, le successeur sera plus petit.
en étudiant les nombres a trois chiffres, le plus grand successeur sera dans les 200ish(au pire), le succ de celui ci dans les 100ish(au pire).... et puis ben il suffit de rechercher les 200 nombres qu'il nous reste et de voire qu'il mènent tous à 89 ou a 1

EDIT 89 est le debut du cycle, mais on aurait pu dire qu'ils vont tous a 46 aussi (ou tout autre de la boucle)

Yanyan a écrit:

Merci à halloduda qui a vu une erreur dans l'énoncé.

Oh! Je me réserve la paternité de cette découverte.

Par contre, je n'aurai sans pas le temps de creuser d'avantage. Désolé!

1 est trivialement invariant.
89 fait partie d'un cycle : 89 -> 145 -> 42 -> 20 -> 4 -> 16 -> 37 -> 58 -> 89.

On veut montrer que pour tout n, le procédé atteint soit 1 soit le cycle qui contient 89.

Je teste pour les nombres entre 1 et 243 = 3*9^2.
A la machine ou a la main (pas si long à cause de la redondance des 0 et des palindromes) je trouve que c'est vrai.

L'application du procédé a un nombre de 3 chiffres > 243 me donne un nombre inférieur ou égal a 243 (f(999) = 243).  C'est donc vrai pour tout les nombres de 3 chiffres.

Pour un nombre de n chiffres (n > 3), le procédé donne un nombre de strictement moins de n chiffres.  10^(n-1) - 1 > 9²n 

Donc par récurrence c'est vrai.

Bonjour,

J'imagine bien deux étapes dans une proposition de démonstration

A -Lemme On montrerait que l'opération[latex]f[/latex] "Mettre les chiffres au carré et les sommer" appliquée à un nombre de 4 chiffres ou plus renvoie un résultat inférieur au nombre de départ et qui se stabilise en quelques itérations sur des nombres à 1 ou 2 ou 3 chiffres.


en étudiant le cas de :
[TeX]x=\underbrace{ 999 ........... 9999}_{n \text{ fois le chiffre 9}}[/TeX][TeX]x=\sum_0^n{9*10^n}[/TeX]
soit
[TeX]f(x) = 81n[/TeX]
or
[TeX]{81n}\le{x}[/TeX]
d'où [latex]{f(x)}\le{x}[/latex] pour [latex]{x}\ge{999}[/latex]

(exemple [latex]f(99999) = 5*81 = 405[/latex])

(en fait, je voudrais prouver que cela fonctionne à partir de 100, car 99 est un cas "particulier" avec f(99)=162, plus grand que 99


B - On passe en revue les nombres de 1 à 999 pour balayer l'ensemble des cas et mettre en évidence le caractère cyclique du phénomène.


Quelques essais donnent effectivement soit le cas "2", soit une séquence "atterrissant" ainsi :
....[latex]89\mapsto145[/latex]
et 145 est "cyclique" (ou "congruent" on peut le dire comme cela ?) à lui même

puisque
[TeX]145\mapsto42\mapsto20\mapsto4\mapsto16\mapsto37\mapsto58\mapsto89\mapsto145[/TeX]
Avec une table donnant x²+y², on peut retrouver les antécédents de 145.
Je creuse cette piste en ordonnant les antécédents, je pense ainsi montrer qu'il y a un nombre de séquences limitées.




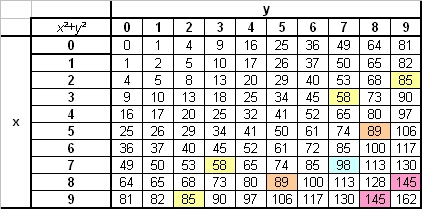
Merci pour cette "curiosité",
A bientôt,

Je viens de lire la preuve qu'à trouver FRiZMOUT sur le net (depuis le temps qu'elle y est je m'apperçois seulement qu'il y avait une suite en bas ).
Cela à l'air de répondre à la question.

Je pense que la plupart de nos énigmes ont une solution sur le net mais ce qui est drôle c'est de chercher sur son petit coin de feuille.

La démo de Nicouj me convient bien. C'est celle que j'aurais tapé si j'avais eu le temps

Pourquoi tester les nombres jusqu'a 243 ? Alors que si un nombre dépasse 100, le résultat sera moindre ?