Vasimolo a écrit:

: La largeur de la boîte est fixée à 4 , peut-on mettre plus de tartelettes dans la boîte que la valeur entière de sa longueur ? Si oui , à partir de quelle longueur et pour combien de tartes ?

Ni la boîte ni les tartelettes ne sont plates comme des limandes.
Si la boîte est assez grande (en épaisseur) , on peut réaliser un étage et le problème est résolu.

Je reste collé à mes 332 tartelettes , il doit y avoir une faille dans mon raisonnement mais je ne vois pas où

Rappel : la boîte est de longueur entière L , de largeur 4 et on veut y ranger L+1 tartelettes . 

On positionne les tartelettes de la façon suivante :



Avec [latex]x=\sqrt{4\sqrt{3}-3}[/latex]

On va donc aligner [latex]k[/latex]  tranches [latex]4\times(x+1)[/latex] contenant chacune 3 tartelettes ( sauf les deux parts extrêmes qui n'en contiennent que 2,5 ) pour une longueur totale : [latex]L=k(x+1)[/latex] .

Le nombre de tartelettes doit être supérieur ou égal à [latex]L+1[/latex] : [latex]3k-2\geq k(x+1)[/latex] donc [latex]k\geq 111[/latex] . Ce qui nous donne [latex]3\times 111-1=332[/latex] tartelettes .

Les positions des centres et des diamètres donnés sur le schéma ci-dessous montrent qu'on ne peut pas améliorer le résultat en supprimant des tartelettes aux extrêmes ( D et F représentent le début et la fin de la boîte ) :



avec [latex]y=x-1[/latex] et [latex]z=\dfrac{\sqrt{3}}2[/latex]

Je me doute bien que je ne peux pas avoir raison contre tous mais je ne trouve pas mon erreur .

En tout cas merci pour la participation , je ne pensais pas que ce problème intéresserait autant de monde .

Après il reste à prouver que le minimum atteint est bien le meilleur et la difficulté risque d'être autre

Vasimolo

halloduda a écrit:

J'ai traité le problème graphiquement avec Geogebra.
Ce programme ne fait pas d'erreurs de calcul.

Moi j'utilise simplement mes deux ou trois neurones qui font sans doute plein d'erreurs mais que je garde précieusement .

Un logiciel ne fait pas d'erreur de calcul , il détient donc la vérité

Vasimolo

Je vois bien que tu argumentes pair-impair depuis le début mais tu as sans doute remarqué qu'ajouter une unique tartelette sur un bord fait basculer cette parité sans doubler la quantité de tartelettes nécessaire .

Vasimolo

J'ai vraiment l'impression que nous ne parlons pas de la même chose

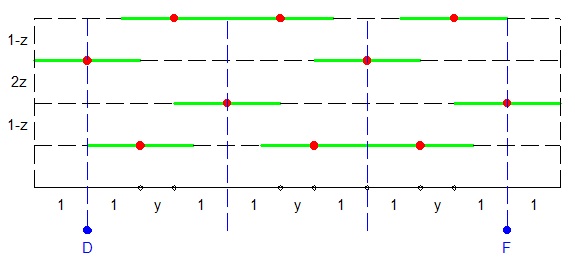
Calculons la longueur de la boîte contenant 167 tartelettes en commençant par la première , la deuxième ou la troisième  .


[TeX]N=1,5+55\times 3+0,5[/latex] et [latex]L=2+55\times(x+1)+1\approx167,008[/TeX]
[TeX]N=0,5+55\times 3+1,5[/latex] et [latex]L=1+55\times(x+1)+2\approx167,008[/TeX]
[TeX]N=2,5+54\times 3+2,5[/latex] et [latex]L=56\times(x+1)\approx166,990[/TeX]
Dans les trois cas on ne met pas 167 tartelettes dans une boîte de longueur 166 .

Vasimolo

C'est bien ce que je disais , nous ne parlons pas de la même chose

gwen27 a écrit:

... La 169e finira à 170 - 56 fois le chouilla soit 170 - 1,009706... = 168,990293855... Dans une boîte de 169 de long, c'est gagné.

Tu fais entrer 169 tartelettes dans une boîte de 169 de long alors qu'il faudrait en faire entrer 170 .

Vasimolo

La demande n'était certainement pas claire au départ mais il me semble avoir précisé à plusieurs reprises que l'objectif était de faire entrer L+1 tartelettes dans une boîte de longueur L .

Tout ça n'est pas bien grave

En fait les deux questions sont intéressantes :

1°) Il faut au moins 167 tartelettes pour que ça rentre dans une boîte de moins de 167 .
2°) Il faut au moins L+1=332 tartelettes pour que ça rentre dans une boîte de longueur L=331 .

Rien n'est prouvé mais je vois mal comment on peut faire mieux .

Vasimolo

Merci pour ton énigme Vasimolo, je l'ai trouvée très intéressante.

Avant de chercher, j'avais même un doute sur l'existence d'une solution.

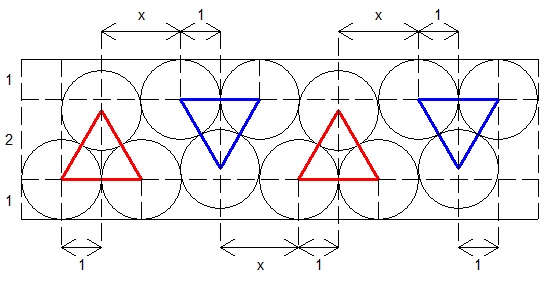
Si je ne me trompe pas, les deux solutions, "en triangle" et en "losange", placent à chaque fois le cercle à l'emplacement le plus à gauche (sauf pour le deuxième cercle).

On pourrait penser qu'en optant à un moment pour un coup moins favorable, il se crée par la suite une opportunité de placement intéressante.