2 joueurs parient qu'il y a un nombre pair de pastilles vertes
et 2 joueurs parient le contraire.
Ainsi les 4 joueurs sont surs de gagner.

Oui, j'avais compris. Les stratégies employées sont explicitement les suivantes :

Pour les joueurs 1 et 2 : S'ils voient un nombre pair de pastilles vertes, ils disent "rouge", sinon ils disent "vert". Les joueurs 1 et 2 devinent leur couleur si et seulement s'il y a un nombre pair de pastilles vertes au total.

Pour les joueurs 3 et 4 : S'ils voient un nombre impair de pastilles vertes, ils disent "rouge", sinon ils disent "vert". Les joueurs 3 et 4 devinent leur couleur si et seulement s'il y a un nombre impair de pastilles vertes au total.

Les joueurs 1 et 2 devinent leur couleur si et seulement si les joueurs 3 et 4 ne la devinent pas. Ainsi les 4 joueurs sont surs de gagner.

Bonjour, alors dans ce cas, ils ont 100% de chance de gagner !

Si on nomme les joueurs A B C D, alors A dis la couleur de B et B dis la couleur opposé de A, C et D font de même.

Si A et B ont la même couleur de pastille alors ils vont annoncer chacun une couleur différente et donc uniquement un seul des deux joueurs donnera la bonne couleur de sa pastille.

Si A et B ont des couleurs de pastilles différentes, alors ils vont annoncer tous les deux la même couleur, et donc là aussi  uniquement un seul des deux joueurs donnera la bonne couleur de sa pastille.

De même pour C et D. Ce qui fait donc que exactement deux joueurs donnera la bonne couleur de pastille.

Il porte bien son nom Gérard Menbon

Argh, oui, effectivement. Bon alors du coup j'ai aussi 5/8 avec la stratégie suivante :

A et B disent la couleur minoritaire si elle est présente, et la couleur majoritaire sinon ; et C et D disent la couleur majoritaire qu'il voient.

Ainsi si on fait une analyse de cas nous avons :

A B C D
V V V V   A, B, C et D disent V : Gérard gagne. 
V V V R   A et B disent R et C et D disent V : A B et D ont faux : Gérard gagne.
V V R V   A et B disent R et C et D disent V : A B et C ont faux : Gérard gagne.
V R V V   A dit R et B, C et D disent V : seuls C et D ont bons : Gérard perd.
V R V R   B et C disent R, et A et D disent V : seuls A et B ont bons : Gérard perd. 
V R R V   B et D disent R, et A et C disent V : seuls A et B ont bons : Gérard perd.
V V R R   A, B, C et D disent V : seuls A et B ont bons : Gérard perd.
V R R R   A, C et D disent R et B dit V : seuls C et D ont bons : Gérard perd.

Donc les joueurs gagnent 5 fois sur 8 (les huit autres cas sont pareils en inversant les V et les R)

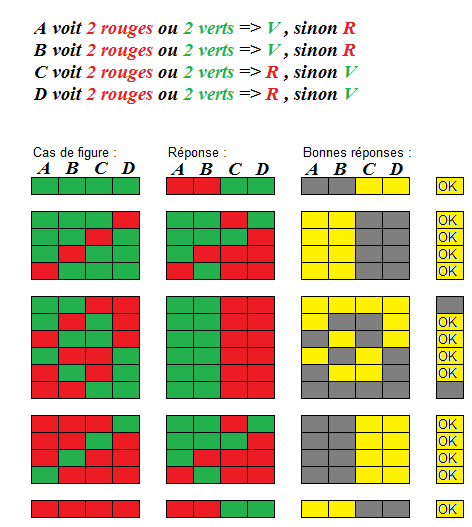
Je pense avoir trouvé une stratégie avec laquelle on gagne 14 fois sur 16.

Peut-on faire 16/16 ? C'est mathématiquement envisageable, mais je ne pense pas.

Oui, je l'ai vu entre temps.


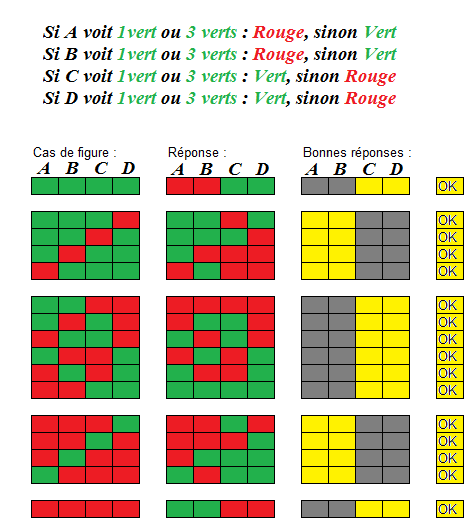
En gros, A et B misent sur une répartition 1 / 3 et gagnent chaque fois qu'on l'a, perdent sinon.

C et D font l'hypothèse inverse et gagnent donc dans les cas ou A et B perdent et inversement.

100% de bonnes réponses potentielles, c'est encore plus de l'arnaque pour le pauvre Gérard

Les joueurs Alain et Bernard décident de donner la couleur qui apparait un nombre pair de fois, Carole et Diane celle qui apparait un nombre impair de fois.
Comme je le disais dans mon post sur l'autre version du jeu, dire la couleur qui apparait un nombre impair de fois permet d'avoir 4 bonnes ou 4 mauvaises réponses.
Si 2 joueurs décident de dire l'inverse il y aura donc toujours 2 et seulement 2 bonnes réponses

scarta:bravo!
fix33:"[pensée intérieure]Attention, méfie-toi, les stats c'est pas ton truc non plus ![/pensée intérieure]"
Je suis d'accord!
fix33:on peut faire mieux que 1/2!

Je viens de me rendre compte que je n'avais pas tout lu dans l'énoncé ! Les joueurs connaissent les pastilles des autres !...