|
#26 - 30-01-2015 20:08:55
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#27 - 31-01-2015 05:59:36
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Gâtea 91
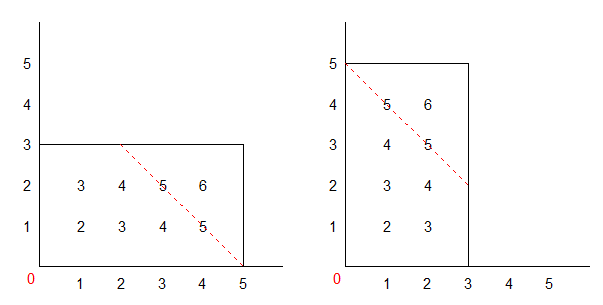
On va placer le 1/2 carré en pointe, diagonale horizontale en haut. On dira que la hauteur est 0 à l'angle du carré en bas.
Soit L et l les dimensions d'une gaufrette, on peut placer 1 gaufrette pour une hauteur de (L+l)/rac2, quel que soit le placement de la gaufrette. Et 2 gaufrettes avec une hauteur (L+2l)/rac2. En fait chaque fois qu'on place une gaufrette, la hauteur de son coin le plus haut est celle de son coin le plus bas augmentée de 1L +1l. Si on continue à remplir le fond du 1/2 carré avec des gaufrettes en prenant la précaution de faire du remplissage convexe, c'est à dire aucune gaufrette posée ne doit dépasser celle qu'elle recouvre, ce qu'on peut tjs faire étant donné qu'on remplit un espace qui s'élargit vers le haut, alors avec une hauteur (kL+jl)/rac2 quelconque (en prenant la précaution que jl reste en deça de kL, et que quand un ajoute 1 L, on ajoute aussi 1 l) on pourra placer tjs le même nombre de gaufrettes, quel que soit leur disposition, soit kj gaufrettes. Ainsi, on est assuré de placer le même nombre de gaufrettes dans les deux 1/2 carrés à l'approche de la diagonale: Surface et nombre égaux, la surface restante est nécessairement partagée en 2 parts égales.
#28 - 31-01-2015 10:00:16
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
fâteau 91
Nous avons à peu près la même approche 
Il y a un petit détail qui ne me semble pas clair : qu'est-ce qui assure que deux remplissages d'un demi-carré ( sans traverser la diagonale ) seront toujours réalisés avec le même nombre de gaufrettes ?
Vasimolo
#29 - 31-01-2015 21:00:49
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,048E+3
Gâtau 91
Le nombre de rectangle coupant la diagonale est constant, je pense. Il est égal au nombre de multiples de a ou b sur la diagonale.
#30 - 31-01-2015 23:01:20
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#31 - 31-01-2015 23:23:04
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,048E+3
âteau 91
Pour moi, ça ne marche pas.
Tu pars avec un postulat disant que 12 est sur la diagonale. OK, mais rien ne situe la position de ton 12 dans les rectangles. Voir ton post #21 et si l'excédent d'aire est unitaire ?
Il manque toujours un élément à la démonstration.
Il y a des pavages de premier triangle qui interdisent le pavage complet du carré.
#32 - 31-01-2015 23:31:25
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Gteau 91
C'est très astucieux je n'y aurais jamais pensé mais il y a des éléments qui bloquent pour moi, je m'y remet demain matin. 
Un promath- actif dans un forum actif
#33 - 01-02-2015 09:51:38
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteaau 91
@Gwen
Ne me fais pas dire ce que je n'ai pas dit . Je pars d'un pavage existant et je dis que pour tout autre pavage du même gâteau les gaufrettes recouvriront exactement les mêmes valeurs ( ça se voit de proche en proche en partant de 0 ) . Ensuite on considère les gaufrettes sous la diagonale du pavage initial ( celles qui sur le dessin ne contiennent aucun point dont la distance à 0 est strictement supérieure à 12 ) . Si leur nombre est différent de celui des gaufrettes au dessus alors en prenant le symétrique du pavage par rapport à la diagonale obtient un nouveau pavage avec un nombre différent de gaufrettes sous la diagonale ce qui contredit le fait que les gaufrettes des deux gâteaux doivent porter les mêmes numéros .
Vasimolo
#34 - 01-02-2015 09:58:46
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
âGteau 91
Compris effectivement c'est astucieux
Qu'as tu en réserve pour le gâteau 100? 
Un promath- actif dans un forum actif
#35 - 01-02-2015 12:45:12
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#36 - 01-02-2015 14:58:44
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,048E+3
Gâteau 1
J'aurais une approche différente du problème, qui permet , de plus, de comptabiliser les rectangles.
Je pars du principe que a et b sont comme premiers entre eux, par proportionnalité, on peut toujours ramener le problème à ça en réduisant le carré.
(des rectangles 6x4 dans un carré de 24, c'est comme des rectangles 2x3 dans un carré de 12)
Il y a alors une maille unitaire 1 x 1 dans chaque rectangle m x n , m et n premiers entre eux..
Chaque rectangle posé (à part le premier) inclut un et un seul nouveau multiple de m dans sa largeur et un et un seul nouveau multiple de n dans sa longueur ce qui définit un point particulier unique dans chaque rectangle.
La grande diagonale contient un certain nombre de multiples de n et/ou m (qui correspondent d'ailleurs aux intersections des deux pavages à orientation unique.)
Elle coupera donc ce nombre de pièces exactement.
J'ai même tendance à dire que c'est valable pour toute diagonale.
#37 - 01-02-2015 17:14:05
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteau 911
Si on veut compter les rectangles traversés par la diagonale ou de chaque côté de celle-ci il n'y a rien de plus simple car ça ne dépend pas de leurs positions . On peut par exemple les ranger tous dans le même sens et le décompte est immédiat .
Vasimolo
#38 - 01-02-2015 17:27:01
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
gâreau 91
Vasimolo a écrit:Je pars d'un pavage existant et je dis que pour tout autre pavage du même gâteau les gaufrettes recouvriront exactement les mêmes valeurs ( ça se voit de proche en proche en partant de 0)
Je n'arrive pas à voir pourquoi. Peux-tu détailler ce passage et ce "de proche en proche" ?
#39 - 01-02-2015 18:00:23
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteauu 91
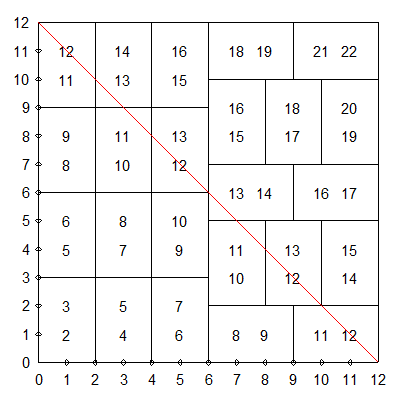
En fait c'est un raisonnement par induction , j'explique pour la grille 12X12 pour ne pas m'embêter avec des lettres 
Quelque soit la position de la première gaufrette dans le coin gauche , elle va recouvrir un point 2 et un point 3 et sa frontière va rencontrer 0123454321 . Il reste un point 2 qui va être le départ d'une nouvelle gaufrette de frontière 2345676543 contenant des points 4 et 5 ...
On peut choisir la position des gaufrettes mais leur contenu est invariant pour la distance Taxicab .
Vasimolo
#40 - 01-02-2015 18:07:29
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
gâteay 91
C'est une récurrence ? Pourrais-tu énoncer clairement la propriété démontrée par récurrence ? Pourrais-tu la démontrer ?
Au départ c'est assez contraint, on voit que l'on doit placer une gaufrette en 2 et une autre en 3, mais l'autre peut a priori se placer en 4 ou 5. Et quand tu es en plein milieu du gâteau, comment savoir où se placent les différentes gaufrettes ?...
#41 - 01-02-2015 18:41:18
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteeau 91
Je ne vais certainement pas rentrer dans une démonstration technique pour entendre en retour que la ligne 3 aurait dû être en 2 
La distance d'une gaufrette à 0 est celle de son coin inférieur-gauche à 0 et on procède en ordre croissant de distances .
Toute gaufrette à la même distance de 0 va recouvrir les mêmes points et sa frontière traverser les mêmes points ( un point étant assimilé à sa distance à 0 ) .
Ce n'est pas clair ?
Vasimolo
#42 - 01-02-2015 19:28:45
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Gâtea 91
Je ne comprends toujours pas. Quelqu'un a-t-il compris ?
Peux-tu faire l'étape 2 sur l'exemple précédent ?
Etape 0 : Une gaufrette en 0, OK.
Etape 1 : Une gaufrette en 2, une en 3, une en 4 ou en en 5
Déjà là, ça pose problème d'avoir un choix non ?
Etape 2 : Quel est le raisonnement maintenant ?
#43 - 01-02-2015 19:38:29
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâtea 91
Tu places les gaufrettes en priorité dans les positions basses .
Vasimolo
#44 - 01-02-2015 20:17:25
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,048E+3
Gteau 91
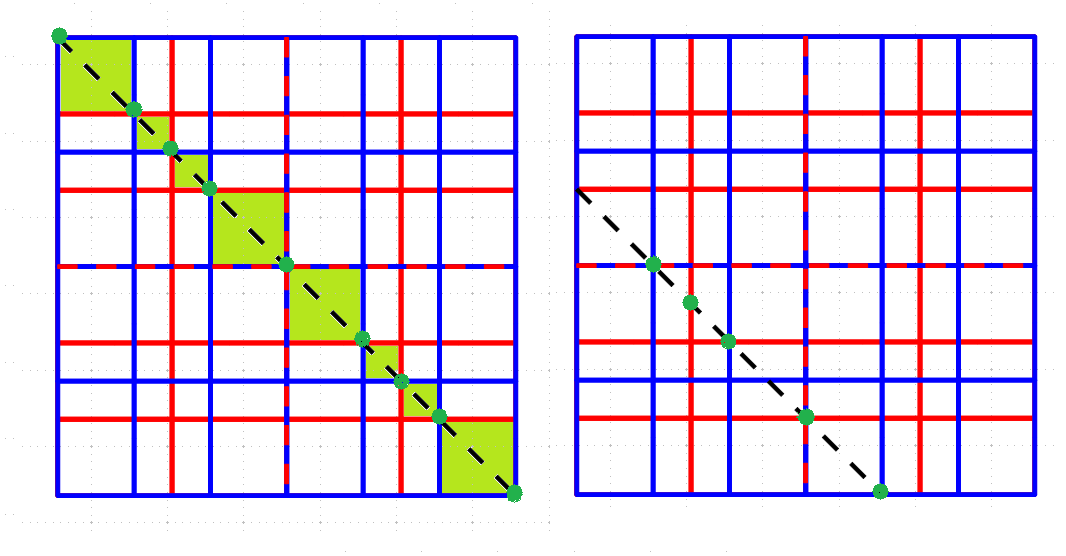
Ces deux demi-pavages permettent tous deux de paver le carré, et les même nombres ne sont pas atteints.
Est-ce du aux formes en jaune ?
Ceci dit, l'un exclut l'autre, tout comme le symétrique de celui du haut s'auto exclut.

#45 - 01-02-2015 21:13:02
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
âteau 91
@Vasimolo : Qu'est-ce que ça veut dire en priorité dans les positions basses ?
Je ne comprends pas qu'il n'y ait pas un argument géométrique à donner quelque part. Par exemple, sur ton exemple, on ne peut avoir deux gaufrettes en position 5, comment justifier ça dans le cas général ? Comment compter le nombre de gaufrettes ayant un numéro donné ?
@gwen : pourquoi dis-tu que les mêmes numéros ne sont pas atteints ?
#46 - 01-02-2015 21:55:20
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
âGteau 91
Ok j'ai compris, il faut uniquement éliminer les points de départs possibles que recouvre une gaufrette et non tous les points qu'elle touche : ce qui compte quand on pose la première gaufrette en 0, ce n'est pas les points qu'elle recouvre ou que sa frontière va toucher, mais uniquement les nouveaux points de départ qu'elle va éliminer : sur l'exemple du haut, ça sera 0(1 fois), 1(2fois), 2(2fois), 3(1 fois). Ensuite, le numéro de départ possible restant le plus petit est obligatoirement occupé par une gaufrette. Les numéros des gaufrettes placées sont donc indépendants de la configuration choisie pour paver le carré.
Merci Vasimolo pour cette jolie énigme.
Pour illustrer ce que je dis sur l'exemple donné plus haut :
Au départ, il y a en positions de gaufrettes possibles : 0 (1 fois), 1(2 fois), 2(3 fois), 3(4 fois), 4(5 fois), 5(6 fois), ..., 19(2 fois)
Il faut une gaufrette en 0 : Ce qui raye 0(1 fois), 1(2 fois), 2(2 fois), 3(1 fois)
Il reste donc 2(1 fois), 3(3 fois), 4(5 fois), 5(6 fois), ..., 19(2 fois)
Il faut donc une gaufrette en 2 : Ce qui raye 2(1 fois), 3(2 fois), 4(2 fois), 5(1 fois)
Il reste donc 3(1 fois), 4(3 fois), 5(5 fois), 6(7 fois), ..., 19(2 fois)
Il faut donc une gaufrette en 3 : Ce qui raye 3(1 fois), 4(2 fois), 5(2 fois), 6(1 fois)
Il reste donc 4(1 fois), 5(3 fois), 6(6 fois), ..., 19(2 fois)
Il faut donc une gaufrette en 4 : Ce qui raye 4(1 fois), 5(2 fois), 6(2 fois), 7(1 fois)
Il reste donc 5(1 fois), 6(4 fois), 7(7 fois)..., 19(2 fois)
Il faut donc une gaufrette en 5 : Ce qui raye 5(1 fois), 6(2 fois), 7(2 fois), 8(1 fois)
Il reste donc 6(2 fois), 7(5 fois), 8(8 fois)..., 19(2 fois)
Il faut donc deux gaufrettes en 6 : Ce qui raye 6(2 fois), 7(4 fois), 8(4 fois), 9(2 fois)
Il reste donc 7(1 fois), 8(4 fois), 9(8 fois)..., 19(2 fois)
etc...
#47 - 01-02-2015 21:58:16
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,048E+3
Gâtaeu 91
Un 14 jaune par exemple dans les coins sortants.
#48 - 02-02-2015 10:41:33
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Gâteau 9
Peut être une version plus simple de la démo.
Soit a et b donnés comme longeur/largeur de la gaufrette et kab le coté du carré. En partant d'un sommet du carré donné à 0, toute longueur rejoignant la diagonale en passant par des horizontales et des verticales mesure exactement kab. Toute gaufrette se situant à une distance (tjs en passant par les H et les V) <kab est incluse dans le demi carré limité par la diagonale). Toute gaufrette s'exprime par une distance max du zéro en ma+nb (m, n non nuls). La configuration: ttes les gaufrettes sont horizontales (ou verticales) permet d'obtenir ts les couples (m,n) tels que ma+nb<kab. On ne peut pas mieux faire. Par symétrie, on peut donc mettre un max de part et d'autre de la diagonale. Il y a même cardinalité max de gaufrettes non coupées de part et d'autre de la diagonale. Toute autre configuration doit nécessairement obtenir ce max de cardinalité, car sinon il y aura du vide sur la diagonale quand on fera le raccord.
Surface de gaufrettes non coupées identique de part et d'autre de la diagonale, donc surface identique aussi de gaufrettes coupées de part et d'autre de la diagonale.
#49 - 02-02-2015 11:49:37
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Gâeau 91
Petite énigme dans l'énigme:
Soit une gaufrette de dimensions a,b (premiers entre eux) et un carré de coté ab. Montrer que sur la diagonale il y a tjs a+b-1 gaufrettes.
C'est un petit problème de pure arithmétique.
#50 - 02-02-2015 14:20:07
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
gâteay 91
@gwen : tu vois bien que les mêmes nombres sont atteints en haut et en bas non ?
@nodgim : Le hic dans ta démo c'est que dans une config quelconque on peut obtenir plusieurs gaufrettes ayant la même distance à zéro avec le même m et le même n, et donc il pourrait être possible de caser sous la diagonale plus de gaufrettes que dans la config où toutes les gaufrettes sont horizontales.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum