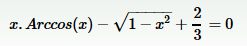Il y a une différence avec le "baguette 2" ?

Je crois que je vais tranquillement attendre 5 ans pour le baguette 4

Mais non je ne suis pas aigri

Vasimolo

Bonjour,
Sauf erreur, je pense avoir trouvé une solution approchée, avec des lames de longueur infinie ayant alternativement une largeur de 1 et 0.219262, et une aiguille de longueur 0.957606 (ou bien une aiguille de longueur 1 et des lames de largeurs respectives 1.044271 et  0.228969)

Voici les probabilités que j'obtiens, par calcul et par simulation (10^7 lancers)
k est le nombre d'intersections de l'aiguille avec un joint

                   calcu         simul        
k= 0           p=  0.3333332089  0.3335252000
k= 1           p=  0.3333337237  0.3331987000
k= 2           p=  0.3333330674  0.3332761000
Total          p=  1.0000000000  1.0000000000

Bravo Enigmatus, j'ai également identifié cette solution.

Voici ma démonstration de l'existence d'une solution. En revanche, je n'ai pas abouti avec un calcul formel des dimensions du motif.

Pour un motif donné, les probabilité P0, P1 et P2 de croiser respectivement 0 fois, 1 fois et 2 fois ou plus les joints sont fonctions de la longueur a de l’aiguille et des caractéristiques du parquet.
On ne réduit pas le problème en utilisant l'aiguille comme longueur unité.

Les 3 probabilités vérifient P0+P1+P2=1, il y a donc une « liberté » d’ordre 2 (P0 et P1 donnés impliquent P2).
On peut donc imaginer qu’un motif défini par 2 caractéristiques variables indépendamment permettra de faire varier (P0 ,P1) dans une partie de [0 ;1]x[0 ;1].

Voici 3 exemples de motifs à 2 paramètres :

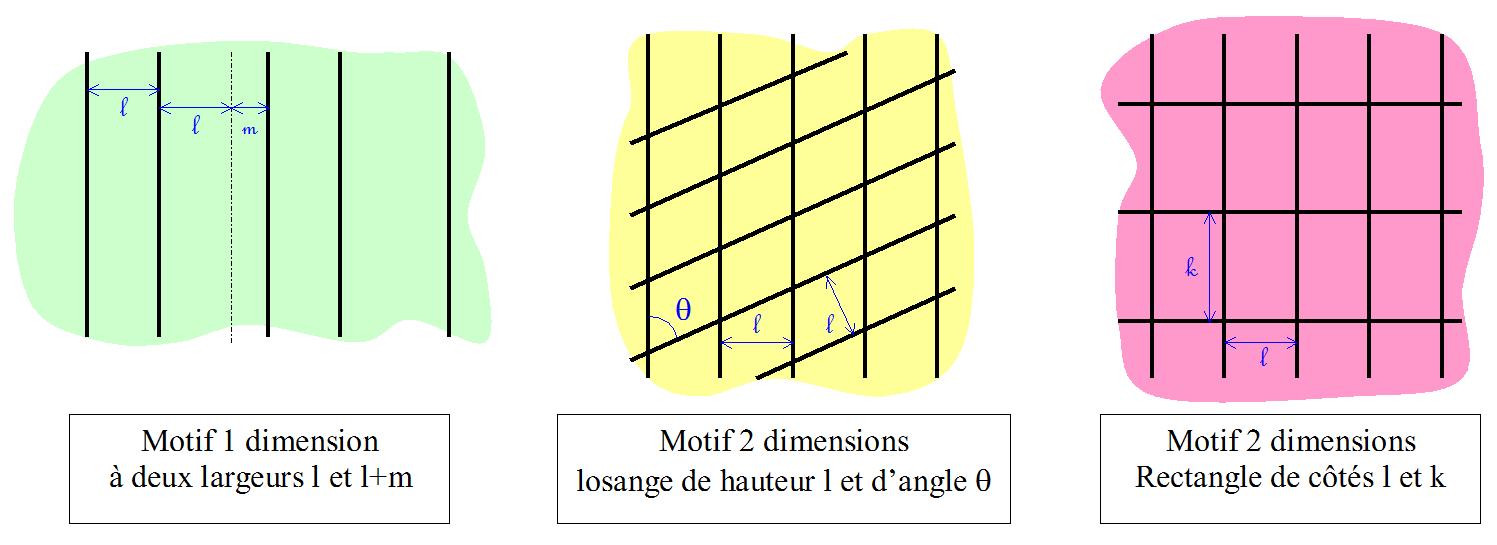
Je me suis uniquement penché sur le premier.

L’expression de la probabilité de ne croiser aucun joint dans le cas de l’aiguille de Buffon sur un parquet à lames identiques de largeur l est connue (http://fr.wikipedia.org/wiki/Aiguille_de_Buffon). Nous l’appellerons Pz(l).
Pz(l)=1-2/(pi*l) pour l >1 et Pz(l)= « une expression plus compliquée » pour l <1.
On peut l’utiliser pour déterminer P0 en fonction de l et m. En effet, lorsque l’aiguille tombe, son milieu est sur une lame de largeur l dans l/(2l+m) cas et sur une lame de largeur l+m dans (l+m)/(2l+m) cas. Donc P0(l,m)= l/(2l+m) Pz(l) + (l+m)/(2l+m) Pz(m+l).

Nous pouvons déjà affirmer que P0(l ;0)=Pz(l) (Prop 1) : quand m=0, on est dans la configuration classique de l’aiguille de Buffon.
Nous avons également P0(0 ; m)=Pz(m) : cas limite où 2 joints sont toujours confondus. On a alors P1(0 ; m) = 0 et donc P2(0 ; m) = 1 – Pz(m) (Prop 2), que l’on va utiliser juste après.

Nous recherchons l et m tels que P0(l,m) = 1/3. Cette expression implicite n’est pas (facilement) retournable. On appelle M(l) la valeur de m solution de P0(l,m)=1/3. M est une fonction continue par construction, sur tout intervalle où elle est définie. En voici une interpolation avec la courbe C, point par point avec un solveur (Excel).



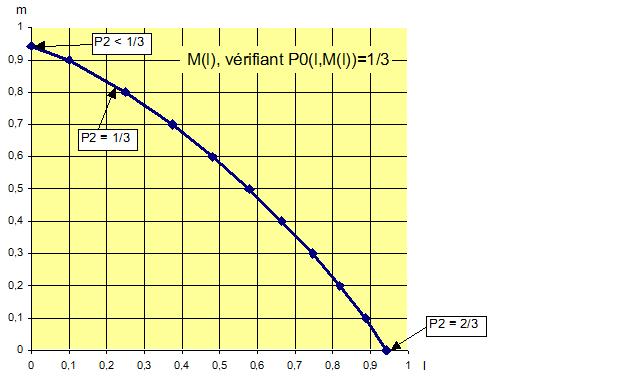
Soit k vérifiant Pz(k)=1/3
On voit sur le graphe que (Prop1) est vérifiée : P0(k ; 0)=P0(0 ; k) = 1/3 et que k~0,94.

La fonction Pz(l) est une fonction croissante de l (par construction, plus la largeur des lames est grande plus on risque de ne croiser aucun joint).
Pz(1)=1- 2/(pi)~0,36>1/3
Pz(racine(2)/2)=1- [2*racine(2)/pi * (1-racine(1-1/2)) + 1 – 2 arcsin(racine(2)/2)/pi ] = 1/3 + (pi+12-12*racine(2))/(6pi)<1/3

Donc k est dans [racine(2)/2 ; 1]

Comment varient P1 et P2 lorsque (l,M(l)) décrit la courbe C ?
D’après (Prop 2), P1(0 ; k) = 0 et P2(0 ; k) = 2/3.

On va maintenant montrez que P2(k ; 0) < 1/3 (c’est assez lourd, mais je n’ai pas vu plus aérien) :
P2(k ; 0) est la probabilité qu’une aiguille lancée sur un parquet simple de largeur k coupe 2 joints.
P2(l ; 0) est une fonction décroissante de l (plus la largeur des lames est grande, moins on risque de croiser 2 joints ou plus).
Pour lr=racine(2)/2, étudions la probabilité de couper 2 joints.
Pour qu’une aiguille coupe 2 joints, il faut que l’extrémité gauche de l’aiguille soit suffisamment près du premier joint croisé (indépendamment de l’angle) Event1 et il faut également que l’angle avec le parquet soit tel que la projection des 2 extrémités soit plus longue qu’une largeur de lame (indépendamment de la position de l’extrémité gauche) Event 2.
Donc P2(lr ; 0) < P(Event 1) * P(Event 2)
Event 1 : dans le cas le plus favorable (angle = 0), l’aiguille coupera 2 lames si l’extrémité gauche est à moins de 1-lr du premier joint croisé, donc P(Event1)=(1-lr)/lr=racine(2) – 1
Event 2 : si l’angle est tel que la projection des 2 extrémités de l’aiguille est inférieure à la largeur du parquet, il n’y a aucune chance de croiser 2 joints. Donc P(Event2)<pi/4/(pi/2)=1/2.
Donc P2(lr ; 0) < racine (2)/2 – 1/2 <1/3

D’après la décroissance de P2(l ; 0), on a donc P2(k ; 0) < 1/3

On va admettre que P2 est une fonction continue de l et m (il n’y a aucune raison qu’elle ne le soit pas !), donc P2(l ;M(l)) est une fonction continue de l. D’après le théorème des valeurs intermédiaires, il existe lc dans [0 ; k] tel que P2(lc ; M(lc))=1/3

On vient donc de démontrer l’existence d’un motif défini par lc et M(lc) tel que P0=P1=P2.

J’ai pu estimer une valeur de lc et M(lc) en simulant des lancers d’aiguilles et en comptant les cas favorables. J’ai trouvé, comme Enigmatus : lc ~ 0,23 et M(lc)~0,81.

... et que la taille de la plus petite lame est l'unique solution de l'équation :



Vasimolo

Un PDF pour pallier à la déficience du LaTeX du site  :