Enigme Dans le carré @ Prise2Tete

kossi_tg · #1

Peut on toujours placer N pions dans un carré de côté N*N sans qu'il y ait 2 pions qui partagent colonne, ligne ou diagonale? Justifiez

Une précision: si on prend le carré comme un damier, les diagonales dont parle le sujet sont toutes celles qui sont parallèles aux 2 principales. Il n'y donc pas que les 2 grandes diagonales mais tous les alignements à-/+45°. Désolé pour la confusion.

Vasimolo · #2

Bonjour

Déjà ça ne marche pas avec n=2

Vasimolo

gwen27 · #3

NON, ça ne marche pas pour 2x2

kossi_tg · #4

Deux cas évidents sont identifiés, N=2 et N=3 où ça ne marche pas.
Dans le cas général, pour un N quelconque, comment savoir si ça marche ou pas?

kossi_tg · #5

Pour info, ça marche pour N=4, 5, 6, 7, ...

nodgim · #6

A part le cas N=2 pas faisable, il suffit de disposer les pions sur les cases voisines d'une diagonale. Si N impair, 1 pion sur la diagonale.
ça marche aussi pour 3 il me semble, kossi.

Vasimolo · #7

C'est une généralisation du fameux problème des huit dames sur l'échiquier .

Il y a plusieurs solutions dès que N est supérieur à 3 . Il y a un algorithme très simple qui donne une des solutions , je devrais pouvoir retrouver ça si personne ne le fait avant moi

Sinon il y a sûrement moyen de simplement justifier l'existence d'une solution mais il ne me saute pas aux yeux

Vasimolo

dylasse · #8

Pour n=1 et n=2, c'est possible.

Supposons que ça marche pour n, on place 2 pions comme sur le dessin ci-dessous :

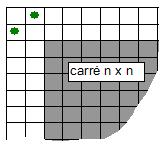
ça marche pour n+2.

Donc ça marche tout le temps !!!

titoufred · #9

Pour N=3, on peut faire :

OXO
OOX
XOO

Ça marche non ?

kossi_tg · #10

Nodim et titouf : n=3 ne marche pas.
Dylasse : ça ne marche pas pour n=2 ni tout le temps.
vasimolo: ce serait très intéressant la solution du cas que tu évoque.

titoufred · #11

kossi, qu'est-ce qui ne va pas dans l'exemple que j'ai donné ? Il n'y a pas deux pions qui partagent la même ligne, colonne ou diagonale !

dylasse · #12

Petite précision...
Est-ce que par diagonale tu entends seulement les 2 diagonales du carré ou tous les alignements à +/-45° ?

Dans le premier cas, ma récurrence est bonne (il faut juste initialiser proprement avec 3 et 4), dans le second cas, il faut que je cherche !

nodgim · #13

Je crois que ça ne marche pas pour les carrés de coté 6k+3 cases.

Franky1103 · #14

Sans la contrainte d'au moins une diagonale (mais juste lignes et colonnes), ce serait possible (par exemple en les disposant justement sur une diagonale).
Avec la contrainte d'au moins une diagonale, ça devient impossible; c'est un peu comme si on avait une inconnue de plus que le nombre d'équations.
Je m'explique: en ayant comme contrainte juste lignes et colonnes, pour le premier pion on aura N² possibilités; pour le second plus (n-1)²; etc ...; et pour le dernier plus qu'une seule. Toute contrainte supplémentaire "bloque" le système.

kossi_tg · #15

Une précision: si on prend le carré comme un damier, les diagonales dont parle le sujet sont toutes celles qui sont parallèles aux 2 principales. Il n'y donc pas que les 2 grandes diagonales mais tous les alignements à-/+45°. Désolé pour la confusion.

Vasimolo · #16

Une solution pour N supérieur à 3 :

1) On note R le reste de N modulo 12 .
2) On écrit les nombres pairs de 2 à N .
3) Si R=3 ou R=9 on met le 2 à la fin de la liste .
4) On écrit les nombres impairs de 1 à N ( sauf si R=8 , on les permute alors deux à deux : 3,1,7,5,...).
5) Si R=2 on échange 1 et 3 et on met le 5 en fin de liste .
6) Si R=3 ou R=9 on met 3 puis 1 en fin de liste .

Par exemple pour N=15 , l'algorithme donne : [4,6,8,10,12,14,2,5,7,9,11,13,15,1,3] .

La ième composante indiquant la hauteur du pion de la ième colonne .

Vasimolo

kossi_tg · #17

vasimolo a écrit :

C'est une généralisation du fameux problème des huit dames sur l'échiquier .

Oui, c'est tout à fait ca.

Nodim: c'est une très intéressante réponse mais pas que...(enfin, il me semble). Est ce le nombre de cases dans le carré ou le côté du carré que tu donnes?

Les autres: l'énoncé n'était pas vraiment clair sur tous les alignements à -/+45°, vous êtes tous partis sur les 2 diagonales du carré. Partie remise

kossi_tg · #18

vasimolo a fait du vasimolo en donnant carrément un algorithme...
Pour le moment, j'admire sans avis. Vous jugerez par vous même

Vasimolo · #19

Je n'ai pas grand mérite sur ce coup : je n'ai fait que recopier un algorithme sûrement connu depuis très longtemps

Vasimolo

nodgim · #20

Je complète ma première réponse en donnant les impossibilités de construction:
coté 3+6k pour les carrés impairs.
coté 2+12k pour les carrés pairs.

Bon, il faudra justifier tout de même.

enigmatus · #21

Bonjour,

nodgim #13 a écrit:
Je crois que ça ne marche pas pour les carrés de coté 6k+3 cases.

Voici un contre-exemple, pour k=1

Code:

 ♛ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅
 ⋅ ⋅ ♛ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅
 ⋅ ⋅ ⋅ ⋅ ⋅ ♛ ⋅ ⋅ ⋅
 ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ♛ ⋅
 ⋅ ♛ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅
 ⋅ ⋅ ⋅ ♛ ⋅ ⋅ ⋅ ⋅ ⋅
 ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ♛
 ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ♛ ⋅ ⋅
 ⋅ ⋅ ⋅ ⋅ ♛ ⋅ ⋅ ⋅ ⋅

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 27-02-2015 09:03:47

Dans le caré

#0 Pub

#2 - 27-02-2015 09:06:20

Dans le arré

#3 - 27-02-2015 09:25:56

Dans le carér

#4 - 27-02-2015 10:00:10

Dans le caré

#5 - 27-02-2015 10:26:10

aDns le carré

#6 - 27-02-2015 10:55:49

dans me carré

#7 - 27-02-2015 11:03:04

DDans le carré

#8 - 27-02-2015 11:37:18

dand le carré

#9 - 27-02-2015 12:57:35

Dans le craré

#10 - 27-02-2015 13:47:10

dans le varré

#11 - 27-02-2015 13:50:54

dans me carré

#12 - 27-02-2015 13:56:46

dzns le carré

#13 - 27-02-2015 16:21:06

dzns le carré

#14 - 27-02-2015 16:44:51

Dan le carré

#15 - 27-02-2015 17:57:01

Dans le crré

#16 - 27-02-2015 18:05:45

dans lr carré

#17 - 27-02-2015 18:12:33

Daans le carré

#18 - 27-02-2015 18:19:53

ans le carré

#19 - 27-02-2015 19:21:31

Dan le carré

#20 - 27-02-2015 19:32:25

Dans le caré

#21 - 03-03-2015 15:52:14

dans le catré

nodgim #13 a écrit:

Code:

Réponse rapide

Sujets similaires

Mots clés des moteurs de recherche

Pied de page des forums