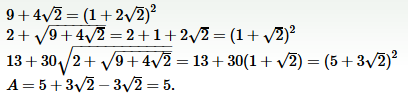Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 02-03-2015 22:44:17
avec les racineqVoilà un petit exercice que j'ai trouvé dans les olympiades des mathématiques et que j'ai aimé le partager avec vous. "Zero is where everything starts ! Nothing would ever be born if we didn't depart from there"
#0 Pub#2 - 03-03-2015 08:43:05#3 - 03-03-2015 19:20:17#4 - 03-03-2015 22:50:18#5 - 04-03-2015 08:05:33#6 - 04-03-2015 09:20:47
Avc les racinessalut. #7 - 04-03-2015 13:53:06#8 - 04-03-2015 21:42:11
avev les racinesBonsoir, Code:B = sqrt(9+4*sqrt(2)) = sqrt((1+2*sqrt(2))**2) = 1+2*sqrt(2) C = sqrt(2+B) = sqrt(2+1+2*sqrt(2)) = sqrt(3+2*sqrt(2)) = sqrt((1+sqrt(2))**2) = 1+sqrt(2) D = sqrt(13+30*C) = sqrt(13+30+30*sqrt(2)) = sqrt(43+30*sqrt(2)) = sqrt((5+3*sqrt(2))**2) = 5+3*sqrt(2) A = D - sqrt(18) = 5 + 3*sqrt(2) - 3*sqrt(2) A = 5 #9 - 04-03-2015 22:45:04
avec les racunesReponse 5 The proof of the pudding is in the eating. #10 - 05-03-2015 15:00:45
Avec les raciesBonjour pour écrire des équations sans latex. L’idée est de se débarrasser des racines carrées (en élevant au carré). A la fin, on a une expression du type: M+N.V2 = 0, ce qui implique: M = 0 et N = 0, puisque M et N sont des entiers. Allons-y: #11 - 05-03-2015 15:17:06#12 - 05-03-2015 20:44:24
avrc les racinesJ'ai bien une méthode plus simple ... avec la calculette, mais je crains qu'elle soit hors jeu. #13 - 15-03-2015 15:37:09Réponse rapideSujets similaires
Mots clés des moteurs de recherche
|
 | ||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.