Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 09-08-2015 20:50:47
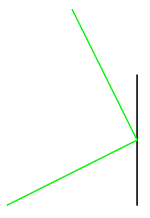
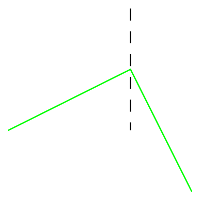
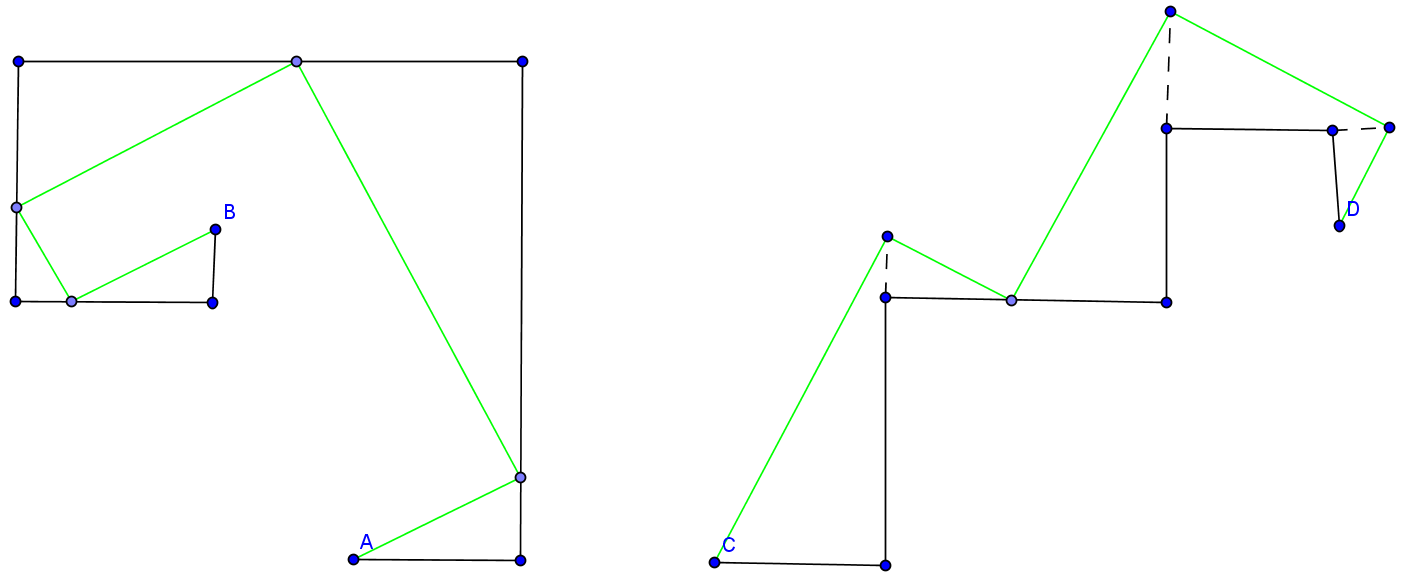
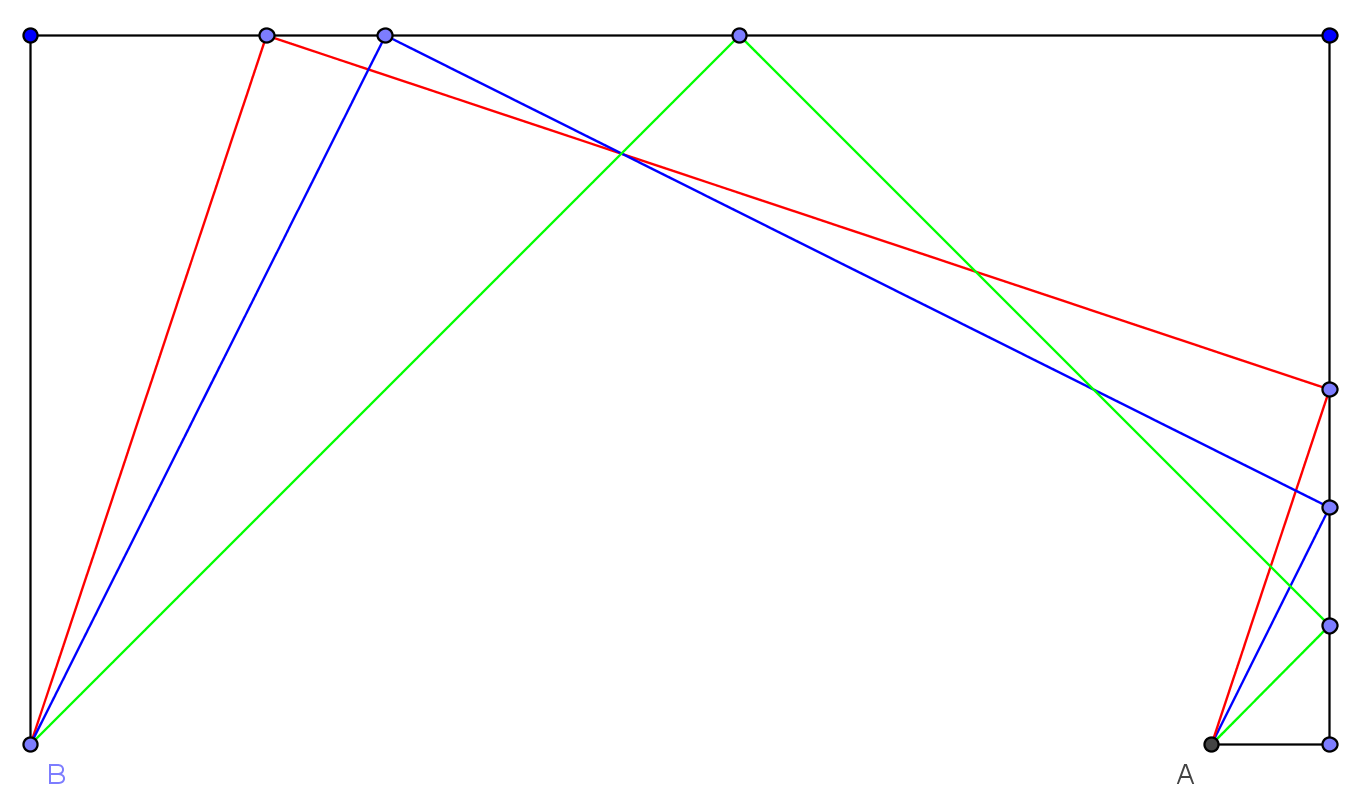
chemins oolynomiauxOn appelle chemin orthogonal de rang N une succession de N segments qui relient deux points du plan et telle que chaque segment est orthogonal au précédent.
#0 Pub#2 - 12-08-2015 16:14:12
Cheminns polynomiauxJe vais commencer mes recherches, cependant j'aimerais que tu rajoutes du temps Un promath- actif dans un forum actif #3 - 13-08-2015 00:29:41
chemind polynomiauxJ'ai rajouté du temps ! #4 - 13-08-2015 08:51:35
chemind polynomiauxJe dirais, comme ça au vu de ce qui se passe quand on fait tourner une droite autour du point départ, que l'arrivée n'est pas tjs accessible (sauf bien sûr si l'arrivée est sur le 2ème segment), mais que quand elle l'est, elle l'est par 2 chemins différents. En effet, à partir du 3ème segment, seule une partie de la droite qui prolonge ce segment est accessible. Et c'est pareil pour les suivants. Donc toute arrivée située sur les parties de droite (prolongeant les segments) accessibles peut être atteinte 2 fois. #5 - 13-08-2015 10:05:14#6 - 13-08-2015 10:27:09
chemins polynpmiauxJe conjecture le résultat suivant sans le démontrer pour le moment: il y a au maximum N-1 chemins de rang N-1. Dans chaque cas on aboutit à une équation polynomiale d'ordre N-1 Un promath- actif dans un forum actif #7 - 13-08-2015 10:37:43#8 - 13-08-2015 12:38:11
chemins polynimiauxBonjour Sydre #9 - 13-08-2015 13:24:06#10 - 13-08-2015 14:05:46#11 - 13-08-2015 14:46:19
Chemins polynomiaxuQu'il ait une solution au moins, donc que ce polynôme soit de rang impair, donc un nombre N pair, mais ça c'est une propriété évidente car le premier segment tracé sera parallèle au dernier et comme on peut donner toutes les directions au premier le résultat en découle... Un promath- actif dans un forum actif #12 - 13-08-2015 16:48:50#13 - 13-08-2015 18:05:18
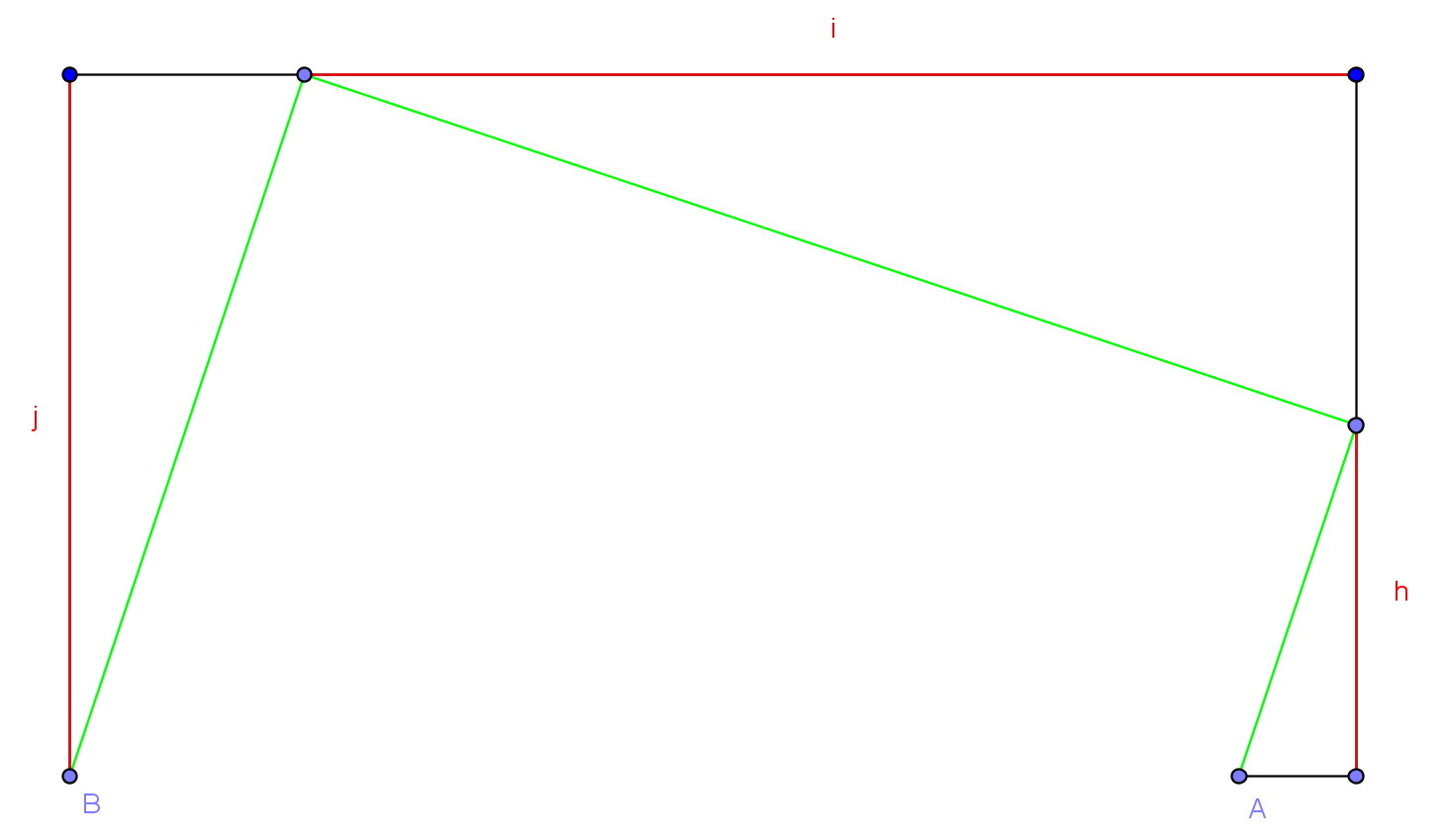
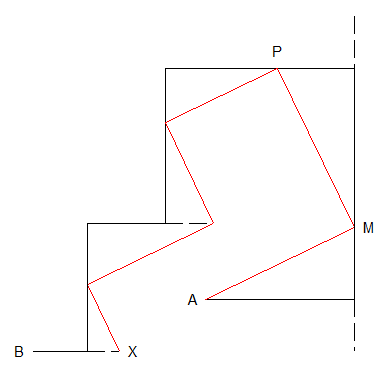
Chemins polynomiauxx"Il y a une autre caractérisation qui mène à des calculs beaucoup plus simples et qui porte sur l'évolution d'une certaine longueur dans certains triangles ..." Un promath- actif dans un forum actif #14 - 13-08-2015 18:23:49#15 - 13-08-2015 19:13:53#16 - 13-08-2015 20:39:02#17 - 14-08-2015 12:50:21
chemins pokynomiauxMmh je ne vois pas ce que tu veux dire par pente caractéristique? Et ce n'est pas possible de trouver le polynôme avec l'équation que j'ai mise en haut de la feuille? Un promath- actif dans un forum actif #18 - 14-08-2015 14:22:14
Chemis polynomiauxTout d'abord bravo à Promath- pour avoir répondu à la question #19 - 14-08-2015 18:30:20
Chemins polynomiauxxUn très joli problème et une très jolie solution Réponse rapideSujets similaires
|
 | ||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.