|
#1 - 11-01-2016 17:34:39
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
#2 - 11-01-2016 17:44:26
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
GGâteau 118
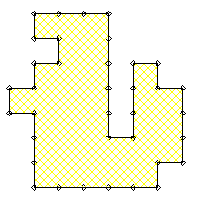
La surface d'un gâteau à côtés impairs est forcément impaire aussi, donc ça ne peut pas marcher.
#3 - 11-01-2016 17:45:03
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
gâyeau 118
Tu en es vraiment sûr 
Vasimolo
#4 - 11-01-2016 18:33:47
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
hâteau 118
Mon affirmation est effectivement fausse: affaire à suivre ...
#5 - 11-01-2016 18:56:45
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâteu 118
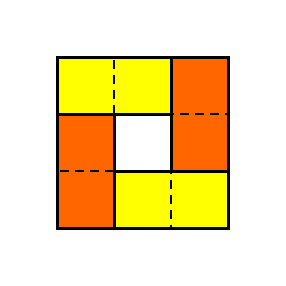
Un gâteau 3x3 avec un trou 1x1 au milieu ?
#6 - 11-01-2016 18:58:55
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
gâteai 118
Non pas de trou , le gâteau est simplement connexe 
Vasimolo
#7 - 11-01-2016 18:58:58
- nobodydy
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1677
Gâteua 118
Salut
Un gâteau avec un trou dans le milieu est il accepté ? Genre moule à savarin !
Edit OK
Je viens de voir le message du dessus, desolé, donc pas de trou 
A suivre....
#8 - 11-01-2016 19:00:38
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteua 118
Les grands esprits se rejoignent : il n'y a pas de trou dans le gâteau 
Vasimolo
#9 - 11-01-2016 19:35:48
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Gâeau 118
Il existe un thèorême qui permet le calcul des aires délimitées par des contours entiers suivant un tel quadrillage. Le connais tu ?
#10 - 11-01-2016 22:05:48
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 181
Tu veux parler du théorème de Pick ?
Vasimolo
#11 - 11-01-2016 23:03:09
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
gâteay 118
Non, pas possible.
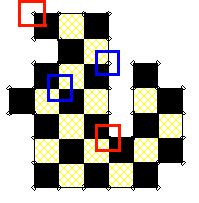
Je commence par colorier mon gâteau en noir et blanc comme un échiquier.
Ensuite, comme mon gâteau est simplement connexe, il n'a qu'un bord. Ce bord est une ligne brisée ; chaque segment de cette ligne brisée est de longueur impaire, donc les carreaux extrêmes de chaque segment sont tous de la même couleur (noir sur mon dessin ; par exemple, le segment du haut touche des cases noire-blanche-noire).
On recouvre ensuite le gâteau par des carrés de même taille que ses carreaux, mais décalés de 1/2 en abscisse et 1/2 en ordonnée. Cela donne des carrés bleus ou rouges.
Les carrés rouges sont ceux qui sont placés sur le bord, autour de l'extrémité d'un segment. Les carrés bleus sont ceux qui sont placés à l'intérieur du gâteau, ou ceux qui sont placés sur un segment du bord, mais pas à une extrémité.
La surface de gâteau recouverte par les carrés bleus est équilibrée blanc/noir. La surface de gâteau recouverte par les carrés rouges est déficitaire en blanc.
Donc au total le gâteau est déficitaire en blanc et il est impossible de le recouvrir par des briquettes autant blanches que noires.
#12 - 12-01-2016 08:28:43
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Gâteau 181
Merci Vasimolo, c'est bien de celui là que je voulais parler. Mais ça ne semble pas aider pour la réponse....
#13 - 12-01-2016 09:30:26
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
GGâteau 118
Bonjour,
Encore un problème impossible.
Si on colorie le gâteau en damier, et que l'on place une case noire sur un coin, tous les segments du bord aboutissant à un coin seront adjacents à une case noire.
On va découper le gâteau en rectangles horizontaux dont les bords droit et gauche sont sur la frontière du gâteau, et de plus grande hauteur possible. Tous ces rectangles auront au moins un coin confondu avec un coin du gâteau.
Le premier rectangle en bas à gauche (il peut en effet y en avoir plusieurs sur la ligne du bas) aura un nombre impair de lignes et de colonnes, donc une case noire de plus.
Ajouté :
Si ce n'est pas le cas, on fait tourner le gâteau de 1/4 tour, et on réessaye. S'il n'ya pas de rectangles à nombre impair de lignes sur un des côtés du gâteau, c'est qu'il y a des trous.
Fin Ajout
Les autres rectangles ont tous une case noire dans au moins un des coins. Ils contiendront donc soit autant de cases noires que de cases blanches, soit une case noire de plus.
Au total, le gâteau aura plus de cases noires que de cases blanches, et ne pourra pas être pavé avec un domino noir et blanc.
#14 - 12-01-2016 12:00:33
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
fâteau 118
@Ebichu : très joli , bravo !!!
@Enigmatus : je ne comprends pas comment tu organises ton découpage .
Vasimolo
#15 - 12-01-2016 12:10:26
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
gâteai 118
juste une direction : faut il :
a)chercher un contre exemple
b) montrer que ce n'est pas possible
Mon intuition m’entraîne sur b) mais gateau 116 me fait douter...
#16 - 12-01-2016 13:09:25
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâtteau 118
Je ne donne pas d'indice pour le moment 
Le fait de ne pas connaître la réponse fait partie du plaisir de la recherche 
Vasimolo
#17 - 12-01-2016 13:56:11
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Gâteua 118
Vasimolo #14 a écrit:@Enigmatus : je ne comprends pas comment tu organises ton découpage .
Voici une illustration avec ton exemple. X et O représentent les couleurs des cases, et tous les rectangles ont un X dans au moins un des coins.
#18 - 12-01-2016 16:19:51
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Gâteua 118
Pour moi, une aire connexe créée avec des rectangles peut toujours se remplir sans qu'on ait besoin d'encastrer un rectangle entre 2 faces existantes. Autrement dit, quand on pose un rectangle, il y a toujours au moins 1 face extérieure. Et comme on crée une construction à partir d'un seul rectangle qui comporte 2 faces extérieures, on ne peut jamais les éliminer. Aussi, une telle construction ne peut pas comporter que des faces de longueur impaire, il y en a au moins 2 paires.
#19 - 12-01-2016 21:38:11
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 18
@Enigmatus : il y a clairement des exemples ou même après rotation , aucun rectangle maximal initial contient un nombre impair de cases .
@Nodgim : je ne comprends pas .
Vasimolo
#20 - 12-01-2016 22:06:51
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Gtâeau 118
Vasimolo #19 a écrit:il y a clairement des exemples ou même après rotation , aucun rectangle maximal initial contient un nombre impair de cases .
Je veux bien en voir un, car je n'en trouve pas.
#21 - 12-01-2016 22:17:47
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteua 118
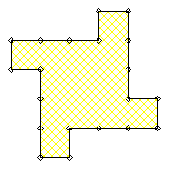
Vasimolo
#22 - 12-01-2016 22:27:20
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Gteau 118
Si, tu as un rectangle constitué d'une seule case.
#23 - 12-01-2016 22:32:10
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâtea 118
Il faut vraiment que tu développes l'enchaînement de la construction de tes rectangles , il me semblait que tu partais de la case la plus basse pour développer le rectangle le plus haut . Si ce n'est pas ça il faut dire quelle est la stratégie que tu mets en oeuvre 
Vasimolo
#24 - 12-01-2016 22:52:13
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Gâteau 11
Ce n'est pas très facile à expliquer. J'oriente le gâteau de façon à avoir en bas un rectangle avec un nombre impair de lignes. Les bords gauche et droit des rectangles sont confondus avec un morceau de frontière du gâteau, et je fais en sorte que leur nombre de lignes soit le plus grand possible.
Exemple :
#25 - 12-01-2016 22:58:35
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteauu 118
C'est un peu ce que j'avais cru comprendre dans tes premiers messages . C'est sûrement vrai mais comment mettre de l'ordre dans tout ça ?????
Sinon on peut chercher une autre piste 
Vasimolo
|
 |

 Accueil
Accueil
 Forum
Forum