 |
#1 - 03-02-2016 18:05:01
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Cheees
Nous retrouvons mon fromager, toujours aux prises avec ses cubes de fromage industriel :
http://www.prise2tete.fr/forum/viewtopic.php?id=12836
Il poursuit ses perforations, armé de son crayon hexagonal, et nourrit toujours son chien avec la partie extraite par le crayon, et son chat avec la partie restante, celle qui est trouée (pauvres bêtes, rongées par le cholestérol).
Considérons un cube (goût saucisson-banane, les meilleurs) : on ne sait pas par avance selon quelle grande diagonale mon fromager va se décider à le perforer. Quel est le volume du fromage dont on est sûr qu'il finira dans l'estomac du chien ?
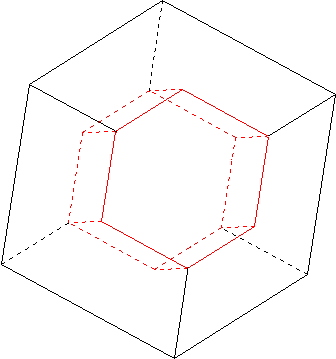
Bon appétit !
#2 - 03-02-2016 18:58:50
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Cehese
Je ne comprends pas bien la question: quelque soit la grande diagonale choisie, le volume reste le même, puisqu'il y a symétrie du cube, non !?!
Je n'ai pas non plus trouvé du cube goût saucisson-banane. 
#3 - 03-02-2016 19:08:50
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
cgeese
@Franky1103 : si tu prends une particule de fromage située près d'un sommet du cube, il est possible qu'elle finisse dans l'estomac du chat, si le fromager choisit de faire passer son crayon par une grande diagonale ne contenant pas ce sommet.
En revanche, une particule de fromage située au centre du cube est certaine de se faire dévorer par le chien, elle se fera éjecter par le crayon à coup sûr ! On demande le volume du fromage qui est dans ce deuxième cas.
#4 - 06-02-2016 12:47:24
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,998E+3
#5 - 06-02-2016 12:55:39
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Cheees
Je viens de comprendre: on cherche le volume qui se trouve à l'intersection des 4 grandes diagonales. Avec ma découpe du cube en 24 pentaèdres de l'énigme précédente, je devrais y arriver: je reviendrai plus tard.
Edit: Je découpe le cube en huit petits cubes identiques, aux rotations et symétries près, constitués chacun de 24/8 = 3 pentaèdres dont un seul est à cette intersection.
Le volume du fromage dont on est sûr qu'il finira dans l'estomac du chien est donc du tiers du volume du grand cube initial.
Re-édit: Je pense qu'on peut aussi raisonner en probabilité. Comme il y a 4 diagonales "exclusives", on a 1 chance sur 4 que cette part n'aille pas au chien.
Soit x la proportion du cube cherchée. On aura: x + (1/4).(1-x) = 1/2, d'où: x = 1/3.
#6 - 06-02-2016 14:57:30
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
vheese
@gwen27 : non, ce n'est pas ça. Quel est ton raisonnement ?
@Franky1103 : non plus ; tu as bien compris l'énoncé, mais je pense que tu surestimes le volume recherché.
On peut commencer à répondre à cette question : quelle est la forme du fromage dont on est sûr qu'il finira dans l'estomac du chien ?
#7 - 06-02-2016 18:08:24
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
cheeqe
Mince ! Avec deux méthodes différentes, je trouve le même résultat ... faux.
Le centre de chaque carré bordant le cube est un point du volume cherché.
Serait-ce alors un octaèdre régulier de volume: V=(V2/3).A³, avec: A=(V2/2).a,
soit: V=(1/6).a³ ?
#8 - 06-02-2016 18:57:01
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
chrese
@Franky1103 : toujours pas, ce n'est pas le bon solide. Par contre, ta phrase contenant le mot "centre" est juste, on progresse. Courage !
#10 - 06-02-2016 22:27:51
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Cheesse
Alors surement un polyèdre étoilé régulier à 14 sommets, 36 arêtes et 24 faces, constitué d'un cube sur chaque face duquel on colle une pyramide de base carrée (égale à une face du cube). Mais j'ai bien du mal à voir en 3D.
#11 - 06-02-2016 22:36:28
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Cehese
@gwen27 & Franky1103 : amusant, vous pensez tous les deux à la même chose dans votre dernier message. Ce n'est pas tout à fait le bon polyèdre, mais vous n'êtes pas loin du tout. Le bon polyèdre est plus simple...
#12 - 07-02-2016 11:20:38
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
vheese
Tout comme le cube et les quatre perforations hexagonales simultanées, le polyèdre cherché a les mêmes axes, plans (y compris les diagonales) et point de symétrie. J'ai beau retourner ce cube dans tous les sens, je retombe à chaque fois sur l'octaèdre régulier de mon post #7, qui n'est pas la bonne réponse.
En conséquence de quoi, en plus de sa part de fromage goût saucisson-banane, le chat reçoit également ma langue.

#13 - 07-02-2016 11:44:58
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,998E+3
chrese
Effectivement, on obtient un dodécaèdre rhombique d'arete : rac(3) /4
et donc, de volume : 1/4

#14 - 07-02-2016 14:23:58
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Cheeese
@Franky1103 : effectivement, on recherche un polyèdre qui a bien ces symétries ; mais ce n'est pas l'octaèdre.
@gwen27 : tout à fait, félicitations !
#15 - 07-02-2016 21:51:30
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Chese
Merci à gwen27 & Franky1103 pour leur participation, et bravo à gwen pour avoir trouvé (et pour sa figure). Effectivement, comme il l'avait observé, la figure obtenue est un dodécaèdre rhombique, dont 6 sommets sont les centres des faces du grand cube, et les 8 autres sont les centres des 8 petits cubes.
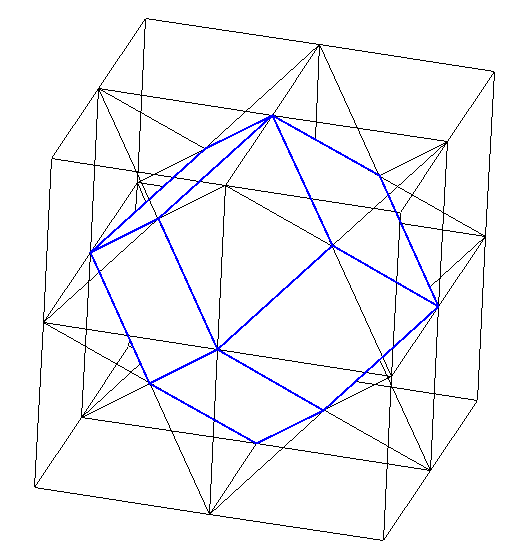
Comment le voir sans logiciel ? On se place dans un des 8 petits cubes, et on étudie son intersection avec les 4 trous de crayon potentiels.
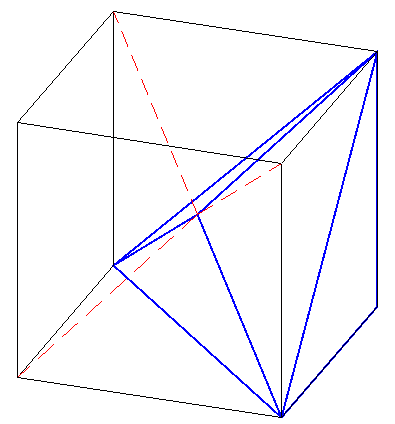
L'intersection du petit cube avec un des 4 trous est égale au petit cube entier. Pour chacun des 3 autres trous, cette intersection est une pyramide dont une base est une des 3 faces du petit cube situées à l'intérieur du grand cube, et dont le sommet est un sommet du petit cube. Sur le dessin, une telle pyramide est par exemple celle dont la base est la face arrière du cube, et dont le sommet est le sommet du cube le plus en bas de l'image.
L'intersection des 3 pyramides donne l'hexaèdre représenté en bleu, hexaèdre qui représente 1/8 du dodécaèdre rhombique. On peut noter que toutes les arêtes de ce dodécaèdre rhombique sont des demi-grandes diagonales des petits cubes.
Pour terminer, le calcul du volume : le volume de l'hexaèdre bleu est 1/4 de celui du petit cube, car on peut recoller 4 hexaèdres bleus pour obtenir un petit cube. La figure suivante montre comment placer les deux premiers. Ceci implique que le volume du dodécaèdre rhombique vaut également 1/4 de celui du grand cube.
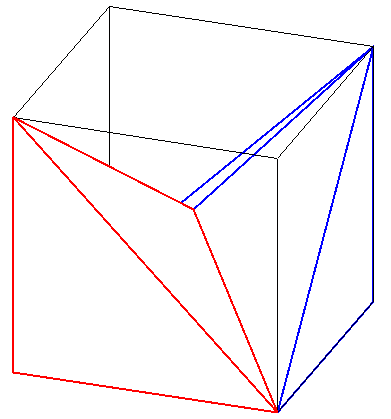
#16 - 08-02-2016 00:10:16
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,998E+3
cjeese
Merci géogebra qui m'a permis de voir la coincidence de certains angles.
#17 - 08-02-2016 09:43:00
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Chees
Merci à gwen27 et à Ebichu pour leurs figures: je comprends mieux maintenant. Un dodécaèdre rhombique est un polyèdre à 12 faces (toutes losanges), à 24 arêtes et à 14 sommets. J'avais bien ces 6+8=14 sommets, mais je ne suis pas arrivé à conclure.
|
 |

 Accueil
Accueil
 Forum
Forum










