 |
#1 - 25-07-2016 22:11:06
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Ô taon suspeds ton vol
Je suis tombé sur ce curieux petit problème cet après-midi .
Un taon se déplace d'un mètre , il tourne de 30° dans le sens direct puis il se déplace de deux mètres , il tourne de 30° dans le sens direct puis se déplace de trois mètres , ... , il tourne de 30° dans le sens direct puis se déplace de 2016 mètres . A la fin de son vol , à quelle distance se trouve-t-il de son point de départ ?
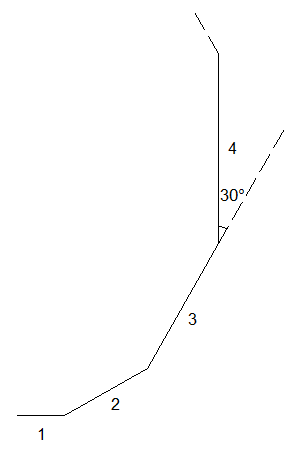
Le calcul peut paraître monstrueux mais il se fait aisément à la main et sans effort sauf pour la touche finale si on veut une valeur approchée .
Je propose une case réponse arrondie à l'unité la plus proche ( avec réserves car je n'ai pas vérifié mon calcul ) .
Amusez-vous bien 
Vasimolo
#2 - 25-07-2016 23:01:02
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Ô taon suspends ton ol
Bon il est tard, je n'ai pas dit mon dernier mot mais c'est un début. Par contre pour faire le calcul à la main ce n'est peut-être pas la bonne idée.
On se place dans le plan complexe Spoiler : [Afficher le message] oui je sais qu'à l'heure qu'il est ce n'est pas une bonne idée  et on définit l'origine par a0=0+0i. et on définit l'origine par a0=0+0i.
On suppose que le taon tourne de ϕ degrés à chaque fois.
On a donc si mes calculs sont bons :
an=(n−1∏k=1ak)×exp(i(n−1)ϕ)+n!×exp(i(n−1)ϕ)
Dont-il "ne reste plus qu'à prendre le module" voilà voilà 
Bonne nuit !
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#3 - 26-07-2016 00:39:21
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Ô taon duspends ton vol
Je sais que les vecteurs ne sont plus beaucoup enseignés de nos jours , mais là les complexes ne font vraiment pas le poids 
J'en ai mis un peu à la fin de mon brouillon ( des complexes ) mais on doit pouvoir aisément s'en passer 
Vasimolo
#4 - 26-07-2016 08:37:17
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Ô taon suspends ton vvol
Bonjour,
Après 12 déplacements, le taon s'est déplacé de 6 mètres vers la gauche, et de 6∗(2+√3)=22.392 mètres vers le bas, soit une distance de 12√2+√3=23.182 mètres.
Après 2016 déplacements, le taon aura fait 168 tours, et sera à une distance de 2016√2+√3=3894.613 mètres de son point de départ.
Sauf erreur bien sûr, car ça ne valide pas la case réponse…
#5 - 26-07-2016 10:01:56
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,066E+3
Ô tzon suspends ton vol
En prenant les opposés, on a toujours une différence de 6. cela se répète 2016/12 fois.
Ca tombe bien, 2016 est divisible par 12...
On arrive à 1008.
La distance est donc le diamètre d'un dodécagone de côté 1008, soit
2016 / rac( 2 - rac(3)) = 3894,61...
#6 - 26-07-2016 11:14:11
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Ô taon ssuspends ton vol
Bravo Enigmatus et Gwen 
Vasimolo
PS : j'ai corrigé la case réponse qui était mal arrondie 
#7 - 26-07-2016 13:12:03
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Ô taon suspendds ton vol
OK alors avec la bonne case réponse je suis rassuré 
On trouve 2016.rac(2+rac(3)), et effectivement, ça se simplifie bien.
#8 - 26-07-2016 13:56:41
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Ô taon suspends on vol
bonjour.
une réponse:
d=2016×√2+√3≈3895
#9 - 26-07-2016 17:36:24
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Ô taon uspends ton vol
3894.612932
Se fait facilement avec un tableur.
Sinon, les incréments sont 1,2x, 3x², ..., 2016x^2015, avec x=e^(i*pi/6)
dont la somme est l'affixe du point d'arrivée et la dérivée de x+x²+x³+...+x^2016
Cette expression est égale à (x^2017-1)/(x-1), dont on sait calculer directement la dérivée.
Il ne reste plus qu'à calculer la longueur du segment (-1008 -3761.907214)
NB x^2016=1
#10 - 26-07-2016 17:59:31
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3234
- Lieu: Luxembourg
Ô tao nsuspends ton vol
Chaque tour de spirale est composée de 360/30=12 segments.
Génial: 2016 est divisible par 12: ça facilitera les calculs.
A chaque tour, l'abscisse diminue de 6, l'ordonnée diminue de 6.(2+V3) et
la distance au point de départ augmente de V(dx²+dy²) = 12.V(2+V3) que
l'on peut aussi écrire 6.(V6+V2)
Au bout de 2016/12=168 tours, cette distance sera de 1008.(V6+V2) soit
env. 3895, validé par la case-réponse.
#11 - 26-07-2016 18:23:18
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Ô taon suspend ston vol
Que du bon 
On peut bien sûr obtenir le résultat avec un tableur ou en résolvant une horrible équation . Personnellement j'aime bien les plaisirs simples et je vois que je ne suis pas le seul .
Vasimolo
#12 - 26-07-2016 20:11:30
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
Ô taon suspends otn vol
Si le mouvement est plan, les coordonnées cartésiennes du taon varient à chaque étape des quantités :
Δx1=1
∀n≥2,Δxn=ncos(nθ)
Δy1=0
∀n≥2,Δyn=nsin(nθ)
Ce qui nous donne en partant de l'origine après n déplacement :
x=1+n∑k=2kcos(kθ)
y=n∑k=2ksin(kθ)
Et donc :
d=√(1+n∑k=2kcos(kθ))2+(1+n∑k=2ksin(kθ))2
Quantité que l'on doit pouvoir écrire explicitement après des calculs laborieux à base d'exponentielle complexe 
Application pour n=2016 et \theta = 30° :
d = \frac{\sqrt{2}}{2}(2017 \sqrt{3} + 2015) \approx 3895 \mathbb{m}
#13 - 27-07-2016 01:18:35
- Smok2k
- Habitué de Prise2Tete
- Enigmes résolues : 27
- Messages : 13
Ô taon suspends tin vol
Bonsoir,
Soit l le vecteur défini par le point de départ (point 1) et le point d'arrivée (point 2016).
Alors, l=\sum_{1}^{2016}{{U}_i} avec {{U}_i} le vecteur défini par le point i et par le point i+1
Or, {U}_i=\begin{pmatrix} i*cos[(i-1)30]\\i*sin[(i-1)30] \end{pmatrix}
Donc, l=\begin{pmatrix} \sum_{i=1}^{2016}{i*cos[(i-1)30]}\\\sum_{i=1}^{2016}{i*sin[(i-1)30]} \end{pmatrix}
Ces deux sommes se calculent assez aisément en passant par les séries entières et les formules d'Euler.
Finalement, on obtient -1008 pour la première somme et -3761,9 pour la deuxième.
Soit, finalement, l=\sqrt{(-1008)^{2}+(-3761,9)^{2}}
Soit l=3895 m, arrondi à l'unité supérieure.
#14 - 27-07-2016 17:16:13
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3827
Ô taon suspends toon vol
Salut Vasimolo,
Est ce un problème qui pourrait être proposé aux 3èmes ? Je ne sais plus si les sommes vectorielles sont abordées au collège...
3895 est validé.
Bien sûr on ne va pas calculer toutes les coordonnées des points intermédiaires, car une somme vectorielle est commutative.
Le calcul est facilité par le fait qu'il n'y a que 12 orientations de vecteurs. Donc on fait le calcul de tous les vecteurs de même orientation. En constatant que 2016 est un multiple de 12 (168 fois 12) on se rend compte qu'on fait 168 "tours" complets. Et chaque tour décale de façon identique le point origine. Le point origine est décalé de 12V(2+V3) donc 168 fois cette valeur donne la réponse. A noter que tous les points intermédiaires de rang n+12k sont alignés.
#15 - 27-07-2016 17:45:28
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Ô taon suspends ton vpl
Tout est bon avec des méthodes très variées mais pas toujours élémentaires .
@Nodgim : les vecteurs ne sont plus enseignés au collège depuis longtemps . Curieusement l'an prochain on retrouvera les translations , les rotations et même les homothéties ( on n'arrête pas le progrès  ) dans les programmes de 3ème . ) dans les programmes de 3ème .
Disons qu'avec un programme de troisième d'il y a 10 ans ( peut-être un petit peu plus ) on peut résoudre ce problème intégralement et sans calculatrice .
Bon courage à ceux qui cherchent encore 
Vasimolo
#16 - 28-07-2016 20:04:10
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
Ô tao nsuspends ton vol
I've started learning Python  , so here we go , so here we go
La réponse est 3894.6129315982894
The proof of the pudding is in the eating.
#17 - 28-07-2016 23:24:14
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Ô taon suspends ton vok
gwen27 a écrit:En prenant les opposés, on a toujours une différence de 6. cela se répète 2016/12 fois.
Ca tombe bien, 2016 est divisible par 12...
On arrive à 1008.
La distance est donc le diamètre d'un dodécagone de côté 1008, soit
2016 / rac( 2 - rac(3)) = 3894,61...
Des réponses élégantes données par Gwen j'en ai vu des dizaines de le temps que je suis sur ce forum mais celle-ci me laisse bouche bée. 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#18 - 29-07-2016 00:05:00
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
#19 - 29-07-2016 00:14:24
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3234
- Lieu: Luxembourg
Ô taon ssupends ton vol
On peut noter que la solution 2016.V(2+V3) peut aussi s'écrire 1008.(V6+V2).
Dans quelles conditions peut-on ainsi simplifier la racine située sous une racine ?
(je n'ai pas la réponse, mais je me posais déjà la question avant cette énigme)
#20 - 29-07-2016 01:12:31
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Ô taon suspnds ton vol
Il faudrait préciser ta question , le cas général est sûrement sans fond 
Avec a,b,c,d entiers , ça c'est déjà pas mal : \sqrt{a+\sqrt{b}}=\sqrt{c}+\sqrt{d}
Vasimolo
#21 - 29-07-2016 15:37:49
- Smok2k
- Habitué de Prise2Tete
- Enigmes résolues : 27
- Messages : 13
Ô taon suspends ton ovl
Haha, je me sens bête d'être passé par un calcul de sommes quand on pouvait conclure en 3 lignes.
Ca m'aura au moins rappelé la prépa et ces bonnes vieilles séries entières 
#22 - 29-07-2016 17:36:50
- Agid1915
- Passionné de Prise2Tete
- Enigmes résolues : 0
- Messages : 50
Ô taon suspends to vol
Pour eviter que le poseur d`enigme dise n`importe quoi apres avoir recu des reponses diverses, il faut introduire une regle stricte :
- envoyer la solution detaillee aux administrateurs du site, a plusieurs de preference au moins 2.
- envoyer un historique bref de la construction de l`enigme si elle est originale ou donner le site ou l`enigme a ete POMPEE.
Sinon, c`est la porte ouverte aux mythomanes pathologiques.
Vasimolo a ete pris la main dans le sac par Bell63 (alias Agid1915)
Il a recopie texto la solution sur AOPS en disant avoir fourni un gros effort.
Faut faire le menage si vous voulez que le site soit credible.
#23 - 29-07-2016 19:07:33
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Ô taon suspends ton vo
Agid1915, tu passes ton temps à critiquer ce que les gens font, tu t'intéresses plus à la vie de personne que tu ne connais pas, qu'à nous laisser tranquille. C'est dérangeant de lire tes commentaires qui sont de véritables attaques.
Si ça t'amuse de faire des comparaisons tu peux les garder pour toi, personnellement même si je vois une énigme similaire sur un autre site, je ne cherche pas à savoir qui à eu l'idée le premier ou pas. Si des problèmes n'ont pas été proposés sur ce site et bien tant mieux si des gens qui les ont vu ailleurs et trouvés intéressants les partages. Je ne vois pas l'intérêt de spécifier le site d'où elle vient. Qui te dit que sur le site d'où elle vient, elle provient déjà d'un site que tu ne connais pas ou d'un livre.
Très franchement les gens qui passent leurs temps à critiquer ce que font les autres, à moins qu'il n'est pas de vie ni d'ami je ne vois pas quel plaisir il pourrait en tirer.
Il vaudrait mieux que tu participes à l'actualité du forum en proposant une énigme originale qui n'a pas été proposée sur ce site et qui n'a pas été proposée sur un autre non plus. Si possible tu nous cites de manière exhaustive tous les sites d'énigmes que tu connais, on passera d'abord du temps à vérifier ce que tu proposes et si ce n'est pas conforme à tes attentes on ne t'insultera, on te demandera gentiment de passer ton chemin et d'aller voir ailleurs.
Vieux mec 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#24 - 29-07-2016 19:33:02
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3234
- Lieu: Luxembourg
Ô tapn suspends ton vol
@Vasimolo
Je pensais effectivement aussi à: V(a+Vb) = Vc + Vd
On trouve: c = [a-V(a²-b)] / 2 et d = [a+V(a²-b)] / 2
Ces nombres sont positifs  , mais pas nécessairement , mais pas nécessairement
rationnels  . .
@Bell63 (alias Agid1915)
Personnellement ce site me convient comme il l'est et
j'y suis presque tous les jours.
#25 - 30-07-2016 00:47:04
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
Ô taon supends ton vol
Agid1915 a écrit:Faut faire le ménage si vous voulez que le site soit crédible.
Commençons par bannir ce guignol du forum, c'est pénible de devoir supporter sa pollution à chaque sujet.
|
 |

 Accueil
Accueil
 Forum
Forum








