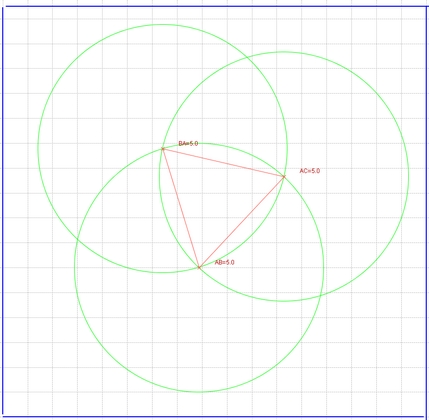
On peut considérer la surface rose comme un triangle équilatéral auquel sont rajoutées trois sections de cercle similaires à celle de l'image suivante :

Le plus simple est de calculer l'aire formée du triangle équilatéral ET d'une de ces sections, puisque l'"alliance" des deux est une section angulaire du cercle, d'un angle de 60° (puisque le triangle est équilatéral) et d'un rayon de 5cm, normal quoi. L'aire de la surface en rose s'obtiendrait alors en partant de trois fois l'aire de cette "section angulaire de cercle" d'angle 60°, qui correspond à trois fois le triangle équilatéral + trois fois la petite section de cercle qui dépasse ; on enlève à cette valeur deux fois l'aire du triangle équilatéral (qu'on a compté trois fois au lieu d'une), et le compte y est. Au final, l'aire recherchée est :
A = 3 * A(section d'angle 60°) - 2 * A(triangle équi)
Trois fois l'aire d'une section d'angle 60°, ça donne l'aire d'une section d'angle 180°, soit un demi-cercle, donc PI * R² / 2. Le triangle équilatéral fait 5cm de côté, grâce à Pythagore on lui trouve une hauteur de 2,5 sqrt(3) cm, et aire d'un triangle = Bh/2. DONC :
A = PI * 5²/2 - 2,5 * sqrt(3) ... le tout en cm².
Soit environ 17.62 cm².
(Pas sûr du tout, peux-tu confirmer ou infirmer ma réponse par MP STP ?  )
)
EDIT : après quelques calculs supplémentaires, la valeur que je trouve me semble réaliste. A voir, donc.

 Accueil
Accueil
 Forum
Forum