 |
#26 - 26-10-2016 22:50:29
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
gâtrau 128
Je note que l'on peut toujours inserer un triangle n*n*n dans un pentagone convexe n*n*n*n*n mais également dans un heptagone (7 cotés), un enneagone (9 cotés) et un hendécagone (11 cotés)...
Mais pas forcement dans un hexagone (6 côtés), un octogone (8 côtés), un décagone (10 côtés) ou un dodécagone (12 côtés) qui peuvent être "plat"...
ou vais-je un peu trop vite en besogne?
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#27 - 26-10-2016 23:12:13
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
âteau 128
Tu es sûr Dan , j'ai l'impression que plus on ajoute des côtés ( pairs ou impairs ) et plus on gagne en souplesse . On doit pouvoir aplatir le truc pour empêcher l'insertion du triangle .
Vasimolo
#28 - 26-10-2016 23:17:08
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Gâtea 128
Ca peut faire l'objet d'une extension à cette énigme...
Mais je pense que non, qu'on ne peut pas aplatir de telle maniere qu'on ne puisse plus inserer un triangle dans un polygone de taille impaire.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#29 - 27-10-2016 08:34:21
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Gâteauu 128
En effet, avec un nombre pair de cotés, on peut faire un parallélogramme aussi plat que l'on veut.
#30 - 27-10-2016 11:38:12
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
GGâteau 128
Je donne raison à Dhrm77, on ne peut pas aplatir un polygone à 2n+1 cotés de longueur 1, à moins d'une hauteur d'un triangle équilatéral de coté 1. Ce min est obtenu avec un trapèze. Mais la preuve....
#31 - 27-10-2016 12:49:26
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
gâtrau 128
En tout cas après 15 côtés , pair ou impair , ça ne passe plus :
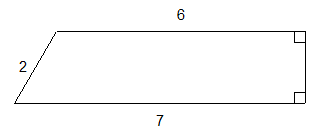
( 2 est le côté du triangle equilatéral ) .
Il reste à traiter les cas : 7 , 9 , 11 , 13 et 15 , pourquoi pas ?
Vasimolo
#32 - 27-10-2016 13:19:51
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Gteau 128
Tu me surprends ici. Dans on problème original on avait un triangle de 9x9x9 et un pentagone de 9x9x9x9x9. ou si on simplifie... 1x1x1 et 1x1x1x1x1.
Ici pourquoi changer le triangle pour un 2x2x2 et garder un polygone de 1x1x1x1x1x1x1x1x1x1x1x1x1x1x1 ?
Si tu gardes le côté du triangle de la même longueur que le côté du polygone, alors ca passe toujours pour un polygone de taille impaire (inférieure ou supérieur a 15...).
Pour que ca ne passe pas, il faut le dessiner concave quelque part...
et dans ton dessin, le segment a droite fait [latex]\sqrt{3}[/latex] ...
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#33 - 27-10-2016 16:08:13
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Gâteau 12
Et bime dans les dents 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#34 - 27-10-2016 17:18:42
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 1228
Pour des raisons de symétrie je n'avais représenté que la moitié du polygone 
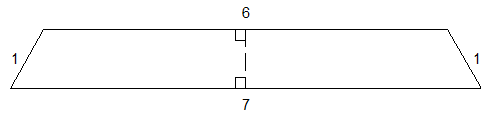
J'aurais dû préciser .
Vasimolo
#35 - 27-10-2016 17:20:46
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
Gâteau 1288
Ca ne change rien... Les bouts de ta figure sont à 60°, on y loge un triangle équilatéral.
D'ailleurs, elle peut facilement être ramenée à celle traitée pour le pentagone : (1;2) ou (6;7) c'est du pareil au même.
#36 - 27-10-2016 23:31:32
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 1128
Oui , je suivais plusieurs lièvres à la fois et j'ai clairement perdu le fil de ce que je faisais 
Je n'ai vraiment pas le temps ce soir mais il me semble qu'un triangle de côtés 2,n et n+1 s'écrase très vite et comme 2n+3 est impair ...
Affaire à suivre en tout cas .
Vasimolo
#37 - 27-10-2016 23:38:44
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Gââteau 128
Un triangle de côtés 2, n et n+1 inclus déjà un triangle de côtés 2, 1 et 1 dont on sait déjà qu'il contient un triangle de côtés 1, 1, 1...
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#38 - 28-10-2016 08:43:01
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
gâtzau 128
Une preuve ?
On place les sommets A et B de la plus longue diagonale sur une horizontale. Il y a 2 chemins pour rejoindre B depuis A en suivant le polygone. Par convention, on pose que le chemin le plus court passe sous AB.
On trace la ligne de crête du chemin court. La ligne de crête, c'est la courbe que décrit le sommet d'un triangle équilatéral dont la base glisse sur le chemin. Un point de crête, c'est le point de la ligne quand la base du triangle est confondue avec un segment.
On ne peut pas placer de triangle dans le polygone si le chemin long (au dessus de AB) passe intégralement sous la ligne de crête, ou si tous les points de crête sont en dehors du polygone.
1er cas)
Le chemin le plus court est confondu avec AB.
Le 1er segment en A du chemin long ne peut être incliné à plus de 60° avec AB, car sinon son point de crête serait à l'intérieur du polygone. Idem pour le dernier segment. Or on sait qu'un chemin long passe juste sur la ligne des crêtes: c'est la configuration du trapèze isocèle, avec chemin court à n segments et chemin long à n+1segments. Comme tout chemin passant sous la ligne est forcément plus court que le chemin de crête, le tracé du chemin long sous la ligne de crête est impossible.
2ème cas)
Le chemin court n'est pas confondu avec AB. Alors les points AB sont resserrés, la ligne de crête est plus proche de la ligne AB, le chemin long exige plus de détour. La contrainte pour faire passer le chemin long sous la ligne de crête est donc plus sévère, on ne peut pas davantage tracer ce chemin.
Il n'y a donc aucune configuration qui permette d'empêcher l'insertion d'un triangle dans le polygone à 2n+1 cotés.
#39 - 28-10-2016 19:39:39
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 1288
Je n'ai pas compris la preuve de Nodgim mais je suis convaincu que pour un nombre impair de côtés il y a toujours un triangle inscrit .
Peut-être parce-que le trapèze isocèle : n+1 , 1 , n , 1 , réalise l'aire minimale ?
Vasimolo
#40 - 28-10-2016 21:15:43
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
gâteay 128
C'est le triangle isocèle n, n, 1 qui réalise l'aire minimale.
#41 - 28-10-2016 23:36:55
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
fâteau 128
Oui , je vais arrêter de raconter des c... , et laisser reposer 
Vasimolo
#42 - 29-10-2016 17:31:44
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Gtâeau 128
De toute façon, la piste des aires pour établir la preuve me semble bien compromise. La forme trapèze a tout de même la particularité d'être la forme de plus faible largeur. Elle nous dit que si l'on voulait placer un triangle un chouia plus grand, il ne passerait pas (ni avec la forme triangle, du reste).
Sinon, Vasimolo (ou d'autres), où bloques tu dans la descrpition de ma preuve ?
C'est une preuve par l'absurde, où l'on s'efforce de ne jamais faire rentrer un triangle à l'intérieur du polygone.
#43 - 29-10-2016 19:58:54
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 182
Personnellement je n'ai rien compris , mais comme en ce moment je n'ai pas toute ma tête , je laisse les autres juger .
Vasimolo
|
 |

 Accueil
Accueil
 Forum
Forum








