 |
#1 - 03-09-2017 16:12:47
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
tourner en ronf (màj)
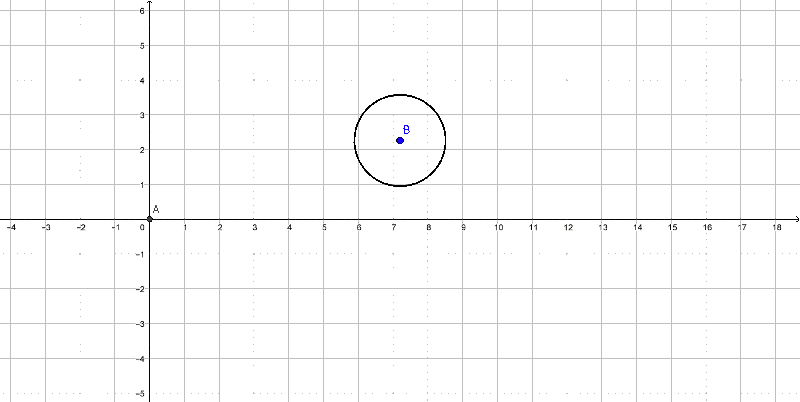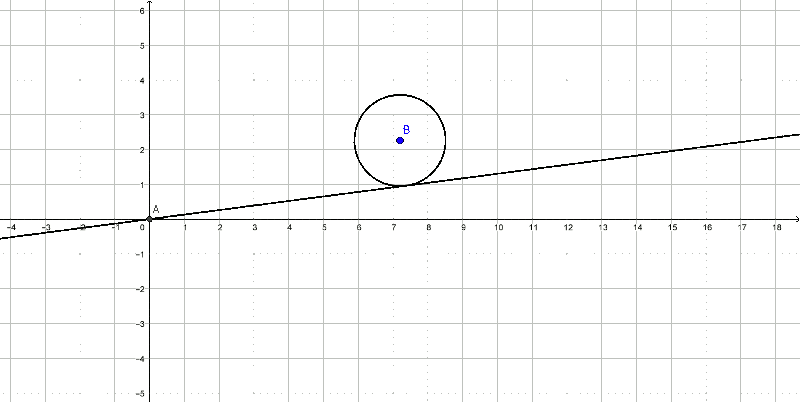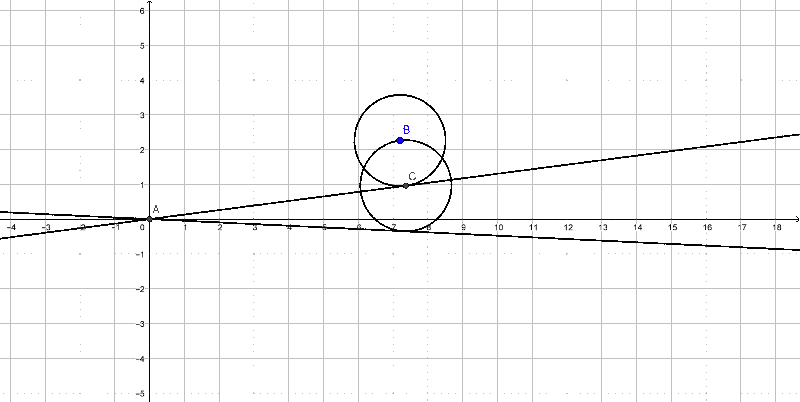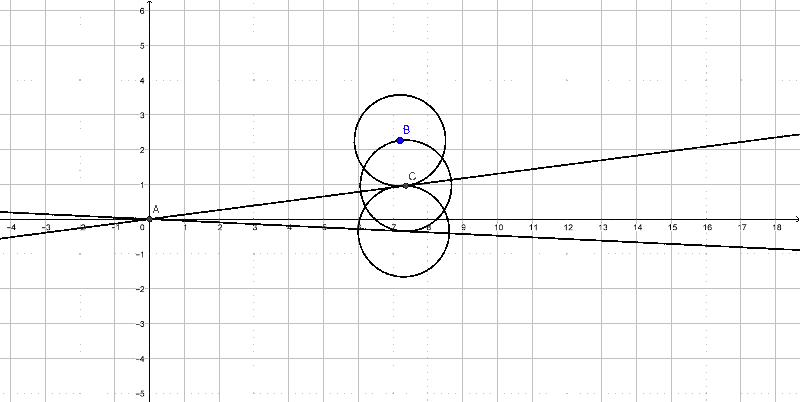
Soit C0 un cercle quelconque du plan.
On trace la tangente à C0 passant par l'origine. On trace un nouveau cercle, C1, de même rayon que C0 et de centre le point de tangence défini précédemment.
On itère le processus tant que possible et on construit ainsi une suite de cercles (Cn).
Combien d'éléments comporte la suite ?
#2 - 03-09-2017 19:33:50
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Turner en rond (MàJ)
On appelle R le rayon du cercle initial, et L la distance entre le centre de ce cercle et l'origine du repère.
On appelle (An) la suite des distances au carré entre les centres des cercles et l'origine du repère. On a donc A0 = L², et d'après le théorème de Pythagore, on a la relation de récurrence An+1 = An - R². La construction n'est plus possible dès lors que l'origine du repère est à l'intérieur du cercle, c'est-à-dire An < R² (si l'origine du repère est sur le cercle, on peut encore réaliser une étape, et le dernier cercle aura pour centre l'origine du repère).
La suite (An) est arithmétique. Le nombre de cercles tracés est donc E(L²/R²)+1.
#3 - 03-09-2017 21:26:32
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Tourner en rrond (MàJ)
Bonjour,
Soit d_n la distance du centre du cercle par rapport à l'origine
d_n+1^2 = d_n^2 - r^2
La suite s'arrete lorsque la distance d_n devient inférieure à r.
Le nombre d'élément est donc d_0^2/r^2 arrondi à l'excès
#4 - 04-09-2017 12:02:05
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3827
touener en rond (màj)
Si d est la distance entre l'origine et le centre du 1er cercle, et r le rayon du cercle, on peut tracer [(d/r)²] + 1 cercles, le dernier entourant le point origine.
#5 - 05-09-2017 19:18:59
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Toruner en rond (MàJ)
Bonsoir
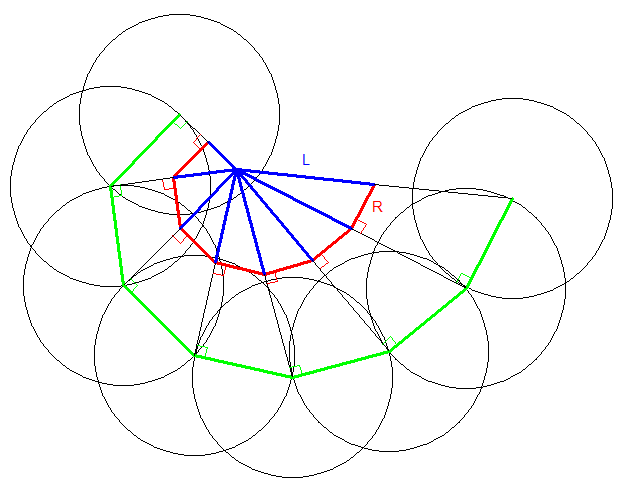
Ca fait penser à l'escargot de Pythagore . Si on note Ln la longueur des différents segments bleus ( L0 étant la longueur initiale ) , on a : L2n=L2−nR2 . Dès que le point A entre dans un cercle , l n'y a plus de tangente possible , on arrive donc ( sauf erreur ) à n=⌊LR⌋2 .
Vasimolo
#6 - 05-09-2017 20:14:23
- Spirou
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 494
Tourner en rond (MMàJ)
J'ai fais plusieurs pages de calculs, et je trouve comme résultat:
nombre d'éléments = arrondi a l'entier supérieur de (a² + b² - 1)
ou (a;b) est le centre du premier cercle.
J'ai trouvé ca en demontrant en premier qu'un cercle avait une tangente passant par l'origine si et seulement si la distance entre le centre du cercle et l'origine du repère était suérieure à 1. Ensuite j'ai trouvé que le la distance de l'oringine au n-ieme cercle était de a² + b² - n. Et je trouve finalement que lorsque n dépasse a² + b² - 1 la distance est inférieur à 1.
J'éspère ne pas m'etre trompé 
Spirou
#7 - 06-09-2017 18:37:59
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
Tourner en rond (MàJ))
Je vois que vous avez tous trouvé facilement !
Ce qui me donne envie de vous poser une autre question 
Le processus que j'ai décrit est en fait un algorithme de recherche : on s'en sert pour trouver quelque chose au voisinage d'un point en explorant la zone par cercles successifs.
Une stratégie intuitive consiste à appliquer l'algorithme en partant de 2 points équidistants du pôle, les 2 points et le pôle étant alignés :

Cette stratégie est-elle fiable ? (i.e existe-t-il des couples (L,R) pour lesquels des zones restent inexplorées ? Les caractériser ?)
#8 - 08-09-2017 21:53:42
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3234
- Lieu: Luxembourg
yourner en rond (màj)
Soient:
- R le rayon du premier cercle,
- D la distance entre l’origine et le centre de ce cercle,
- A l’angle entre la droite reliant l’origine au centre de ce cercle et la première tangente.
On aura: tanA = R/D
Si A/pi est irrationnel, alors la suite est infinie.
Si A/pi est rationnel, alors: k.m.2.pi.(A/pi) = k.n.2.pi <=> A/pi = n/m (fraction irréductible) et la suite sera finie et comportera m éléments.
#9 - 09-09-2017 03:32:48
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
Tourner en rond (àJ)
@Franky1103 : Ce n'est pas ça. La suite est toujours finie 
Concernant la 2ème question voici un exemple de couple qui ne marche pas :
(L=9.4,R=3)

#10 - 09-09-2017 10:29:12
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Touner en rond (MàJ)
Oui, en essayant avec Geogebra, pour certaines valeurs, il y a une zone proche du centre qui n'est pas recouverte. Juste, avant que j'essaie : as-tu une solution complète, ou poses-tu la question au cas où ?
#11 - 10-09-2017 16:16:42
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
tourner en rind (màj)
@Ebichu : J'ai quelques pistes mais pas de solution concrète malheureusement !
#12 - 10-09-2017 19:19:21
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3234
- Lieu: Luxembourg
Tournr en rond (MàJ)
Mince ! J'avais mal lu (et donc mal compris) l'énoncé: ça m'apprendra !
#13 - 10-09-2017 20:31:14
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Toourner en rond (MàJ)
J'ai eu un peu la flemme de me lancer dans les calculs, mais le plus simple me semble de prendre les calculs à l'envers, et de réduire le nombre de paramètres.
On partira donc d'un cercle de rayon r recouvrant l'origine (l = distance d centre à l'origine < r ) , et on construira les suivants tangents à la droite passant par l'origine et le centre du dernier cercle.
La réponse sera évidemment la même si le rapport r/l est le même. On peut donc fixer la valeur de l à 1. De plus, le problème est invariant par rotation, on peut donc considérer le centre du premier cercle sur l'axe des abscisses.
On peut alors conjecturer qu'à partir de (Edit: j'avais mal modélisé) r = 1.18 environ, il n'y a plus de vide (on peut calculer cette valeur mais je ne l'ai pas fait)
Il faut alors démontrer que lorsque l'on est suffisamment éloigné de l'origine, il n'y a plus de vide, puis trouver le moyen de calculer de manière pratique le résultat à partir du couple L,R selon la définition de Sydre. (Il faut donc trouver le terme général de la suite pour trouver le cercle final, et pouvoir regarder le rapport r/l)
Bon, c'est plus facile à dire qu'à faire...
Edit:
Je viens de m’apercevoir que lorsque le rapport r/l dépasse 21.29 (environ) , on a à nouveau un trou dans notre figure...
#14 - 11-09-2017 13:13:48
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
tourner en rind (màj)
@caduk : Oui, la présence de trous n'est pas restreinte à un intervalle unique ...
Pour l'instant je conjecture qu'il y a des trous si :
q2⌊q2⌋+1≥f(q)
Avec q=LR et f(q) proche de 1.
#15 - 11-09-2017 15:20:09
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Tourner en rond (àJ)
Oui, mais au delà de cet valeur, ça se stabilise, le trou reste toujours...
Edit:
Il y a un trou jusqu'à 1.63 environ
Je pense qu'après, il n'y a plus de trou que l'on n'a pas vu.
Il y aurait donc absence de trou sur l'intervalle [1.63,21.29]
#16 - 12-09-2017 08:40:10
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3827
tourner en rond (màh)
Je m'étais un jour amusé à calculer la largeur entre 2 spires consécutives de cette spirale, et je crois me souvenir que ça devait être quelque chose comme PI quand R grandit.
#17 - 12-09-2017 09:38:11
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3827
tourner eb rond (màj)
Je le confirme, le calcul n'est pas compliqué. Pour s'en convaincre, avec un petit tableur, on voit que pour r=1 et d= 100, d = 103,13...après une somme d'angles de 6,28 (2 PI = 1 tour).
#18 - 12-09-2017 13:34:43
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3827
rourner en rond (màj)
Et donc, pour en venir à ta stratégie de 2 spirales emboitées, ça marche. mais seulement à partir de quelques tours. En effet, les trous sont à une distance min V3/2 d'une spirale, c'est à dire à plus que la moitié de P1/2.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum










