 |
#26 - 15-03-2018 23:01:19
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Les aventuriers du tthéorème perdu (partie 2)
Une idée en l'air avant de me coucher :
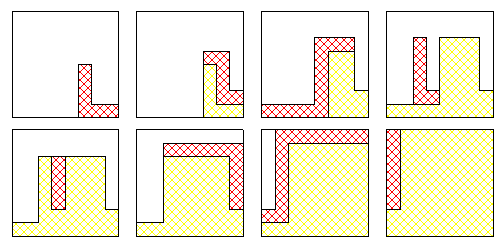
On empile les serpents de haut en bas , k serpents ne peuvent pas remplir plus de k lignes .
Après il faut justifier 
Vasimolo
#27 - 16-03-2018 07:45:54
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
Les aventuriers du théorème perdu (partiee 2)
Ce n'est pas mal du tout !
Soit tu remplis 1 ligne du bas et dans ce cas au mieux une seule colonne au dessus de cette ligne. Soit tu remplis 1 ligne en haut mais seulement 1 colonne de la partie basse.
#28 - 16-03-2018 14:51:52
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Les avnturiers du théorème perdu (partie 2)
Un petit complément : on peut ranger les serpents selon une relation d'ordre total ( pas forcément unique ) : complétant "est en dessous de" . Un serpent est en dessous d'un autre s'il a une case en dessous sur une même ligne verticale .
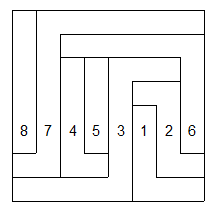
ici : 1<2<3<4<5<6<7<8.
Il n'y a plus qu'à voir que k serpents ne peuvent pas recouvrir plus de k lignes .
Vasimolo
#29 - 16-03-2018 16:21:46
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
Les aventuriers u théorème perdu (partie 2)
Le problème est toutefois celui ci : un serpent peut toujours remplir n colonnes (de l'extrême droite à l'extrême gauche) plus un certain nombre de cases supplémentaires montantes, ce qui autorise à penser que moins de n serpents peuvent remplir le casier.
#30 - 16-03-2018 16:40:31
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Les aventuriers du théorème pedu (partie 2)
C'est vrai qu'il faudrait préciser un peu mais l'idée est que le serpent de rang k ne peut pas remplir complètement la ligne k+1 .
Vasimolo
#31 - 17-03-2018 08:18:18
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
les aventuriers du yhéorème perdu (partie 2)
Euh, si. Même le n° 1 peut occuper entièrement la ligne 2.
#32 - 17-03-2018 09:05:02
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Les aventuriers du théorème perdu (partie 2))
Non car si le premier serpent occupait complètement la ligne 2 , il serait au dessus d'un autre serpent et aurait donc usurper son numéro .
Vasimolo
#33 - 17-03-2018 11:12:28
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
led aventuriers du théorème perdu (partie 2)
Bonne réponse Vasimolo. Du coup, ta proposition me plait de plus en plus.
Avec ta méthode il est impossible de placer un serpent "en escalier" tant qu'on n'a pas placé tous ceux qui se trouvent en dessous de lui. Autrement dit, la contribution de chaque serpent au dessus d'une ligne donnée ne peut être que sa partie verticale, soit 1 seule colonne par ligne. Les parties horizontales des serpents en escalier ne sont là donc que pour finir une ligne. Donc il est impossible qu'une ligne soit remplie en avance des lignes à occuper puisque k lignes occupées ne peuvent remplir au mieux que k colonnes d'une ligne supérieure.
On tient la solution là non ?
#34 - 17-03-2018 11:48:22
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Les avenuriers du théorème perdu (partie 2)
C'était en effet mon idée , j'étais en train de vérifier qu'on pouvait toujours classer les serpents et ça y est je suis convaincu ( le classement est rarement unique mais il existe toujours ) .
J'ai encore d'autres choses à vérifier ( désolé je suis très lent ) .
Merci pour le décryptage de mes messages pas toujours très clairs 
En attendant l'avis d'Ebichu 
Vasimolo
#35 - 17-03-2018 16:08:02
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
les acenturiers du théorème perdu (partie 2)
Il faut tout de même que tu prouves l'existence d'un serpent "en dessous de tous les autres " à chaque étape de la construction. C'est assez court mais c'est ta démo je te laisse faire.
#36 - 17-03-2018 17:35:37
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Les aventuriers du théorème perdu (partie 22)
En fait il faut prouver que la relation "est en dessous de" peut être prolongée en un ordre total ( j'en parlais dans un message précédent ) . Ça semble presque évident car si on a a<b et b<c on ne peut pas avoir c<a : ajouter que a<c peut-il créer un conflit ?
Vasimolo
#37 - 17-03-2018 17:48:48
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Les vaenturiers du théorème perdu (partie 2)
Concernant la première partie de ta preuve, chapeau, c'est très joli  Je suis convaincu. Ce n'est effectivement pas très facile à rédiger, ça demande encore un peu de travail, mais je pense qu'il sera possible de s'en sortir. Je suis convaincu. Ce n'est effectivement pas très facile à rédiger, ça demande encore un peu de travail, mais je pense qu'il sera possible de s'en sortir.
Par contre, je ne saisis pas bien la fin de l'argument. Peux-tu préciser un peu les grandes lignes de "Il n'y a plus qu'à voir que k serpents ne peuvent pas recouvrir plus de k lignes" ?
#38 - 17-03-2018 18:00:24
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Les aventuriers du théorème perdu (partiee 2)
La formulation n'est pas terrible , j'aurais du dire "les k premiers serpents ne peuvent pas couvrir les k+1 premières lignes" . Nodgim a donné un argument qu'il faudrait étayer .
Vasimolo
#39 - 18-03-2018 11:11:25
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Les aevnturiers du théorème perdu (partie 2)
Je crois avoir quelque chose de plus complet .
Il est clair que le serpent 1 ne peut pas occuper plus d'une case de la ligne 2 sinon il y aurait une case vide sous au moins une de ces deux cases et le serpent 1 serait mal nommé . Supposons par récurrence qu’au plus k cases de la ligne k+1 sont occupées par les k premiers serpents et considérons les cases de la ligne k+2 . Au plus k cases sont occupées par les k premiers serpents sinon il y aurait un trou sous l'une de ces cases dans la ligne k+1 . Notons x le nombre de cases occupées de la ligne k+2 et ajoutons le serpent k+1 . Toujours pour la même raison ce serpent ne peut pas occuper plus de k+1-x cases ( le +1 pour la case de la ligne k+1 qui hisse le serpent sur la ligne k+2 ) donc un maximum de k+1 cases occupées pour l'ensemble de la ligne.
PS : il peut y avoir plusieurs cases du serpent k+1 sur la ligne k+1 mais une seule peut-être surmontée par une case occupée de la ligne k+2 .
J'espère ne pas m'être trop emmêler dans les indices 
Vasimolo
#40 - 18-03-2018 11:33:23
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
les avznturiers du théorème perdu (partie 2)
#41 - 18-03-2018 12:21:39
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Les aventuriers du théorème peerdu (partie 2)
Avant de valider, j'ai besoin d'un éclaircissement. Je veux être sûr d'avoir bien compris.
Notons x le nombre de cases occupées de la ligne k+2
Je suppose qu'il faut comprendre "le nombre de cases de la ligne k+2 occupées par les k premiers serpents" ?
Dans ce cas, on a x<=k. Mais quand, par la suite, tu dis :
ce serpent ne peut pas occuper plus de k+1-x cases
ce ne serait pas plutôt "ce serpent ne peut pas occuper plus de x+1 cases" ? Ce qui ne change pas la conclusion, car x<=k donc x+1<=k+1.
#42 - 18-03-2018 12:42:39
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Les aventuriers du théorème perduu (partie 2)
Pour la première remarque : oui , mais pour la deuxième : non , il me semble que les paramètres sont bons .
Vasimolo
#43 - 18-03-2018 13:04:06
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Les aventurriers du théorème perdu (partie 2)
OK, erreur de raisonnement de ma part, j'ai compris maintenant. C'est une belle démonstration, bravo ! Sur un sujet vraiment beaucoup plus difficile qu'il en a l'air.
Ma preuve était très différente de la tienne, on peut même dire qu'elles n'ont rien à voir. Si ce n'est un point commun : je pense qu'il faudrait un certain boulot pour les amener à passer le cap d'un assistant de preuve...
#44 - 18-03-2018 16:32:12
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
Les aventuriers du théorème perdu p(artie 2)
Quelle que soit ta solution, Ebichu, il a dû te falloir beaucoup d'opiniâtreté pour arriver à la trouver. Ceux à qui on propose une énigme dont on a nous mêmes trouvé une solution ont l'avantage de savoir qu'il en existe une, il y a une stimulation naturelle.
#45 - 18-03-2018 16:33:36
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
les aventurierq du théorème perdu (partie 2)
Vasimolo a écrit:En fait il faut prouver que la relation "est en dessous de" peut être prolongée en un ordre total ( j'en parlais dans un message précédent ) . Ça semble presque évident car si on a a<b et b<c on ne peut pas avoir c<a : ajouter que a<c peut-il créer un conflit ?
Vasimolo
Certes, non, mais dit comme ça, il y a un goût d'inachevé. Enfin, pour moi en tout cas.
#46 - 18-03-2018 17:43:19
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Les aventuriers du théorème prdu (partie 2)
@Ebichu et Nodgim
Il est certain que la preuve n'est pas finie même si je suis quasiment sûr qu'elle peut être complétée , j'essaierai de la rédiger entièrement dans quelque temps ( à moins que quelqu'un d'autre s'en charge avant ) . En attendant j'aimerais bien qu'Ebichu nous donne l'idée de sa démonstration pour voir quels leviers il a utilisé . D'autre part j'avais proposé à Ebichu en privé de partager son problème avec d'autres sites , il m'avait demandé d'attendre un peu pour des raisons auxquelles j'adhère complètement : qu'il me fasse signe quand cela sera possible .
Pour finir , quelques remarques en vrac sur ce problème :
Il entre d'emblée dans la catégorie de ceux que j'affectionne : le problème est compréhensible par un gamin de maternelle et les outils de résolution peuvent être pioché dans toute la boîte à outils des mathématiques sans qu'aucun ne soit privilégié à priori .
On peut remplir le carré avec un seul serpent s'il peut aller librement à gauche ou à droite : que perd-on en limitant les déplacements d'un seul côté ? Initialement j'étais parti sur la distance Manhattan car le nombre de cases du serpent est exactement la distance entre les extrémités ( c'est faux pour un serpent gauche-droite ) mais je n'ai rien trouvé de convaincant . C'est alors que j'ai pensé à la relation "est au dessus de" qui n'existe plus pour les serpents gauche-droite , après il faut laisser mûrir .
J'ai arrêté mes petites études en mathématiques depuis très longtemps : une relation d'ordre partiel ( sur un ensemble fini ) peut-elle toujours être complétée en un ordre total ?
J'ai encore d'autres questions/remarques mais je vais attendre les réponses 
Vasimolo
#47 - 18-03-2018 18:55:51
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Les aventuriers du théorème prdu (partie 2)
@nodgim : tu appelles cela de l'opiniâtreté, j'appelle cela de la folie furieuse. Je ne pensais qu'à ça en m'endormant pendant deux mois. Je ne sais pas s'il faut encourager ce genre de comportement. Ça aurait été plus efficace d'en discuter avec d'autres personnes dès le début, mais des fois on se lance un défi... Je suis d'accord avec ton analyse, c'est sans doute moins décourageant quand on sait qu'il existe une solution, mais ça n'enlève rien à la performance de Vasimolo.
Pour le problème auquel tu fais allusion, je pense voir les arguments qui permettent de conclure, ça utilise des résultats de topologie qu'il n'est sans doute pas facile de rédiger proprement.
@Vasimolo : tu peux envoyer le problème sur d'autres sites.
Voici ma démo : http://www.prise2tete.fr/upload/Ebichu-serpents.pdf
Et pour la suite : https://fr.wikipedia.org/wiki/Th%C3%A9o … _Szpilrajn
#48 - 18-03-2018 19:18:53
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Les aventurieers du théorème perdu (partie 2)
@Ebichu
Je vais lire ça en détail ( il y a de quoi faire ) 
Pour l'addiction aux problèmes , je connais , c'est la raison pour laquelle je ne participe plus de près ou de loin à tout ce qui concerne la conjecture de Syracuse .
Vasimolo
#49 - 18-03-2018 20:13:08
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Les aventurirs du théorème perdu (partie 2)
Je crois que si on allait expliquer ça aux alcooliques anonymes ils nous regarderaient bizarre.
#50 - 21-03-2018 08:02:52
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
Les aventurierrs du théorème perdu (partie 2)
J'ai lu ta preuve par transformation, sans toutefois l'avoir analysée à fond pour dire si elle est valide ou pas. C'est une piste que j'avais explorée sans aller au bout, précisément à cause de la multiplicité des cas.
Travail stakanoviste payant au final.
|
 |

 Accueil
Accueil
 Forum
Forum








