 |
#1 - 26-02-2018 21:33:58
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
les aventuriers du théorème peedu (partie 2)
Voici la deuxième partie des aventures de New-Jersey Smith, autant ne pas perdre de temps, car il risque de vous occuper un moment.
Nous avions laissé New-Jersey en fâcheuse posture, une myriade de serpents se dirigeant vers lui. Cependant, il s'avère d'une part que New-Jersey n'est pas une souris, et d'autre part, qu'il n'a pas bon goût. C'est donc en toute logique que les serpents se désintéressent de lui et retournent vaquer à leurs occupations. Braves bêtes.
New-Jersey a donc tout son temps pour faire une observation mathématiques intéressante : les serpents, de tailles entières et non nulles, peuvent être regroupés en deux familles.

Ceux en rouge sur le schéma se dirigent exclusivement vers le nord ou l'ouest (ou alors, vers le sud ou l'est). Ceux en bleu se dirigent exclusivement vers le nord ou l'est (ou alors, vers le sud ou l'ouest). Saurez-vous démontrer, comme la dernière fois, qu'il faut au moins N serpents pour recouvrir une pièce de taille NxN ?
Je ne cache pas les réponses des participants : je ne peux pas mettre plus de 999 heures, et il m'en a fallu plus pour trouver la réponse...
#2 - 27-02-2018 19:29:10
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,044E+3
Les aventuriers du théoèrme perdu (partie 2)
Salut, 
Un essai assez simpliste, mais pas que...
On peut toujours imaginer que les serpents ne se déplacent que vers la droiteuniquement, cela ne change rien au problème.
Le coin haut-gauche doit être recouvert. S'il l'est par un serpent se déplaçant vers le haut, on se ramène dans le pire des cas à traiter le cas N-1 avec un serpent de moins. Par récurrence, dans cette hypothèse, il faudra 8 serpents au minimum.
Idem si le serpent se déplace vers le bas mais ne tourne qu'à la dernière colonne.
Idem, s'il ne tourne pas du tout.
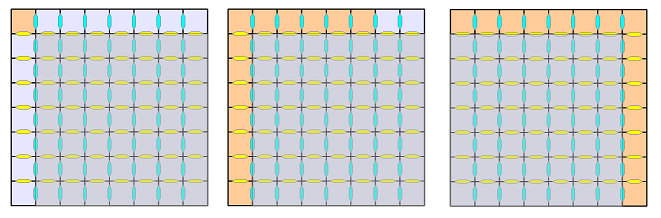
Dans le cas ou ce serpent se déplace vers le bas, quelle que soit sa forme, on peut ramener la situation au cas de 2 carrés de dimension X et Y avec X+Y = N-1 en prenant comme base le point ou le serpent coupe la diagonale.
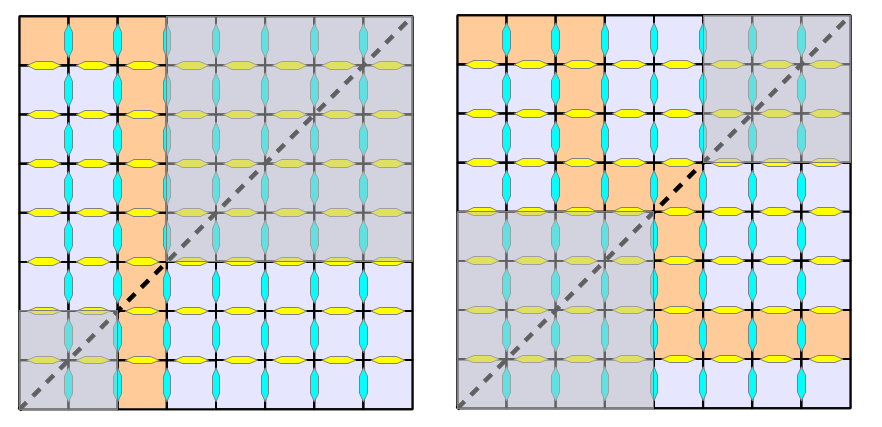
Toujours par récurrence, et sachant qu'un carré de 1 case nécessite un serpent, on conclut.
#3 - 27-02-2018 19:31:24
- LeJeu
- Passionné de Prise2Tete
- Enigmes résolues : 25
- Messages : 78
Les avenutriers du théorème perdu (partie 2)
[Edit] Une contribution non pertinente que j'efface donc
#4 - 27-02-2018 19:53:31
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Les aventuriers du théoème perdu (partie 2)
@gwen27 : beaucoup de bonnes idées dans ton message. Un problème cependant : et si ton serpent orange est trop court, et ne touche ni le bord d'en bas, ni celui de droite ? Il y a alors la possibilité qu'un même serpent, passant par l'espace laissé en bas à droite, recouvre les carrés X et Y...
#5 - 27-02-2018 20:21:38
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,044E+3
les aventuriers du théotème perdu (partie 2)
Oui, mais il ne remplira pas les vides que je n'ai pas grisés dans ce cas, les points de rebroussement, si on peut les appeler comme ça, une case à chaque tournant. Un serpent touchant ces deux carrés me ramène à la réduction du premier dessin que l'on traite au préalable.
#6 - 27-02-2018 21:11:35
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Les aventuriers du théorème pedu (partie 2)
Heu, je ne comprends pas ce dernier message ?
#7 - 27-02-2018 21:59:08
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Les aventuriers du théorèmee perdu (partie 2)
J'ai vu ta mise à jour, mais je ne suis toujours pas convaincu. Sur un exemple :
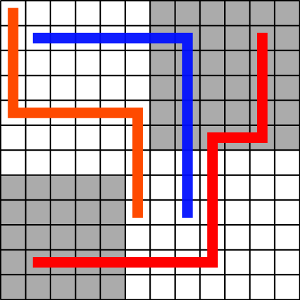
S'il y a sur la grille un serpent comme le orange, on en déduit les deux carrés gris. Mais comme le serpent orange ne touche pas les bords, on peut imaginer un serpent fourbe, comme le rouge, qui va toucher les deux carrés. Quant aux cases blanches, elles pourraient être recouvertes par des serpents qui, comme le bleu, servent par ailleurs à recouvrir les deux carrés gris.
#8 - 27-02-2018 22:46:31
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Les aventuriers ddu théorème perdu (partie 2)
On suit bien la solution de Gwen et intuitivement on ne va pas réussir à joindre toutes les zones bleues aux grises sans un rebroussement contraire à la nature des serpents mais il manque un argument .
Il faudrait aussi évoquer le cas où le serpent issu du coin supérieur gauche ne traverse pas la diagonale ( même si c'est évident ) .
Vasimolo
#9 - 28-02-2018 08:40:30
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Les aventuriers du théorèm eperdu (partie 2)
@Vasimolo : on retrouve une situation similaire à celle de ton problème... on voit bien que ça doit marcher, mais comment le montrer proprement ?
Il faudrait aussi évoquer le cas où le serpent issu du coin supérieur gauche ne traverse pas la diagonale ( même si c'est évident )
Je ne trouve pas cela évident : comment règlerais-tu ce cas ?
#10 - 28-02-2018 08:53:06
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
les aventuriers du théotème perdu (partie 2)
Une autre piste peut être.
Tout d'abord, on remplace les cases par des points et donc chaque point est relié par une liaison en extrémité ou en passage (représentation type graphe)
Pour un graphe donné, on va s'efforcer de remplacer, ligne par ligne, en commençant par exemple par celle du bas et en montant ligne par ligne, chaque segment vertical par un horizontal. Comme, pour une ligne donnée, une liaison n'a au mieux qu'une seule verticale, cette substitution se fait normalement avec un nombre inchangé de liaisons, car on raccourcit toujours une liaison par grignotage de l'extrémité de sa partie verticale, ou avec un nombre moindre par regroupement de 2 liaisons horizontales.
Au final, avec seulement des liaisons horizontales, il y a au minimum n liaisons.
#11 - 28-02-2018 09:46:53
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Les aventuriers du héorème perdu (partie 2)
Bon il faut tout de même affiner, car déjà on ne tombe par toujours sur une extrémité verticale, comme dans le cas d'une liaison horizontale puis coudée vers le haut. La coupe d'une telle liaison doit se faire en groupant 2 autres liaisons en une seule pour ne pas augmenter le total de liaisons.
Pas encore au point tout ça....
#12 - 28-02-2018 09:58:46
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
les aventuriers du tjéorème perdu (partie 2)
Non , le cas où la diagonale n'est pas traversée n'est pas plus clair que le reste 
Ce qui marche à coup sûr c'est que si on trouve un serpent qui relie deux bords on peut conclure par récurrence . Je pense qu'on est toujours dans cette situation s'il y a au plus n serpents , mais il faut le prouver .
Vasimolo
#13 - 28-02-2018 10:23:43
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
les aventuriers du théorème perdu (oartie 2)
@Vasimolo : avec une grille 4x4, place 4 serpents qui sont des tétraminos L de façon à former une espèce de croix gammée => contre-exemple.
#14 - 28-02-2018 10:28:17
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Les aventuriers du téorème perdu (partie 2)
En effet , il faut trouver une autre idée 
Vasimolo
#15 - 28-02-2018 11:00:19
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,044E+3
les aventuriers du théorème perdu (partir 2)
Une autre manière de voir les choses est de compter les points de départ (de gauche à droite).
Si il y en a N dans la première colonne, c'est trivial.
S'il en manque 1, il doit être comblé, soit par un nouveau départ, soit par un autre serpent "indéterminé" immédiatement voisin qui choisit donc entre haut et bas.
Le "vide" est juste décalé à la colonne suivante et le premier serpent ne pourra plus le combler. On peut toujours le combler par un nouveau départ...
Quoiqu'il en soit, on arrive à N départs:
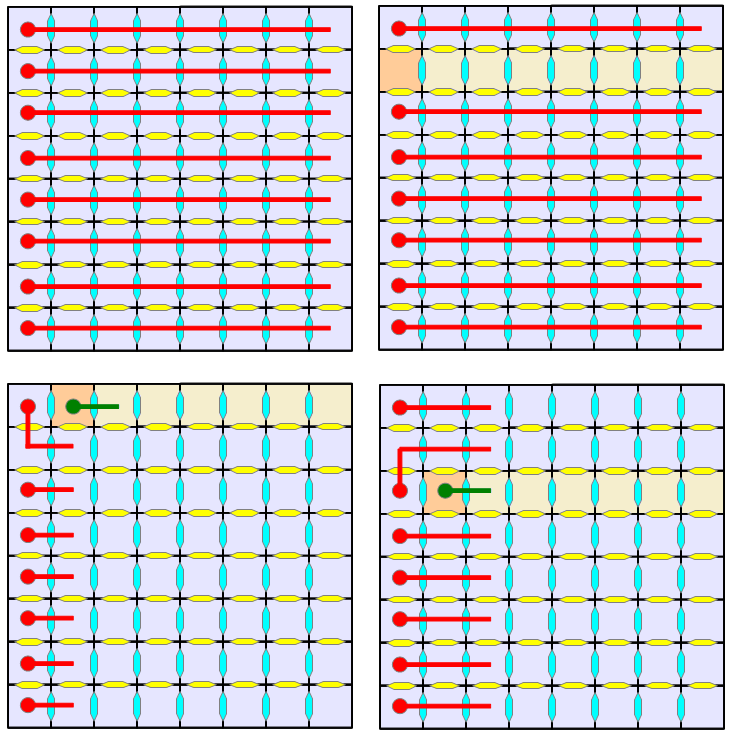
On peut aussi continuer à combler ce vide avec d'autres serpents, jusqu'au dernier indéterminé, ce qui peut se faire plus ou moins tard, mais au final, seulement N-1 fois maximum. Au pire, à la dernière colonne, il faudra un nouveau départ, voire avant.
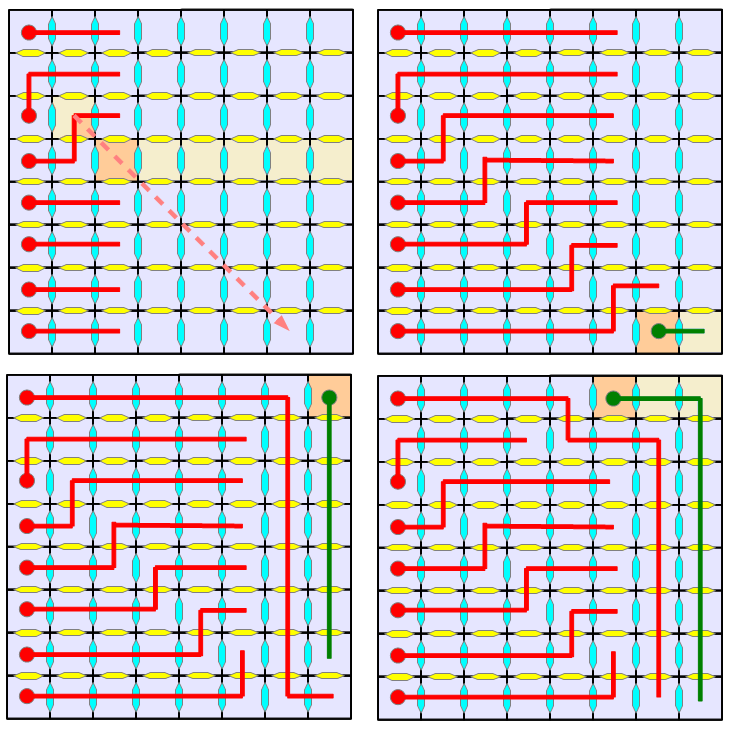
Imaginer 2 départs en moins, ou même N-1 dés le début n'y change rien, il faut un nouveau départ pour combler un vide.
#16 - 28-02-2018 11:23:29
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Les aventuries du théorème perdu (partie 2)
J'ai l'impression que tu raisonnes à l'envers 
Tu pars d'une configuration très particulière à 8 serpents que tu déformes progressivement en expliquant pourquoi on ne peut pas la réduire . Et pourquoi n'existerait-il pas une configuration avec 7 serpents n'aboutissant pas à ton point de départ ?
Vasimolo
#17 - 28-02-2018 11:32:08
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,044E+3
Les aventurierss du théorème perdu (partie 2)
Pas vraiment, je pars de 7 serpents, mais j'aurais pu mettre le vide ailleurs, ou partir de 1 ou 2 serpents seulement ... Il y a obligatoirement au moins 1 départ en colonne 1. Après, le nombre de vides augmente, c'est tout, le raisonnement ne change pas..
#18 - 28-02-2018 12:00:01
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
les aventuriers du théorème perdu (oartie 2)
@Gwen : J'ai pu passer à côté de ton idée mais tu pars d'un recouvrement avec n serpents qu'on ne peut pas réduire et tu en déduis qu'on ne peux pas faire avec moins de n serpents .
Pour moi il y a un problème logique .
Vasimolo
#19 - 28-02-2018 12:24:15
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,044E+3
Les aventuriers du théorème perddu (partie 2)
Non, je pars avec un recouvrement supposé de moins de N serpents dont un au moins débute en colonne 1, et j'aboutis à la conclusion que je suis obligé d'en rajouter. 
#20 - 28-02-2018 14:42:19
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
les aventuriers du théprème perdu (partie 2)
@gwen27 : je vois bien l'idée, j'avais eu la même à l'époque. Cependant, pour l'instant, ta preuve est bien informelle. Il faudrait écrire tout ça un peu plus proprement.
Je n'ai jamais réussi à la formaliser : j'avais essayé de trouver un invariant en utilisant le nombre de départs, ou de vides, ou de serpents allant dans un sens ou l'autre... mais je n'ai pas trouvé.
Bref, pour l'instant, ce n'est pas assez clair pour que je sois convaincu. Mais il ne manque peut-être pas grand chose pour que ce soit le cas.
#21 - 11-03-2018 12:53:47
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
les aventuriers du théorème oerdu (partie 2)
Le problème mérite bien un petit "up" , non ?
Vasimolo
#22 - 11-03-2018 19:26:09
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Les aventuriers du théoèrme perdu (partie 2)
C'est fait. Ce n'est pas parce qu'il n'y a pas de réponse qu'il n'y a pas de recherche.
" Il n'est pas nécessaire de réussir pour persévérer "
Une piste m'a mené sur un autre problème. Il s'agit d'un damier de n lignes et une infinité de colonnes, qu'on remplit évidemment avec n serpents en ligne. Mais si 1 seul d'entre eux se met à prendre une verticale, fusse sur une seule case, c'en est fini du remplissage infini si on ne veut ignorer aucune case d'aucune colonne. Le but est alors de savoir combien de colonnes après le coude on peut encore remplir. Pour un seul serpent déviationniste, c'est facile, mais à partir de 3, ça commence à se compliquer....
#23 - 12-03-2018 18:24:06
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Les aventuriers du théorème perud (partie 2)
Je sais bien qu'il y en a qui cherchent , la remontée était destinée à ceux qui n'avaient pas vu le problème ou le croyaient résolu 
Personnellement j'étais parti sur une autre variante plus simple que celle d'Ebichu et qui peut être un point de départ pour le cas général :
On considère un unique serpent autorisé à se déplacer dans les quatre directions et occupant toutes les cases du carré . On peut couper ce serpent en morceaux bleus et rouges : pourquoi le nombre de morceaux est-il au moins égal au côté du carré ?
Vasimolo
#24 - 12-03-2018 21:45:18
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Les aventuriers du théorème perdu (paartie 2)
Je ne réagis pas car je ne veux pas parasiter le cours de votre pensée qui vous entrainera peut être vers d'autres territoires que la mienne, mais je suis votre progression avec intérêt.
#25 - 13-03-2018 08:33:00
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Les aventuriers du théorème perdu (parrtie 2)
Vasimolo a écrit:On considère un unique serpent autorisé à se déplacer dans les quatre directions et occupant toutes les cases du carré . On peut couper ce serpent en morceaux bleus et rouges : pourquoi le nombre de morceaux est-il au moins égal au côté du carré ?
Vasimolo
Suis également passé par cette hypothèse (en fait le serpent est un chemin qui relie n² sommets avec n(n-1) liaisons. En ôtant moins de n-1 liaisons, peut on atteindre tous les sommets ? )
|
 |

 Accueil
Accueil
 Forum
Forum












