 |
#1 - 04-12-2018 15:02:10
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
La découpe du parallélogrammme
Un collègue de retour de voyage d'affaires de Chine m'a ramené ça, connaissant mon goût pour les casse tête. Sympa le cadeau chinois 😂.
(Pour augmenter la pression, c'est un concours de collégiens surdoués; le meilleur aurait trouvé la réponse en moins d'une minute). J'ai pensé à vous.
Le sujet:
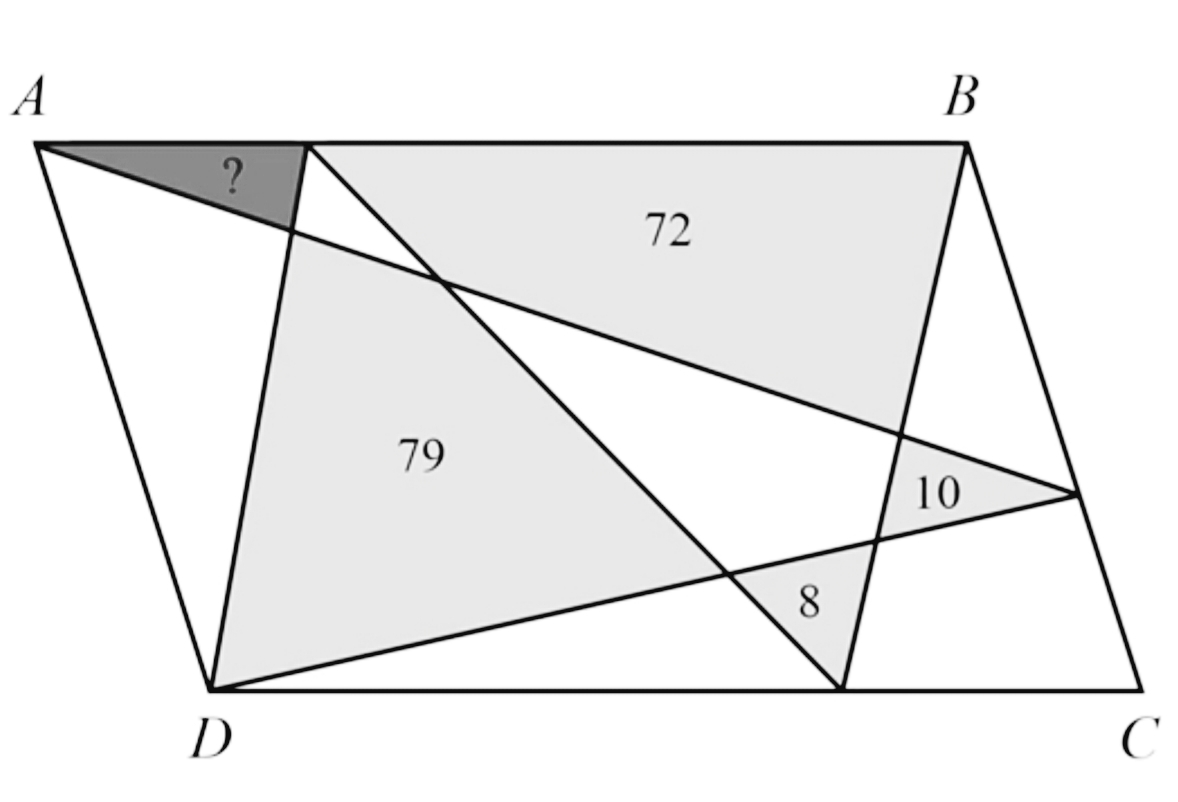
ABCD est un parallélogramme. Les aires des parties grises claires sont données. Trouvez l'aire de la partie grise foncée?
Bonne chance
(72h)
#2 - 04-12-2018 17:32:42
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
La découpe du parallélogrmame
Bonjour,
Spoiler : [Afficher le message] 9, qui valide 
#3 - 04-12-2018 19:30:11
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,998E+3
la découpe du parallélogtamme
C'est effectivement assez trivial.
79 + 10 + deux zones blanches font la moitié de la surface.
72 + 8 + les mêmes zones blanches + la zone gris foncé aussi.
Donc : 9
#4 - 04-12-2018 21:46:31
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
la découpe du paralmélogramme
Salut,
il suffit de remarquer que l'aire du triangle qui a la pointe à droite vaut la moitié de l'aire du parallélogramme, tout comme la somme des aires des deux triangles qui ont la pointe en bas.
Donc 79+10+aire(2 morceaux blancs)=72+8+aire(2 morceaux blancs)+?.
Donc ?=9.
#5 - 04-12-2018 23:09:17
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
La découpe du parallléogramme
Et bien, trop facile par ici comme je l'imaginais 
2 réponses argumentées, bravo, et 1 réponse issue visiblement d'un abus de la case de validation 
#6 - 05-12-2018 06:43:24
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
La découpe du paralélogramme
kossi_tg #5 a écrit:2 réponses argumentées, bravo, et 1 réponse issue visiblement d'un abus de la case de validation
Vu le nombre de réponses qui précèdent, j'en déduis que c'est moi qui suis accusé d'abus.
Eh bien non, absolument pas, la case réponse ne m'a servi que pour vérifier mon résultat !
S'il y avait eu des lettres à toutes les intersections de la figure, j'aurais détaillé, mais là j'avoue avoir eu la flemme…
#7 - 05-12-2018 13:18:07
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
la découpe du parzllélogramme
x + 72 + 8 = 79 + 10 => x = 9
#8 - 05-12-2018 15:12:18
la découpe du paramlélogramme
Les droites internes sont elles quelconques?
#9 - 05-12-2018 22:30:39
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
ka découpe du parallélogramme
#10 - 06-12-2018 19:00:31
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
la fécoupe du parallélogramme
Bonjour 
J'avais cherché des choses compliquées mais c'est très simple quand on a vu l'astuce . L'aire des deux triangles reposant sur la base inférieure est égale à l'aire des deux triangles s'appuyant sur la base supérieures . On fait de même à droite et à gauche et tout se simplifie miraculeusement : x=9 .
Très joli problème !!!
En moins d'une minute je dis bravo , il m'a fallu quelques heures 
Vasimolo
#11 - 08-12-2018 23:27:37
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
la découpe du parallélogrzmme
Eric a écrit:Les droites internes sont elles quelconques?
Les droites sont celles qui permettent d'avoir les aires données, sans qu'on ait d'infos supplémentaires.
#12 - 08-12-2018 23:36:17
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
aL découpe du parallélogramme
Merci à tous.
L'astuce est déjà donné. Il faut en effet exploiter la propriété suivante des triangles. Si ABC est un triangle alors il a la même aire que tout autre triangle ABM, pour tout M sur la droite parallèle à (AB) passant par C. [en d'autre terme, (CM)//(AB)]
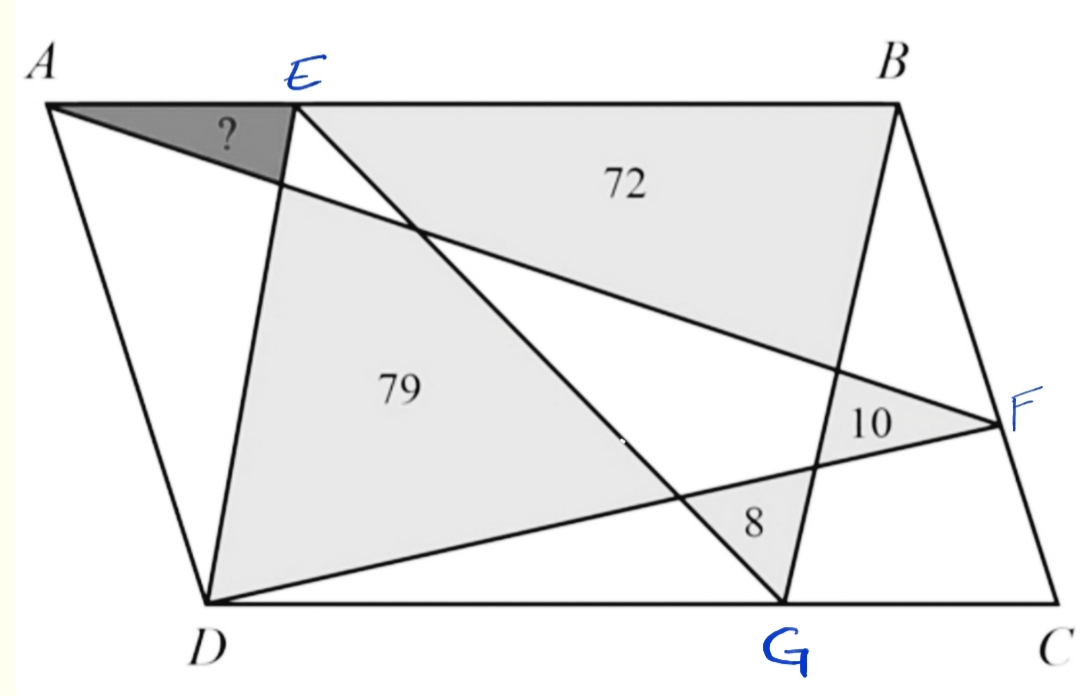
* ADB et ADF ont la même aire, c'est à dire la moitié de ABCD
* EBG et EBD ont la même aire
* aire EBD + aire AED = moitié aire ABCD = aire ADF
On en déduit que ? = 9
Voilà
#13 - 09-12-2018 15:48:57
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
la découpe su parallélogramme
Trouver, à partir des données, l'aire de la partie gris foncé était facile, mais il me semble que les valeurs de ces données ne sont pas cohérentes.
Les rapports des aires des parties internes ne dépendent ni des longueurs des côtés du parallélogramme, ni du décalage horizontal des côtés haut et bas.
Ces rapports ne dépendent que de la position relative de E sur AB, et de F sur CB (notations de kossi_tg #12).
Je n'ai pas réussi à ajuster ces 2 paramètres, entre 0 et 1, pour que les rapports des aires données soient cohérents.
Je serais curieux de savoir si quelqu'un y arrive, ou si c'est l'énoncé qui est fantaisiste.
#14 - 09-12-2018 18:48:49
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
La déécoupe du parallélogramme
Je ne vois pas où est le problème .
On construit les triangles 8 et 10 n'importe comment puis la zone 72 . Les directions (AB) et (BC) sont alors fixées . Il n'y a plus qu'à choisir D sur la parallèle à (AB) passant par la pointe basse du triangle 8 pour obtenir le point D et la zone 79 , le reste coule de source 
Vasimolo
#15 - 09-12-2018 20:26:50
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
La découpee du parallélogramme
@Vasimolo #14 :
Je suis d'accord jusqu'à la construction du point D.
Ensuite, je ne comprends pas pourquoi tu obtiens justement 79, et pourquoi les 3 droites sont concourantes en A.
#16 - 09-12-2018 21:23:48
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
La décooupe du parallélogramme
Je me suis moi aussi demandé si les valeurs données pour les aires pouvaient correspondre à un parallélogramme réel, et la réponse est assurément OUI.
Et je me suis demandé encore si ces valeurs conduisaient à un parallélogramme unique, dont on pourrait calculer les dimensions...  ? ?
Et si on pouvait aussi construire un autre parallélogramme en intervertissant par exemple les valeurs des aires de 10 et 72.
Cela conduirait alors à une valeur x = 143, pardon, 133  ! ? Cela impliquerait, bien évidemment, de modifier l'allure générale de la figure, tout en lui conservant sa topologie. ! ? Cela impliquerait, bien évidemment, de modifier l'allure générale de la figure, tout en lui conservant sa topologie.
Je pense posséder les réponses à ses questions, mais je vous laisse le loisir d'y réfléchir avant de vous les donner.
#17 - 09-12-2018 21:25:29
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
ka découpe du parallélogramme
Je ne suis d'accord ni avec Vasimolo, ni avec enigmatus. Je ne comprends pas la construction de Vasimolo, et pour enigmatus, il y a aussi la position de G sur [CD] qui compte, on n'a jamais dit que (BG)//(ED).
À part ça, oui, j'ai beaucoup d'amis, pourquoi ?
#18 - 09-12-2018 21:32:15
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
la décpupe du parallélogramme
C'est vrai, il n'a jamais été dit que (BG)//(ED).
Ce qui compte, encore une fois, c'est la topologie de la figure.
Il faut imaginer que les différents segments sont élastiques, et que tous les angles sont articulés  . .
#19 - 10-12-2018 18:06:19
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
la découpe du paeallélogramme
J'ai fini par me convaincre, avec difficulté, que Jackv avait raison (hormis sur le fait que x=143  ). J'arrive systématiquement à créer une figure avec les proportions attendues avec Geogebra, par une méthode d'essais et erreurs. Mais je serais bien en peine d'en tirer une démonstration propre, pour l'instant. ). J'arrive systématiquement à créer une figure avec les proportions attendues avec Geogebra, par une méthode d'essais et erreurs. Mais je serais bien en peine d'en tirer une démonstration propre, pour l'instant.
J'attends de voir la méthode de Jackv, des fois que ça clarifie des choses. Et même si c'est le cas, il reste bien des questions en suspens, comme... quelle est l'aire du parallélogramme ? Une bien belle question soulevée par enigmatus, on peut s'amuser un moment.
#20 - 10-12-2018 20:11:54
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
La découpe du paralléogramme
J'avais effectivement supposé à tort que BG était parallèle à ED.
Je n'arrive cependant pas à trouver une figure dont les aires en gris clair sont proportionnelles aux valeurs données.
#21 - 10-12-2018 23:24:50
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
la décoype du parallélogramme
Ebichu :
J'ai fini par me convaincre, avec difficulté, que Jackv avait raison (hormis sur le fait que x=143).
Tu as raison, je suis très mauvais en calcul mental  ! J'ai corrigé ! J'ai corrigé  . .
#22 - 11-12-2018 08:52:47
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
La découpe du parallélogrammme
Voilà, j'ai obtenu une solution approchée.
En existe-t-il d'autres ? Mystère pour l'instant.
Spoiler : [Afficher le message] Rectangle ABCD de forme quelconque, mais d'aire 359.44 (par exemple AB=26.8120 CD=13.4060)
AE/AB = 0.40960
CF/CB = 0.41608
CG/CD = 0.31896
A79 = 78.999215
A72 = 71.999971
A8 = 7.999978
A10 = 10.000835
? = 9.000101
On obtient d'autres solutions en décalant AB et CD d'une quantité arbitraire, mais en conservant leur distance.
#23 - 11-12-2018 10:19:12
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
la découpe du parallélogrammr
enigmatus :
En existe-t-il d'autres ? Mystère pour l'instant.
La réponse est OUI.
Spoiler : [Afficher le message] A mon avis, pas loin d'une infinité.
Il suffit pour en trouver d'autres, de modifier les dimensions du rectangle , tout en conservant son aire, quitte à en faire un carré ! Et là la solution devient unique  . .
#24 - 11-12-2018 10:55:36
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
La découp edu parallélogramme
@Jackv #23 :
C'est aussi ce que j'indique dans ma réponse en #22. Je me demandais s'il existait une série de solutions avec d'autres positions relatives de E, F, G.
#25 - 11-12-2018 22:30:00
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
La découpe du paralllogramme
Tu as raison. Je voulais dire qu'il y a une infinité de rectangles qui correspondent aux 4 valeurs imposées, à condition de respecter les bons rapports AE/AB, CF/CB et CG/CD.
On pouvait le deviner dès le départ : Le parallélogramme était défini par 5 paramètres (ou variables). Si on impose 4 aires (ou équations) le système n'est pa
|
 |

 Accueil
Accueil
 Forum
Forum








