Si X est impair (ou Y)
arrondi (X/2) * Y + (arrondi(X/2)-1)

Si X et Y sont pairs
(X * Y/2) + X/2

Arrondi par défaut, ça suffit, non ?
Merci pour la "correction" du premier cas, je n'arrivais pas à le faire simplement !

Pour le deuxième, je suis une buse car j'ai oublié de contrôler ma réponse. (j'ai la réponse graphique, mais j'ai planté la mise en équation)
(X * Y/2) + X/2 + (Y/2 - 1)

J'arrive à construire récursivement un serpent de taille [latex]\lfloor\frac{xy+x+y-1}{2}\rfloor[/latex], en me ramenant à un rectangle de x sur (y-2).

Il me reste à démontrer qu'on ne peut pas obtenir de serpent plus grand.

Il me semble que le résultat ne change pas si on autorise les hydres (des serpents avec plusieurs têtes), du moment qu'il n'y a pas de cycle.

Ok, tentons une démonstration, tolérant certaines libertés…

Je ne reviens pas sur le cas x=1,

Imaginons que notre serpent souffre d’obésité. Et qu’il soit large de non pas 1, mais 2 cases. Il se balade en restant centré sur une case, mais la pauv’ bête déborde d’1/2 case de chaque côté. Avec une autorisation de braquer en angle droit quand même, il souffre assez comme ça. Et il peut utiliser dans un passage retour les demi-cases latérales sur lesquelles il n’est pas passé à l’aller.

Notre ‘damier’ est étendu d’1/2 case tout autour, pour permettre à notre invertébré de cheminer partout. La surface du damier est donc de (x+1)(y+1).

Au mieux, notre ami pourra passer par la moitié de cette surface compte tenu de son embonpoint (si on oublie ses flans, bien entendu, pour revenir à notre problème initial). Soit (x+1)(y+1)/2 cases.

Seulement voilà, tout boucle étant interdite, il doit bien commencer quelque part et finir quelque part (comme le dit la chanson). Ce faisant, il va condamner 1/2 case au départ et 1/2 case à l’arrivée, celle derrière ou devant lui, inutilisables ensuite dans son parcours. Donc une case en tout en terme de surface.

Soit au mieux [(x+1)(y+1)-2]/2 cases parcourues finalement. Et comme il faut que tout ça soit un nombre entier, on revient au maximum à [(x+1)(y+1)-3]/2 si x et y sont pairs.

Il s’agit d’un maximum théorique, mais comme on peut aisément trouver une solution (et même plein) atteignant ce résultat, il a une belle tête de vainqueur.
La rigueur de tout ça est très relative, je sais.

J'ai trouvé une solution. Elle consiste à épaissir le serpent d'un demi-carreau de chaque côté, à la suite de quoi l'aire occupée par le serpent vaudra 2L+2, où L est la longueur du serpent. En voici la preuve.

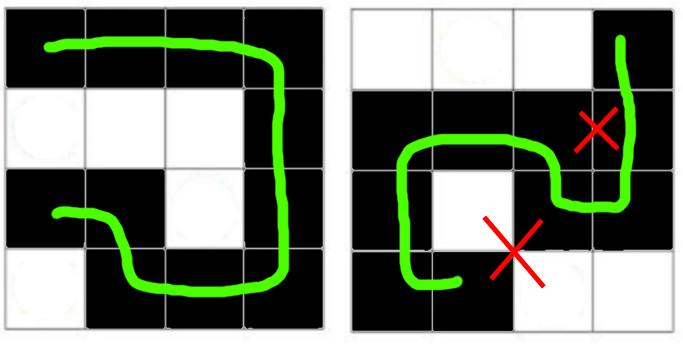
Pour un carreau sur lequel le serpent voyage en ligne droite, on rajoute deux petits carrés de côté 1/2 carreau (verts) de chaque côté du serpent (cas du milieu sur mon illustration).



Si le serpent fait un virage (cas de gauche), on rajoute cinq petits carrés verts, mais on enlève un petit carré à l'endroit en rouge, car les petits carrés verts des deux carreaux voisins du virage vont se chevaucher à cet endroit.

Si enfin on est à une extrémité du serpent (cas de droite), on rajoute 8 petits carrés verts.

Chaque extrémité contribue pour 3 carreaux, et chaque virage ou chaque ligne droite pour 2 carreaux chacun. Un serpent de longueur L recouvre ainsi une aire totale de 2L+2.

Considérons le rectangle initial de taille xy, et agrandissons-le de 1/2 carreau le long de chaque bord, de sorte qu'on a maintenant un rectangle d'aire (x+1)(y+1). Le serpent épaissi va recouvrir une partie de cet rectangle.  On a donc 2L+2 <= (x+1)(y+1) d'où [latex]L \leq \frac{xy+x+y-1}{2}[/latex].

L'hydre n'est guère plus compliqué. Quand on a un T, ça rajoute une extrémité au serpent, et il faut placer à côté de la case du T deux petits carrés verts et deux petits carrés rouges. Quand on a un +, ça rajoute deux extrémités au serpent, et il faut placer 4 petits carrés rouges à côté de la case du +. La même démonstration tient.

Pour la question ouverte, j'adopte la même démarche, sauf qu'au lieu d'épaissir mon serpent régulièrement, je lui rajoute des pointes : sur chaque côté de longueur 1 carreau bordant le serpent, je rajoute une pointe formée d'un triangle rectangle isocèle, dont l'hypoténuse est le côté de longueur 1 (un tel triangle a donc une aire de 1/4 carreau). J'obtiens un majorant de la taille du serpent : [latex]\lfloor\frac{2xy+x+y-1}{3}\rfloor[/latex].

Il n'est pas optimal, par exemple pour un rectangle 4x2, il donne 7, alors que le plus grand serpent possible est de taille 6. Par contre, il donne parfois la bonne valeur, comme pour le rectangle 6x3 où il donne 14.

Pour le problème ouvert, Ebichu obtient une borne supérieure de :
[TeX]\left \lfloor \dfrac{2xy+x+y-1}{3} \right \rfloor[/TeX]
Pour ma part, j'arrive à obtenir:
[TeX]\left \lfloor \dfrac{15xy+8x+8y+4}{24} \right \rfloor[/TeX]
Qui dit mieux?

Indice:
Spoiler : [Afficher le message] Cherchez longueur plutôt qu'aire, c'est plus simple

J'ajoute aussi un indice pour ceux qui ne décollent pas sur la première question

Spoiler : [Afficher le message] intérieur et extérieur se complètent

Franky1103
Oui, c'est la bonne formule, une démo?

Non, la formule donnée, c'est pour la deuxième question, avec les coins qui se touchent. Pour le problème de l'hydre, il faut montrer que l'on obtient la même chose qu'avec un serpent...

Ce n'est pas une démonstration, c'est une conjecture.
Ou alors si pour chaque x,y, tu as trouvé un serpent avec la taille que tu indiques, alors tu as démontré que c'était une borne inférieure.
Il reste à démontrer que l'on ne peut pas trouver de serpents plus grand que cette borne, et c'est généralement pas la partie la plus simple dans ce genre de problème...

Les réponses sont désormais visibles, voici ma méthode. Plutôt que de passer par une aire autour du serpent, je passe par le périmètre du serpent.

Le périmètre du serpent est égal au périmètre autour des cases blanches et du bord.

Le périmètre du serpent est 2n + 2, ou n est le nombre de case noire. En effet, une case noire à un périmètre de 4.
Chaque case noire ajoutée possède exactement un bord en commun avec le reste du serpent déjà construit (pas de cycle, ce qui est commun avec le problème de l'hydre)

Soit m le nombre de cases blanches.
Le périmètre du rectangle est 2x + 2y. On a m + n = xy (aire du rectangle)
Toutes les cases blanches se rattachent au bord (via une succession de cases blanches. En effet, si un groupe de cases blanches n'était pas rattaché au bord, il serait entouré de cases noires. Or les cases noires ne peuvent former de cycles.
On peut donc de proche en proche ajouter des cases blanches de manière à ce qu'elles soient en contact avec un bord du rectangle ou avec une case blanche déjà posée. A la différence des cases noires, les cases blanches ajoutées peuvent toucher plusieurs autres cases blanches. A chaque case blanche ajoutée, le périmètre augmente de 4 - 2*c ou c est le nombre de contact de la case blanche avec les cellules préalablement posée. Comme c >= 1, le périmètre augmente au maximum de 2. Le périmètre est donc inférieur à 2x + 2y + 2m.

Donc par égalité des périmètres noirs et blancs, on a [latex]2n + 2 \leq 2x + 2y + 2m[/latex]
soit [latex]4n + 2 \leq 2x + 2y + 2m + 2n = 2x + 2y + 2xy[/latex]
Ou encore [latex]n \leq \dfrac{x + y + xy -1}{2}[/latex]
Comme n est entier, on a [latex]n \leq \left \lfloor\dfrac{x + y + xy -1}{2}\right \rfloor[/latex]
Il est facile de vérifier que cette borne est atteinte.

Dans le cas d'un serpent touchant les coins, les cases blanches ajoutées peuvent ne toucher aucune case précédemment posée. Dans ce cas, le périmètre blanc sera inférieur à 2x + 2y + 4m.
On en déduit le majorant d'Ebichu, mais on s'aperçoit vite que cette borne n'est pas atteinte souvent.

On peut toutefois améliorer un peu...
Le périmètres blanc est égal à 2x + 2y + 4m - 2c, ou c est le nombre total de contacts entre 2 carrés blanc ou entre un carré blanc et le bord du rectangle. Pour que c = 0, il faudrait que toutes les cases autour du rectangle soit noires. Déjà, cela ferait un cycle, ce qui donne c > 0. Mais surtout, toutes les cases adjacentes au cases noires au bord du rectangle seraient blanches, ce qui augmenterait beaucoup le nombre de contacts.

Ainsi, on voit que si il y a 4 cases noires adjacentes le long du bord, alors au moins deux cases blanches sont en contact à cet endroit.

Soit B et N le nombre de cases blanches et noires sur le bord. B + N = 2x + 2y - 4 = L.
Si B cases blanches sont en contact avec le bord, alors cela implique que N - 3B-8 cases blanches sont en contact sur le deuxième anneau (après analyse des coins). Si B > (xy - 12)/4, alors, il y a au moins (L - 8)/4 contacts sur le bord. Sinon, il y a B + N - 3B - 8 = L - 3B - 8 > (L - 8)/4 (car c'est minimal si B est maximal).
Il y a donc au moins (L - 8)/4 contacts, donc le périmètre blanc est inférieur à:
2x + 2y + m - (L - 12)/2 = (4x + 4y + 4m - 2x - 2y + 4 + 8)/2 = (2x + 2y + 4m + 12)/2.
On obtient alors [latex]\left \lfloor \dfrac{8xy+2x+2y+8}{12} \right \rfloor[/latex]
(Je ne sais pas d'où sortait mon 6, sans doute encore une erreur...)

Exact, on peut diviser par 2...

Oui, les deux premières formules sont évidemment fausses, asymptotiquement, un serpent maximal occupe les 2/3 de l'aire totale.

J'ai oublié d'indiquer où j'ai trouvé le problème:
http://depot-e.uqtr.ca/7700/1/031015002.pdf
(voir les 12 dernières pages)
Il donne les conjectures pour les serpents maximaux.
Je pense que le problème n'est actuellement pas si compliqué à résoudre. En utilisant ce que j'ai fait pour améliorer  la borne supérieure, mais en l'appliquant sur un anneau plus grand, je pense que ça doit marcher. (Mais il faut appliquer sur un anneau d'au moins 5 cases normalement). Il faut aussi bien prendre en compte les coins et les deux extrémités du serpent. Ça me parait très fastidieux, mais faisable (en faisant une grosse récurrence en peu dégueu sur l'arrangement optimal sur tout le bord)