Enigme Une simplification bien embarrassante... @ Prise2Tete

Oups! · #1

... ou De l'art de compliquer les choses "triviales"

Voici un petit problème original je l'espère (dans le sens où c'est pure invention)

Sur un snooker dont la surface de jeu fait 2,54 m x 1,27 m se trouvent 2 billes au même endroit (point A) distant de 0.34 m de la bande (a). Spoiler : [Afficher le message]
N'étant pas manchot, je parvient d'un seul coup, sans mettre d'effet, à faire rentrer les deux billes dans les deux poches les plus éloignées.

QUESTION : à quelle distance (b) du bord de la table les trajectoires des billes se sont-elles (re)croisées ?

vous-avez 20 minutes je ramasse les copies.

JJ

halloduda · #2

Dommage, ça ne fait pas un compte rond.

Les trajectoires partent des symétriques de A par rapport aux deux bords.
La distance entre ces deux points est le double de la largeur de la table, soit 254 cm.
Le point de croisement est au tiers à partir de la bande du fond.

Par exemple à partir de la bande de gauche, la distance b est [latex]\frac2 3.(254-34)-(127-34)[/latex]
= 53.667 cm

J'ai dépassé les 20 minutes, c'était la rédaction.

L00ping007 · #3

b=0,73333 ?

looozer · #4

Soit A' et A'' les symétriques de A par rapport aux deux bords du billard.
A'A''=2,54 ; MN=1,27
[MN] est donc l'image de [A'A''] par une homothétie de rapport -1/2 centrée en B.
B est donc à 1/3 de [MA'].
En utilisant Thalès, j'en déduis que HB vaut aussi 1/3 de PA', c'est-à-dire (a+1,27)/3

Oups! · #5

Tout d'abord désolé, je pensais intervenir plus tôt.
Ensuite, merci, cela fait un sacré moment que j'essaie en vain de résoudre ce problème de manière géométrique sans y parvenir *

Et pourtant je savais qu'ils fallait s'aider de Spoiler : [Afficher le message] ~~ce Monsieur bien connu~~ THALES mais je m'y suis mal pris...

Cette énigme est une transposition figurative d'une autre énigme que j'avais cru — sot que je suis — rendre plus aisée à résoudre par cette artifice géométrique.
* Finalement, j'ai résolu l'énigme en question de façon plus conventionnelle, ce qui fait que d'une certaine manière, j'avais la solution... indirectement.

pour halloduda et looozer (joli dessin en passant), Si vous êtes curieux, l'énigme est ici:
~~http://www.prise2tete.fr/upload/Oups!-EnigmeEE.DDD.txt~~
cf. message #9

Non looping, ce n'est pas ça...

kosmogol, ça va mieux maintenant ?

JJ

L00ping007 · #6

J'ai refait mes calculs, et je tombe à nouveau sur cette formule :
[TeX]b=\frac{2L-a}3[/TeX]
où L est la largeur du billard.
Et ça fait b=0,733...

Je déplie mon billard en 3, un à droite, un à gauche, et j'en décale un des 2 pour faire apparaître les bons triangle. Le reste c'est du Thalès (ou des tangentes).

Où est mon erreur ?

EDIT

Ok j'ai compris, j'ai la longueur symétrique par rapport à la largeur du billard.

La réponse est donc [latex]b=\frac{L+a}3\approx 0,53666...[/latex]

Jackv · #7

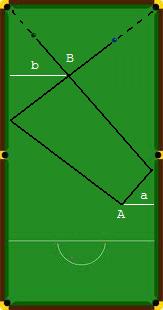
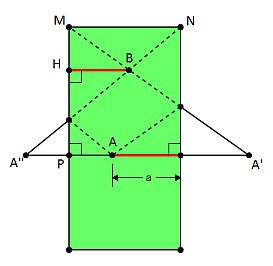
Il suffit de prendre le symétrique du point A par rapport au deux bords droit et gauche pour obtenir 2 fois 2 triangles semblables pour lesquels on peut écrire les relations (en cm) :
(127+34)/b = (2*127-34) / (127-b)
161*127=(220+161) * b

b = 68,034 cm

scarta · #8

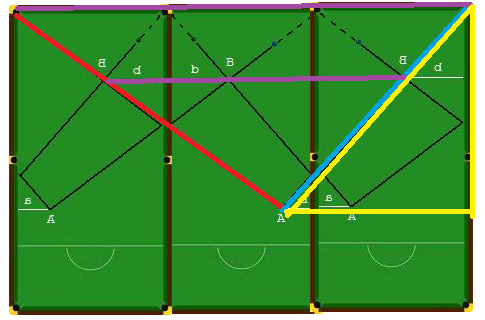
Comme l'avait fait remarquer Vasimolo lors de toute sa série "Billard", on peut généralement simplifier les problèmes en accolant des billards symétriques les uns aux autres.
Ici, si on accole 2 autres billards à droite et à gauche comme ceci, on peut simplifier les trajectoires en "rouge" et en "bleu".
On remarque alors que les 2 droites violettes font 2L et 3L (L étant la largeur du billard). Le 2L est obtenu en faisant b + L + L-b
D'après le théorème de Thales, on retrouve ces rapports de 2/3 sur les droites rouge et bleue.
Considérons donc le triangle jaune : toujours d'après Thalès b/(L+a) = 1/3
De là, il découle que b = (L+a)/3
Application numérique: b = (1.27 + 0.34) / 3 = 0.54

Oups! · #9

Bravo à tous, un sans faute, enfin, sauf pour jackv, bête erreur dans le calcul (161*127 / (220+161) = 53.667)

Cette énigme est une transposition figurative d'une autre énigme que j'avais cru rendre plus aisée à résoudre par cette artifice géométrique :

"Au même moment, un véhicule part du point A pour se rendre au point B tandis qu'un second véhicule par du point B pour aller au point A. Ils se croisent à à 3 km du point de départ de l'un d'eux.
Chacun, un fois à destination, y reste pendant 2h30 avant de prendre le chemin du retour. Ils gardent la même vitesse (que l'on considérera constante) qu'à l'aller. Ils se croisent à nouveau à 2 km de l'un des points de départ.

Quelle est la distance A-B ?"

Au départ, j'avais schématisé cela sous la forme de droites symbolisant les parcours des 2 véhicules.
La figure géométrique obtenue ressemblait au dessin de looozer mais à l'envers et sans les prolongations des points A' et A''. Les trajectoires partant de M et N et se recoupant en deux points (B puis A) (note : le temps d'attente de 2h30 pouvant être réduit à 0).

JJ

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 25-03-2011 14:55:56

Une simpliication bien embarrassante...

#0 Pub

#2 - 25-03-2011 15:19:51

Une implification bien embarrassante...

#3 - 25-03-2011 15:46:11

Une simplificatiion bien embarrassante...

#4 - 25-03-2011 17:13:01

Une simplification bien embarrassnate...

#5 - 26-03-2011 18:22:24

une simplification bien elbarrassante...

#6 - 26-03-2011 18:36:24

une simplification bien embarrassznte...

#7 - 28-03-2011 23:12:02

Une simplification bien embarrasante...

#8 - 29-03-2011 09:08:30

Une simplification bien embaarrassante...

#9 - 01-04-2011 13:42:29

ine simplification bien embarrassante...

Réponse rapide

Sujets similaires

Mots clés des moteurs de recherche

Pied de page des forums